 |
Виды несимметричных коротких замыканий
|
|
|
|
Принято рассматривать три основных вида несимметричных коротких замыканий К(1), К(2) и К(1.1), см. табл. 1. Для расчетов и сравнения тяжести коротких замыканий в зависимости от их вида считают, что несимметричное замыкание является глухим (то есть полагают, что сопротивление дуги равно нулю, rд = 0). Расчетные формулы токов и напряжений для симметричных составляющих легко могут быть распространены и на случаи rд 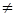 0.
0.
Схемы коротких замыканий, которые используются для получения расчетных формул, приведены на рис. 5.1.
 Рис. 5.1
Рис. 5.1
Как можно видеть, точку несимметричного короткого замыкания располагают как бы на ответвлении в месте КЗ. Токи в ответвлении условно направлены к точке КЗ - это токи фаз I KA, I KB, I KC.
На схеме замещения точку КЗ изображают для симметричных составляющих так, как показано на рис. 5.2.
Токи I 1л, I 2л, I ол представляют собой симметричные составляющие прямой, обратной и нулевой последовательностей в ветви слева от точки «а», токи I 1п, I 2п, I оп – соответствующие токи правой от точки «а» ветви. Расчет токов последовательностей ведется для фазы А, токи других фаз определяются через ток фазы А. Для схем замыкания видов К(1), К(2) и К(1.1), см. рис. 5.1, достаточно определить ток прямой последовательности в точке короткого замыкания, чтобы затем через него найти токи обратной и нулевой последовательностей в этой точке.

Рис. 5.2
Расчетные формулы и соотношения для токов симметричных составляющих в месте короткого замыкания приведены в табл. 1. На рис. 5.3 представлены: схема простейшей передачи (а), в цепи которой в точке,, а '' происходит несимметричное короткое замыкание; схемы замещения прямой (б), обратной (в) и нулевой (г) последовательностей.
|
|
|

Рис. 5.3
В табл. 2: ЭДС ЕАΣ – эквивалентная ЭДС источников Е и U прямой последовательности относительно места КЗ, то есть точек К – К` (для схемы рис. 5.3):
 (5.1)
(5.1)
X 1Σ – результирующее сопротивление схемы прямой последовательности относительно точек К – К`:
 (5.2)
(5.2)
В схемах замещения обратной и нулевой последовательностей нет соответствующих источников ЭДС. Сопротивления схем Х 2Σ и Х 0Σ относительно места КЗ, применительно к схемам рис. 5.3, в, г, определяются по формулам:

 (5.3)
(5.3)
Т а б л и ц а 2
Токи в месте КЗ
(обозначения)
Вид короткого замыкания

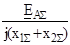


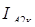
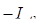
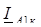






 (5.4)
(5.4)