Моделирование основных химико-технологических процессов переработки полимеров.

— Химико-технологические процессы переработки полимеров достаточно разнообразны, но можно выделить три стадии переработки полимеров: смешение, формование и отверждение (вулканизация). В ряде случаев те или иные процессы могут отсутствовать или, наоборот, присутствовать какие-то неуказанные (например, подготовка сырья), все-таки эти три стадии следует считать определяющими.

Смешение.

5.1.1. Общие сведения.

— В большинстве случаев чистые полимеры не обладают нужным комплексом свойств и не могут быть использованы для изготовления изделий. В ряде случаев, например, в производстве резин, чистый полимер вообще невозможно превратить в пригодные для эксплуатации изделия, не введя в него предварительно целого ряда дополнительных ингредиентов.

— Основное требование, которое предъявляется к любой полимерной композиции, – это высокая однородность всех физических и химических характеристик. Поскольку все характеристики композиции определяются ее составом, такая однородность свойств достигается только при равномерном распределении компонентов в объеме полимера. Поэтому основное содержание процесса смешения можно определить так: смешение – это процесс, целью которого является превращение исходной системы, характеризующейся упорядоченным распределением ингредиентов, в систему, характеризующуюся неупорядоченным, статистически случайным распределением.

— Обычно какие-то из компонентов вводятся в виде более или менее крупных кусков или агломератов. Поэтому процесс смешения сопровождается одновременным измельчением (диспергированием) этого компонента.

— Основные этапы смешения. Смешение можно представить как сумму двух процессов: 1) простое смешение (гомогенизация), заключающееся в равномерном распределении ингредиентов в общем объеме; 2) диспергирующее смешение, приводящее к разрушению комков и агрегатов ингредиентов до частиц меньших размеров. Фактически оба процесса идут одновременно, поскольку механическое воздействие на систему обязательно приводит к дроблению агрегатов, однако преобладание одного из них зависит от условий смешения, в частности от скоростей и напряжений, возникающих в системе.

— Смешение происходит за счет сдвига слоев материала относительно друг друга по приведенной схеме.

— В соответствии с этой схемой деформация сдвига между двумя параллельными плоскостями выражается безразмерной величиной g=l/h. Скорость сдвига определяется величиной деформации в единицу времени t: g'=l/(ht) и характеризует интенсивность простого смешения, обусловленного для приведенного случая уменьшением толщины слоев и ростом площади их соприкосновения.

— Интенсивность диспергирующего смешения зависит от вязкости системы, поскольку разрушение агломератов происходит тогда, когда когда силы внешнего трения в вязкой среде превышают силы сцепления отдельных частиц в агломерате. При диспергирующем смешении разрушающие деформации невелики, что позволяет использовать в этом случае закон Ньютона t=m×g' или t=m_эф×(g)ⁿ. 'Для ускорения диспергтрующего смешения необходимо повышать напряжение сдвига в системе.

— Скорость и напряжение сдвига являются основой для количественного описания процесса смешения. Интенсивность простого смешения можно определить по величине суммарной (накопленной) деформации сдвига через среднюю скорость сдвига и длительность сдвига. При простом смешении происходит также диспергирование ингредиентов, поэтому g_S может служить мерой качества приготовления композиции.

— Диспергирующее смешение рассчитывают по общей работе, совершенной внешней силой при смешении (А_S) и расходуемой на накопление в виде упругой энергии (А₀), диспергирование частиц (А_D) и повышение интенсивности рассеяния энергии (W): А_S=А₀+А_D+W.

Принимают, что

;

;

.

Здесь t_c(t), t_p(t) – текущие значения напряжений сдвига в системе полимер–наполнитель и в полимере; t_с0 и t_р0 – соответствующие им равновесные значения напряжения сдвига; t – время деформирования. Принимая W»0, можно рассчитать работу диспергирования:

.

Например, для каучуков, наполненных техническим углеродом, получено соотношение: А_D=kА_S (коэффициент k <0.2).

1 – холостой ход; 2 – измельчение полимера и кусковых материалов; 3 – уплотнение и смачивание порошкообразных ингредиентов; 4 – диспергирование наполнителей; 5 – гомогенизация смеси, пластикация полимера; I – разделение; II – диспергирование; III – пластикация; IV – простое смешение.

— Это подтверждается анализом зависимости потребляемой мощности на различных этапах от продолжительности смешения (зависимость получена при смешении каучука с техническим углеродом в роторном смесителе).

Загружаемые в смеситель полимер и кусковые материалы измельчаются (зона 2), на что затрачивается малая энергия. Ее потребление резко возрастает после создания в смесителе прессующего давления, которое совместно с вращающимися роторами уплотняет находящуюся в камере рыхлую смесь и одновременно способствует интенсификации внедрения наполнителей в полимер (зона 3). При этом параллельно идут два процесса: уплотнение, преобладающее в начале прессования, и смачивание порошкообразных материалов полимером и жидкими ингредиентами. Энергия уплотнения и смачивания велика, поэтому в смесителе повышается температура, полимер переходит в вязкотекучее состояние. Это обусловливает снижение его вязкости, более быстрое смачивание порошков и приводит к образованию относительно плотной монолитной части смеси, в которой появляются сдвиговые напряжения, начинает реализовываться диспергирующее смешение (зона 4), идет пластикация полимера и гомогенизация (зона 5). Однако поскольку в системе имеется свободный наполнитель, процессы смачивания, диспергирования, пластикации и гомогенизации протекают одновременно. Интенсивность лиспергирующего смешения (и соответствующая ей зависимость потребления энергии) меняется по кривой с максимумом, т.к. вначале в смеси мало несмоченного наполнителя. При возрастании степени смачивания темпы снижения вязкости полимера вследствие роста температуры становятся выше темпов возрастания вязкости смеси из-за внедренного наполнителя, что приводит к замедлению и прекращению процесса диспергирования. В конце цикла смешения происходит деструкция (пластикация) полимера и усреднение, гомогенизация системы.

На стадии I происходит процесс разделения, увеличивается уровень деформаций, повышается поверхность раздела фаз, возрастает плотность, происходит смешение полимера с агломератами наполнителя. Деформированные слои полимера обволакивают агломераты, изолируя их друг от друга (возрастает электрическое сопротивление слоя, что дает представление о том, на какой стадии находится процесс смешения). На стадии II наблюдается прогрессирующее уменьшение размера частиц наполнителей (электрическое сопротивление слоя падает, поскольку изолирующая прослойка разрушается). На стадии III наблюдается изменение реологических свойств, уменьшается вязкость из-за механо-химической деструкции. Стадия IV имеет место в течение всего процесса смешения т состоит в перемещении компонентов через массу без изменения их формы и размеров.

— Статистические закономерности смешения. Основной целью любого смешения является максимальное увеличение поверхности раздела между смешиваемыми компонентами

— Поверхность раздела возрастает при диспергировании. Рассмотрим шарообразную твердую частицу наполнителя диаметром D, объемом V=pD³/6. Поверхность такой частицы S=pD². После диспергирования этой большой частицы мы получаем n маленьких диаметром d (объем их, естественно, не изменяется). Поверхность этих частиц S'=npd². Из неизменности объемов вытекает: pD³=npd³. d=D/n^1/3; d²=D²/n^2/3; S'=Sn^1/3. Отклонение от шарообразной формы ведет к еще большему возрастанию поверхности раздела.

— Поверхность раздела возрастает за счет деформации растяжения. Рассмотрим твердую частицу наполнителя в виде куба со стороной а объемом V=а³. Поверхность такой частицы S=6а². После деформации куба мы получаем параллелепипед длиной b, поперечное сечение которого представляет собой квадрат со стороной а/k. Объем параллелепипеда а²b/k² равен объему куба. Отсюда b=ak². Поверхность параллелепипеда S'=2a²/k²+4a/k=S×p, где p=(1+2k³)3k². Покажем, что р>1. Для этого решим неравенство 2k³–3k²+1>0; k>1. f(k)=2k³–3k²+1; f'(k)=6k²–6k; f"(k)=12k–6; Составим традиционную схему исследования функций.

k	<0		(0; 1)		>1
f'(k)	+		–		+
f(k)	растет	1 (max)	падает	0 (min)	растет
f"(k)		–		+

При k>1 p>1.

— Из приведенной выше схемы смешения слоев материала относительно друг друга за счет сдвига мы можем видеть, что при сдвиге сечение слоя уменьшается, а длина его возрастает. Это эквивалентно по своим результатам реализации деформации растяжения.

— Поскольку поверхность раздела увеличивается вследствие деформации сдвига, которая, в свою очередь, определяется уровнем напряжений сдвига и реологическими характеристиками среды, интенсивность перемешивания сильно зависит от соотношения вязкостей диспергируемой фазы и дисперсионной среды. Если вязкость диспергируемой фазы намного превышает вязкость дисперсионной среды, то, несмотря на возможность значительных деформаций сдвига последней, диспергируемая фаза практически почти не будет деформироваться.

— Для иллюстрации этого положения рассмотрим простейшую схему процесса ламинарного смешения, при которой смешиваемые компоненты расположены слоями между тремя параллельными плоскостями. Слой А – дисперсионная среда с вязкостью h₁; слой Б – диспергируемая фаза с вязкостью h₂; слой В – снова дисперсионная среда с вязкостью h₁. Расстояние между плоскостями Н; толщина слоя дисперсионной среды h.

Представим, что верхняя плоскость движется с постоянной скоростью V, а нижняя неподвижна; в этом случае во всех трех слоях устанавливаются одинаковые напряжения сдвига, значения которых определяются соотношениями t=h₁g'_А=h₂g'_Б=h₁g'_В, где g'_А, g'_Б и g'_В – значения скорости сдвига в каждом из слоев. Скорость сдвига в каждом слое определяется как отношение разности скоростей на его границах к толщине слоя: g'_А=(V_А–V_Б)/h; g'_Б=(V_Б–V_А)/(H–2h); g'_В=V_В/h Þ V_В = g'_Вh. Поскольку g'_А=g'_Б Þ V_А–V_Б=V_В и V_Б=V_А–V_В. Тогда g'_Б=(V_А–2V_В)/(H–2h) и g'_Б=(V_А–2g'_Вh)/(H–2h. Так как g'_В=g'_Б×h₂/h₁ и V_А=V, получим:

,

,

.

Следовательно, если вязкость дисперсионной среды мала (или велика вязкость диспергируемой фазы), отношение h₂/h₁ становится очень большим, в то время как g'_Б оказывается мало, стремясь к нулю по мере увеличения отношения h₂/h₁. Напротив, если вязкость дисперсионной среды много больше, чем вязкость диспергируемой фазы, то отношение h₂/h₁ стремится к нулю, и предельное значение скорости сдвига в диспергируемой фазе g'_В=V/(H–2h). Поэтому целесообразно проводить смешение, добавляя менее вязкий компонент к более вязкому.

— Вернемся к статистическим закономерностям смешения.

— Действительный характер распределения вещества А в объеме смеси зависит от множества трудноучитываемых факторов, поэтому целесообразно считать этот процесс стохастическим и применять для его описания статистические закономерности. Примем, что при смешении приращение площади поверхности раздела за отрезок времени dt прямо пропорционален разности между максимально возможным и текущим значением межфазной поверхности. При этом тип смешения (простое или диспергирующее) в дальнейшем оговаривать не будем, так как с этой точки зрения совершенно безразлично состоит ли заранее фаза А из отдельных частиц (простое смешение) или они образуются при дроблении вещества А в системе (диспергирующее смешение).

На основании принятого допущения можно записать: dS/dt=K(S*–S), где dS – приращение площади раздела (межфазной поверхности) за время dt; S и S* – текущее и предельное значение площади поверхности раздела, соответственно; K – коэффициент пропорциональности. Решение этого дифференциального уравнения при начальном условии: S=S₀ при t=0, имеет вид: S=S*–(S*–S₀)exp(–Kt). На практике почти всегда S*»S₀, поэтому S=S*(1–exp(–Kt)). Вероятность P попадания в случайно выбранный объем загрузки по крайней мере одного элемента межфазной поверхности выражается формулой: . Подставляя сюда выражение для S, получаем: . Здесь под вероятностью Р следует понимать отношение числа элементарных объемов, содержащих по крайней мере один элемент поверхности раздела, к общему числу элементарных объемов смеси.

— Разделим все количество вещества А на n достаточно малых равных порций произвольной величины. Тогда объем смеси v, приходящийся на одну порцию вещества А, будет равен: v=V/n. Если взять пробы смеси объемом V₀, то вероятность отсутствия вещества А в любой части объема V₀ будет равной . Вероятность отсутствия компонента в объеме v определится соотношением . Z=v/V₀. Тогда вероятность P_v отсутствия по крайней мере одной порции вещества А в каждом объеме v пробы с объемом V₀ определяется равенством: . Величину P_v следует считать равной отношению объемов v, содержащих по крайней мере одну порцию вещества А, к общему числу объемов v в объеме V смеси.

— Приведенные здесь выражения позволяют определить время смешения, необходимое для достижения заданной степени распределения компонента А. Необходимое качество смешения определяется заданием величины P_v, т.е. отношением количества объемов v, содержащих не менее m ед. массы вещества А, к общему числу объемов v в объеме смеси. Величина P_v имеет смысл доверительной вероятности получения смеси данного качества. Поэтому качество смешения можно считать удовлетворительным при P_v =0.90¸0.95 и хорошим при P_v >0.95.

— Значение объема v можно брать соответствующим случаю теоретически равномерного распределения компонента А в объеме смеси. Если теоретическая концентрация распределяемого вещества равна q ед. массы/ед. объема, то v=m/q, где m – масса компонента А в объеме v. При этом m следует брать произвольно, но так, чтобы объем v как можно отличался от объема проб V₀. Если принять v=V₀, то m=V₀q.

— В рассмотренные выше уравнения входят четыре неизвестных величины P, K, K₁×S* и t. Поэтому для расчета времени смешения необходимо использовать данные анализа двух серий проб смеси, отобранных через время t₁ и t₂ от начала смешения. Объемы проб в каждой серии должны быть равны V₀. Для каждой серии должны быть подсчитаны отношения Р₁ и Р₂ числа проб, содержащих не менее m ед. массы вещества А, к общему числу проб.

— На этом основании можно записать: и . Пусть, например, t₂=2t₁. Тогда: ; и, наконец: .

— Существующие методы количественного контроля однородности смеси после смешения базируются на статистическом анализе, основанном на сравнении теоретической дисперсии с фактическим значением среднеквадратичного отклонения концентраций диспергируемого вещества.

Теоретически показано, что разброс значений концентрации подчиняется биномиальному закону распределения. Это означает, что вероятность Р присутствия в отобранной пробе b частиц диспергируемой фазы равна плотности биномиального распределения: , где N – число частиц распределяемой фазы, содержащихся в пробе; b – число частиц диспергируемой фазы в пробе; q – теоретическое содержание диспергируемой фазы, равное отношению массы диспергируемой фазы к массе всей смеси.

В этом случае теоретическая дисперсия распределения s² определяется по формуле: s²=q(1–q)/N. Величина выборочной дисперсии концентрации диспергируемой фазы в отобранных пробах рассчитывается по уравнению: , . Здесь n – число проб; x_i – концентрация частиц диспергируемой фазы в i -ой пробе; – среднее арифметическое значение доли частиц диспергируемой фазы в смеси для n проб.

— Определение качества смеси сводится к сравнению экспериментально определенной дисперсии S² с теоретической s². При этом используется критерий J=s²/S², называемый индексом смешения. При увеличении однородности смеси индекс смешения стремится к предельному значению J=1.

— Качество смешения можно оценить коэффициентом неоднородности (в %) , где c_i – концентрация одного из компонентов в пробах; с₀ – концентрация этого же компонента при идеальном распределении; n_i – число проб с концентрацией c_i; n – общее число проб. Значение К_с=0 соответствует идеально смешанной системе.

В условиях заводских лабораторий определение качества смешения можно производить микроскопическим способом. В результате анализа определяют содержание компонента, его распределение в объеме смеси и распределение размера частиц компонента.

— Качество смешения можно оценивать еще химическим методом количественного анализа (весовым или объемным), электрохимическим методом, методом, основанным на измерении электропроводности, спектральными методами, ультразвуковыми методами, с помощью микрорадиоволн.

5.1.2. Смешение на вальцах.

— Здесь мы будем рассматривать, преимущественно, течение материала между двумя цилиндрическими поверхностями.

— Рассмотрим движение полимера в зоне между двумя вращающимися валками (цилиндрическими поверхностями). Будем исходить из того, что вследствие прилипания наружный слой материала движется вместе с поверхностью валка. Из-за наличия сил внутреннего трения наружный слой увлекает прилегающие к нему слои, и вся масса материала начинает втягиваться в зазор.

Поскольку площадь поперечного сечения зазора по мере удаления от входного сечения все время уменьшается, а обрабатываемый материал практически несжимаем, скорости движения слоев материала, расположенных на разных расстояниях от поверхности валка, оказывается различными. Всю рабочую зону можно разделить на две области: область А, в пределах которой центральная часть потока движется в направлении, противоположном направлению движению вилков, и область В, в которой весь находящийся в зазоре материал движется в одном направлении, однако при этом скорость движения материала по мере удаления от поверхности валка увеличивается.

Существование переменной по расстоянию скорости приводит к возникновению в транспортируемом через зазор материале деформации сдвига. При этом скорость деформации зависит от величины зазора, увеличиваясь с его уменьшением, так и от окружной скорости, увеличиваясь с ее возрастанием.

Поскольку скорость сдвига однозначно связана с напряжением сдвига, в различных точках находящегося в зазоре материала действуют разные напряжения сдвига, абсолютное значение и направлениекоторых меняется в зависимости от места расположения и режима (скорость, зазор, температура). Таким образом, материал, проходящий через зазор вальцов подвергается воздействию напряжений сдвига и претерпевает существенные по величине деформации сдвига,. При этом материал,. находящийся в области А, участвует как в поступательном, так и в циркуляционном движении. Существование области циркуляционного течения и областей с различной ориентацией скорости сдвига и обусловливает возможность применения вальцов для смешения. Смешение происходит в зазоре вальцов вследствие того, что материал подвергается большим сдвиговым деформациям, которым сопутствует периодическая переориентация расположения поверхностей раздела вследствие циркуляционного течения в области А и существования областей разноориентированных деформаций сдвига.

Для более эффективного смешения применяют вальцы с фрикцией, наличие которой интенсифицирует циркуляционное течение в области А. Так как перемешивание материала происходит только в плоскости, нормальной к оси валков, для выравнивания продольного распределения концентраций смешиваемых ингредиентов вальцуемый материал периодически снимается с поверхности валка, скручивается в рулон, который поворачивается на 90°, и затем вновь пропускается в зазор между валками. Таким образом достигается переориентация смешиваемого полимера относительно направления деформации. Дальнейшее вальцевание обеспечивает выравнивание концентраций в направлении, которое не охватывалось в предыдущем цикле.

Возникновение в проходящем через зазор материале значительных напряжений сдвига позволяет кроме смешения осуществлять при вальцевании и операцию диспергирования. Вследствие этого вальцевание используют не только для смешения, но и для диспергирования в полимере твердых и жидких ингредиентов. Поскольку процесс диспергирования происходит тем интенсивнее, чем больше напряжение сдвига, а уровень напряжений сдвига в свою очередь однозначно определяется значением эффективной вязкости, диспергирующее вальцевание следует вести при минимально возможных температурах, так как при этом вязкость, а, следовательно, и напряжение сдвига, максимальны.

Описанные выше изменения в характере течения материала, находящегося в зазоре, проявляются в изменении гидростатического давления. Из сопоставления поля скоростей с эпюрой давления следует, что трансформация поля скоростей сопровождается увеличением давления, достигающим в какой-то точке максимума. Такая форма профиля скоростей показывает, что силы, возникающие вследствие гидростатического давления и действующие с одной.сторону сечения, полностью уравновешиваются аналогичными силами, действующими с другой стороны этого сечения. Следовательно, напряжение сдвига в этом сечении равно нулю, и материал движется подобно твердой пробке, не подвергаясь никаким деформациям сдвига. При дальнейшем движении материала это равновесие нарушается, и центральные слои начинают двигаться с большей скоростью, чем слои, прилегающие к поверхности валков. Максимальная разница достигается в минимальном сечении, расположенном на линии, соединяющей центры валков. Дальнейшее, движение сопровождаемся торможением центральных слоев. Наконец, на выходе из зазора избыточное давление падает до нуля, а профиль скоростей вновь принимает прямоугольную или трапециевидную форму.

— Из изложенного выше следует, что вальцевание представляет собой политропический процесс деформации среды, обладающей как аномалией вязкости, так и высокоэластичностью.

Поведение высокополимерных материалов при деформировании приближается к поведению неньютоновых (квазивязких жидкостей), поэтому процесс деформирования этих материалов в зеве валков можно рассматривать с позиций гидродинамики, как вязкое течение жидкости, увлекаемой в зазор вращающимися валками.

При выводе основных расчетных уравнений делается ряд допущений:

1. Режим течения материала в зазоре между валками из-за очень высокой вязкости полимера – ламинарный.

2. Материал прилипает к поверхностям валков, т. е. нет скольжения в относительном движении полимера и стенок, ограничивающих поток (слои материала, прилегающие к валкам, движутся с такой же скоростью, что и валки).

3. Гравитационные и инерционные силымалы по сравнению с силами поверхностными, и поэтому ими пренебрегают.

4. Течение материала рассматривается как одномерное, т. е. материал перемещается в основном в зазор (v_z=0; v_y«v_x и ¶v_x/¶y«¶v_y/¶y).

5. Гидромеханические давления на входе полимера в валки и выходе из них равны нулю. Давление в плоскостях, параллельных осям валков, не меняется направления оси y и z, т. е. ¶p/¶y=¶p/¶z=0.

— Во всех работах, посвященных гидродинамической теории вальцевания, в качестве исходных рассматриваются уравнения движения вязкой жидкости Навье-Стокcа, которые с учетом установившегося плоскопараллельного течения вязкой, жидкости в зазоре между валками и принятых выше условий имеют следующий приближенный вид:

,

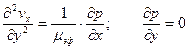(1)

где p – давление.

Уравнение (1) отличается от уравнений вязкой ньютоновской жидкости тем, что в это уравнение вместо коэффициента вязкости ньютоновской жидкости m входит коэффициент эффективной вязкости m_эф. Следует отметить, что при решении уравнения (1), как правило, исходят изтого, что эффективная вязкость материала в зазоре не изменяется существенным образом и связана с некоторым средним градиентом скорости. В этом случае m_эф для данного режима течения считают неизменным по всему сечению зазора, а уравнение (1) интегрируется так же, как и для случая течения ньютоновской жидкости. Затем на определенном этапе решения в полученные таким образом уравнения вместо величины m_эф подставляется ее значение при соответствующих значениях скорости сдвига. В этом случае расчетные уравнения выражаются через средний градиент скорости и константы течения. Возможен и более простой путь, когда в окончательные расчетные уравнения входит величина m_эф.

 

В зоне максимального давления ¶p/¶x=0, т.е. ¶v/¶y=const. В этой зоне скорость течения полимера равномерно изменяется от v₁ до v₂ (с учетом налипания материала на поверхность валков).

При интегрировании первого из уравнений (1) получаем

(2)

Подставляя вформулу (2) значение фрикции f=v₂/v₁ (отношение скоростей валков) и учитывая граничные условия (v|_–h/2=v₁; v|_h/2=v₂=fv₁),получим (определив постоянные С₁ и С₂) формулу

,

(3)

где h — текущая координата (расстояние между валками). Из геометрических соотношений следует, что

.

На основания уравнения (3) и определения величины потока в зазоре получено дифференциальное уравнение для давления (дифференцируется по h):

.

(4)

В этом уравнении знак (+) соответствует x>0, знак (–) соответствует x<0; h₁ соответствует зоне максимального давления, h_к – минимальный зазор между валками. При интегрировании уравнения (4) получены равные между собой константы интегрирования, анализ которых приводит к следующим соотношениям (приближенным):

hн=5hк	h1=1.20hк	С1=С2=0.41
hн=10hк	h1=1.21hк	С1=С2=0.48
hн=26hк	h1=1.22hк	С1=С2=0.51
hн=37hк	h1=1.22hк	С1=С2=0.51

Как видно, величина h₁ в зависимости от h изменяется незначительно, а при h_н>10h_к константы интегрирования приобретают постоянное значение.

При интегрировании исходного уравнения (1) при следующих граничных условиях: v_x=v₁ при y=–h/2; p=0 при y=±h_н/2; v_x=v₂=fv₁ при y=+h/2; p=0 при y=±h₂/2 получается зависимость для определения скоростей потока в различных сечениях зазора между валками (h_н – расстояние между валками на входе в зазор). Эта зависимость аналогична уравнению (3)

Производная ¶p/¶x определяется суммарным расходом

,

(5)

где L – длина бочки валка.

Если в уравнение (5) подставить значение v_x по уравнению (3) и проинтегрировать уравнение (5) в указанных пределах, то расход

.

(6)

В сечении максимального давления производная ¶p/¶x=0, поэтому расход через это сечение

.

(7)

В результате совместного решения уравнений (6) и (7), учитывая, что Q=Q₁,получим:

.

(8)

После подстановки выражения для dp/dx из уравнения (8) в уравнение (3) и замены h и h₁ безразмерными параметрами d=h/h_к и d₁=h₁/h_к получаем уравнение скорости

,

(9)

Эпюры скоростей указывают на неоднородность потока по полю скоростей. Существуют две принципиально различные области течения, которые разделены сечением x₂ (h_л). До сечения x₂ (h_л), которое можно считать началом развития ламинарного однонаправленного течения, наблюдается зона поступательного (смещена к поверхности валков) и зона встречного течения – противоток. Объем материала, который участвует в противотоке, постепенно уменьшается в направлении течения общего потока и совершенно исчезает в сечении x₂ (h_л).

Таким образом, между сечением входа h_н и сечением h_л вектор скорости частиц, расположенных у рабочей поверхности валков, совпадает с общим направлением течения, потока, В центральной области потока вектор скорости частиц имеет противоположное направление. За сечением h_л вектор скорости в направлении оси x изменяет знак на обратный. Между сечениями h_л и h₁ скорость частиц в центральной области вязкого течения материала возрастает от нуля до величины v_x=v₁(f+1)/2 в сечении h₁; эпюра скоростей приобретает вид трапеции, боковые стороны которой по абсолютной величине равны линейным скоростям валков. Для сечения максимального давления h₁ характерно, что в центре потоки, материал начинает опережать слои, прилегающие к поверхности валков, В центре сечения x₀ (h_к) скорость частиц деформируемой среды достигает максимального значения. Существование поступательного и встречного течения объясняет наблюдаемое на практике явление "вращения запаса". В сечении h₁ изменение скорости потока при наличии фрикции между валками подчиняется линейному закону с углом наклона прямой к оси y, тангенс которого tgj=v₁(1–f)/(dh_к).

Между сечениями h_л и h₂ вектор скорости любой частицы потока совпадает с общим направлением течения материала через зазор между валками.

Естественно, что при отношении окружных скоростей валков, равном единице, вершина параболы в различных сечениях зазора будет совпадать с осью х. При конечном значении фрикции f вершина параболы между сечениями h_н и h₁ смещается к поверхности валка с меньшей окружной скоростью, а между сечениями