Законы течения расплавов и растворов полимеров.

— Деформация идеально упругого тела описывается законом Гука (деформация пропорциональна приложенному напряжению). Деформация идеально вязкого тела описывается законом Ньютона (скорость деформации пропорциональна приложенному напряжению). Большинство тел не являются идеально упругими или идеально вязкими. Отсюда возникает необходимость описания деформации в реальном теле, в котором нельзя пренебречь изменением структуры при деформации.

— Уравнение Эйринга-Паулла.

,

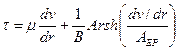где m, B, A_EP – эмпирические константы.

При низких скоростях сдвига получаем:

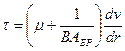
Это соотношение описывает ньютоновское течение, а выражение в скобках – ньютоновскую вязкость.

При промежуточных скоростях сдвига уравнение описывает неньютоновское поведение псевдопластичной жидкости.

При высоких скоростях сдвига можно пренебречь вторым слагаемым в правой части уравнения, и вновь получается уравнение ньютоновского течения.

Это уравнение имеет ряд недостатков: уравнение плохо описывает экспериментальные данные; теоретические предпосылки вывода недостаточно достоверны; данные трудно интерпретировать.

— Уравнение Оствальда-Вейла.

Здесь n – индекс течения, K – коэффициент консистентности, зависящий от температуры Т; K₀ – значение K при Т=Т₀; DЕ – энергия активации вязкого течения; R – универсальная газовая постоянная

Это уравнение часто применяется, хотя и не объясняет поведения в рассмотренных выше трех областях течения.

Макрокинетика.

2.3.1. Кинетические кривые и их классификация.

— Химические превращения в полимерах, как правило, сопровождаются побочными явлениями физико-химического характера: изменением агрегатного и/или физического состояния; смачиванием; образованием геля; тепловыми явлениями при возникновении деформаций и пр. Все это приводит к тому, что мы имеем возможность экспериментально оценить лишь обобщенные (брутто) характеристики процесса, не разделяя его на отдельные компоненты. Это обусловлено тем, что мы имеем дело с плохо организованными системами. Поэтому при изучении таких систем нас интересуют макрокинетические закономерности их физико-химических превращений.

— Кинетические кривые, характеризующие эти превращения, могут быть интегральными и дифференциальными.

— Интегральные кинетические кривые характеризуют степень завершенности рассматриваемого брутто-процесса. В качестве примеров таких кривых можно указать кривые, описывающие кинетику формирования сетки, кинетику изменения концентрации структурирующего агента, кинетику изменения величины энергии, затрачиваемой на создание сдвиговой деформации в процессе физико-химических превращений и др.

— Дифференциальные кинетические кривые характеризуют скорость превращения и могут быть получены дифференцированием интегральных кривых. Но существуют методы, которые позволяют непосредственно количественно характеризовать скорость. Сюда, прежде всего, следует отнести методы термического анализа.

— Интегральные кривые, как правило, носят S-образный характер. Точчке перегиба на интегральной кривой соответствует максимум на дифференциальной кривой. Однако максимум на дифференциальной кривой может не совпадать по времени с максимальным значением скорости.

— Рассмотрим это обстоятельство более подробно на примере анализа тепловыделений в плоской бесконечной пластине. Для этого найдем интенсивность внутренних источников из уравнения теплопроводности:

Из этого выражения видно, что интенсивность внутренних источников тепла вычисляется как алгебраическая сумма интенсивности аккумулированного теплового потока и теплового потока, отведенного теплопроводностью.

Разность температур в пластине DТ(х), обусловленная наличием внутренних истоников, представляется многочленом по степеням следующего вида: DТ=b₀x⁰+b₁x¹+b₂x²+…+b_nxⁿ. В силу граничных условий при х=0 (середина пластины) DТ=b₀; при x=R (толщина пластины) DТ=b₀R⁰+b₁R¹+b₂R²+…+b_nRⁿ Вычитая из первого многочлена второй, получим: T=T₀+b₁(x-R)+b₂(x²-R²)+…+b_n(xⁿ-Rⁿ). Тогда:

и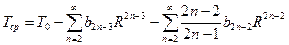

Подставляя эти два соотношения в выражение для интенсивности внутренних источников, получим:

При n=2 (если q_v¹f(x)), имеем:

Константы b₁ и b₂ можно найти, измеряя температуру в двух точках. Например, при x=0DТ_v= –b₁R–b₂R² и при x=R/2DТ_c= –b₁R/2–3b₂R²/4. Тогда b₁=(4DТ_c–3DТ_v)/R=b₁(t); b₂=(2DТ_v–4DТ_c)/R²=b₂(t).

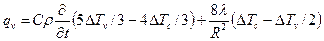
При b₁=0 (симметричная парабола), что эквивалентно равенству DТ_с–=3/4DТ_v, получим:

,

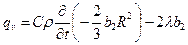где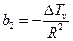

.

Окончательно получаем:

Для дальнейших расчетов необходимо получить приемлемую эмпирическую модель для DТ_v=f(t) и осуществить дифференцирование. Среди множества возможных моделей, выбор которых обсудим позднее, остановимся на следующей модели:

,

или ,

где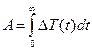

Здесь А, h и d – параметры модели, G(h) – гамма-функция, представляющая собой обобщение понятия факториала на дробные числа. Тогда, имея в виду, что DT_v'=DT_v((h-1)/t-d), получим следующее выражение для интенсивности внутренних источников:

,

,

где p зависит от принятой для DT_v модели, и в рассматриваемом случае имеет приведенный выше вид.

Таким образом, абсциссы максимумов на термограмме и на кинетической кривой интенсивности тепловыделений не совпадают, и тем больше, чем меньше критерий Фурье (Fo), т.е. коэффициент температуропроводности.

2.3.2. Интерпретация интегральных кривых.

— Количественная аппроксимация кинетических кривых необходима для создания баз данных, хранения и систематизации полученной информации.

— На рисунке показана интегральная кинетическая кривая процесса структурирования.

 

На этом же рисунке показаны 95 %-ные доверительные пределы (если повторять наблюдения бесчисленное множество раз 95 % попадут в обозначенный "коридор").

Модели интегральной кривой

№	Ранг	Номер	Модель
			b=a+b/(1+exp(-(t-c)/d))
			b=a+b0.5(1+erf((t-c)/(20.5d)))
			b=a+b/(1+(t/c)d)
			lnb=a+b/t0.5+ce-t
			lnb=a+blnt+ce-t
			lnb=a+b(lnt)2+ce-t
			lnb=a+bt0.5+ce-t
			lnb=a+bt+ce-t
			lnb=a+bxlnt+ce-t
			lnb=a+bt2+ce-t
			lnb=a+bet+ce-t
			lnb=a+b/t+ce-t
			lnb=a+be-t
			1-b=a+b/(1+exp(-(t-c)/d))
			1-b=a+b0.5(1+erf((t-c)/(20.5d)))
			1-b=a+b/(1+(t/c)d)

 

— По экспериментальным данным с использованием программы Table Curve были получены некоторые модели, которые сопоставляются между собой. Ранг модели соответствует ранжированию программы, а номер соответствует номеру каталога.

Критерии адекватности и параметры моделей

№	Критерии адекватности	Параметры моделей
	R2	S	F	a	b	c	d
	0.9996	0.01024		-0.0245	1.00978	3.30699	0.77405
	0.9994	0.01280		-0.0130	0.99457	3.32494	1.26955
	0.9993	0.01383		0.00938	0.99064	3.30303	-4.4315
	0.9990	0.01529		0.00679	-0.0620	-17.070
	0.9990	0.01531		-0.0641	0.02275	-16.828
	0.9990	0.01545		-0.0380	0.00483	-16.973
	0.9989	0.01546		-0.0561	0.01379	-16.973
	0.9989	0.01558		-0.0335	0.00203	-17.077
	0.9989	0.01564		-0.0270	0.00058	-17.129
	0.9989	0.01575		-0.0226	8.375e-5	-17.204
	0.9989	0.01604		-0.0154	3.253e-9	-17.379
	0.9989	0.01606		-0.0142	0.00103	-17.437
	0.9989	0.01505		-0.0142	-17.416
	0.9996	0.01024		0.01473	1.00979	3.30700	-0.7741
	0.9994	0.01280		0.01841	0.99457	3.32494	-1.2696
	0.9993	0.01383		-2.07e-5	0.99064	3.30303	4.43152

— Во второй таблице представлены следующие критерии адекватности модели.

Коэффициент детерминации (квадрат коэффициента корреляции между экспериментальными и рассчитанными значениями):

.

Стандартная ошибка:

.

Критерий Фишера:

.

В этих соотношениях индексы "э" и "р" означают "экспериментальный" и "рассчитанный", а черта наверху дается для среднего значения. N – число экспериментальных точек, p – количество коэффициентов в модели, b – степень завершенности процесса.

– функция ошибок.

— Параметры некоторых из этих моделей можно интерпретировать с физико-химической точки зрения

— В ряде случаев для нахождения параметров модели необходимо производить преобразование осей координат. Примером такого случая является уравнение Ерофеева-Колмогорова b=1–exp(–ktⁿ). Для нахождения параметров этого уравнения необходимо построить линеаризующую зависимость после двойного логарифмирования ln(ln(1/(1–b)))=lnk=n×lnt. Другой пример представляет собой аппроксимация кинетической кривой с помощью кривой роста Перла-Рида b=tⁿ/(a+tⁿ). Здесь для линеаризации достаточно однократного логарифмирования ln (b/(1–b))= –lna+n×lnt. Более удовлетворительные результаты дает представление кривой роста Гомперца b=exp(–b×exp(–kt)). Здесь прямая линия должна получиться в координатах: ln(–lnb)=lnb–kt.

— В случаях, когда различия между экспериментальными и рассчитанными значениями (невязки) слишком велики, можно рекомендовать разбить кривую на две (или больше) так, чтобы их суммированием (или вычитанием) получить желаемую зависимость. Другой способ получения более удовлетворительной модели может состоять в использовании дополнительных параметров. Можно, наконец, использовать описанные выше методы асимптотической коррекции.

2.3.3. Интерпретация дифференциальных кривых.

— На рисунке показана дифференциальная кинетическая кривая процесса структурирования и 95 %-ные доверительные пределы для нее.

 

— Количество приемлемых моделей в случае дифференциальных кинетических кривых больше, чем в случае интегральных кривых. Возможности физико-химического осмысления этих моделей к роются в использовании моделей, формально аналогичных функциям распределения случайных величин. Такой подход позволяет использовать чрезвычайно развитый математический аппарат, разработанный для их описания и интерпретации.

Модели дифференциальной кривой

№	Ранг	Номер	Модель
			lnb'=a+btlnt+ct0.5
			b'=a+bexp(-0.5((t-c)/d)2)
			lnb'=a+bt+ct0.5
			b'=a+b×4n/(1+n)2 n=exp(-(t-c)/d)
			lnb'=a+bt+ctlnt
			lnb'=a+btlnt+clnt
			lnb'=a+bt2+clnt
			lnb'=a+bt2+ce-t
			b'=a+bexp(-exp(-((t-c)/d))-((t-c)/d)+1)
			b'=a+berfc(((t-c)/d)2)
			lnb'=a+bt+clnt
			b'=a+bexp(-0.5(ln(t/c)/d)2)
			lnb'=a+btlnt+ce-t
			b'=a+b/(1+((t-c)/d)2)
			lnb'=a+bt+ce-t
			b'-1=a+bet+c/t
			lnb'=a+bt+ct2

— Мы можем видеть, что общий уровень адекватности модели в случае дифференциальных моделей ниже, чем в случае интегральных моделей. Правда объемы выборок несколько отличаются, что сказывается на результатах расчетов. В случае дифференциальных моделей выделено больше моделей с четырьмя параметрами, которые легко физико-химически интерпретируются.

Критерии адекватности и параметры моделей

№	Критерии адекватности	Параметры моделей
	R2	S	F	a	b	c	d
	0.9950	0.00778		-9.9793	-0.9068	6.81499
	0.9947	0.00832		0.00405	0.31960	3.24082	1.17388
	0.9946	0.00808		-12.812	-3.7974	13.3059
	0.9945	0.00852		0.00153	0.33053	3.23756	0.74602
	0.9944	0.00825		-6.9559	3.95391	-1.8442
	0.9922	0.00974		-3.3664	-0.5897	3.77660
	0.9909	0.01051		-2.8766	-0.1343	2.63918
	0.9902	0.01090		0.04324	-0.0804	-9.4766
	0.9900	0.01147		0.00169	0.32590	2.96522	1.10357
	0.9887	0.01220		0.00653	0.30353	3.24641	2.14488
	0.9882	0.01197		-1.6656	-1.8089	5.39850
	0.9868	0.01317		0.00415	0.32978	2.95646	0.35952
	0.9847	0.01362		0.36056	-0.2891	-11.046
	0.9826	0.01513		-0.0117	0.35838	3.25335	1.21888
	0.9788	0.01607		1.65118	-0.7186	-12.812
	0.9703	0.01900		-1.6239	0.04183	12.1670
	0.9643	0.02085		-3.6468	1.49872	-0.2305

— Среди полученных моделей встречаются и такие, которые могут рассматриваться как функции распределения случайных величин. Например, модель 1222 (№ 11) представляет собой гамма-распределение, модель 8005 (№ 12) представляет собой логарифмически нормальное распределение.

— Разработана система классификации кривых распределений. Все распределения объединены в систему Пирсона. В основу классификации положено дифференциальное уравнение, которое можно записать через вторую и первую производные ос степени превращения (b' – "ускорение" и b' –скорость процесса) и время t:

.

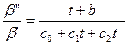Параметры этого уравнения b, с₀, с₁ и с₂ выражаются через статистические моменты распределений. Таких моментов четыре: математическое ожидание (среднее арифметическое), дисперсия (разброс относительно среднего), коэффициент асимметрии (в сравнении с симметричной кривой нормального распределения) и коэффициент эксцесса &крутовершинность кривой (в сравнении с кривой нормального распределения).

Кривые скорости с положительной асимметрией характеризуются малой величиной индукционного периода, экспериментальные точки группируются ближе к оси ординат. Такие кривые характерны для быстро протекающих процессов. С другой стороны, кривые с отрицательным значением коэффициента асимметрии соответствуют процессам с большим периодом индукции. Островершинные кинетические кривые характеризуюися положительными значениями коэффициента эксцесса. Кривые с пологими вершинами и многовершинные кривые имеют отрицательный коэффициент эксцесса.

— Для классификации кривых формируется критерий следующего вида:

;

.

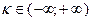— Существует семь типов кривых Пирсона:

I
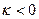
II
III
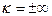
IV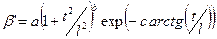
V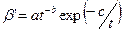
VI
VII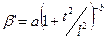

— Такая система дает возможность классифицировать дифференциальные кинетические кривые и на основе этого, имея своего рода паспорт композиции, организовать систему экспресс-контроля.

2.3.4. Кинетические модели.

— Рассмотрим в качестве примера кинетической модели уравнение кинетики необратимой реакции произвольного порядка:

.

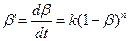Разделяя переменные и интегрируя, получим:

Следовательно, для определения параметров Аррениуса (константа скорости k и порядок реакции n) следует искать параметры модели следующего вида: ln(1–b)=a+blnt.

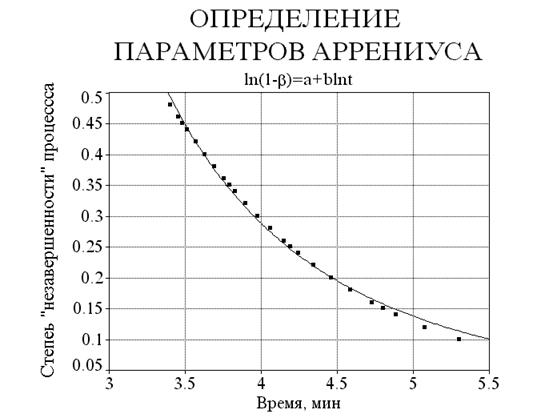Делать это рекомендуется в достаточно узкой области изменения величины bÎ[0.5; 0.9] или (1–b)Î[0.1; 0.5). Точки на рисунке взяты с кинетической кривой, а теоретическая кривая изображена сплошной линией. Модель имеет вид: ln(1–b)=3.3609–3.3228lnt. Отсюда n=1.30 и k=0.0203 c^-1.

— Если линеаризация данных в координатах lnt – ln(1–b) не дает удовлетворительного результата, можно прибегнуть к моделям, в которых учитывается зависимость константы скорости от степени завершенности процесса: b'=kb^m(1–b)ⁿ; b'=(k₁+k₂b^m)(1–b)ⁿ. И, наконец, в общем виде, учитывая зависимость обоих параметров Аррениуса от величины b: b'=k(b)(1–b)^n(b).

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: