Использование расчетных методов для ориентировочной оценки свойств полимеров.

— Принцип аддитивности представляет собой весьма эффективное средство в полуэмпирическом подходе к исследованию физических характеристик, вообще, и характеристик полимеров, в частности. Этот принцип означает, что большое количество характеристик, рассчитанных на моль вещества, можно вычислить путем суммирования вкладов атомов, групп или связей. Для практических целей следует отдать предпочтение методу групповых вкладов.

— Процедура формирования аддитивных величин определяется наличием корреляций между ними и какими-либо индивидуальными свойствами веществ. Например, линейная зависимость кубического корня из продольной скорости звука от плотности обусловливает возможность построения аддитивной молярной функции Рао U (эластохор):

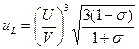
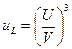
Здесь u_L – скорость продольной волны (м/с); U – функция Рао мономерного звена (м^10/3с^-1/3моль^-1); V – молярный объем мономерного звена (м³/с); s – коэффициент Пуассона; а – коэффициент температуропроводности (м²/с); l – длина свободного пробега фонона (принимается 6×10^-11 м).

Для полимеров в стеклообразном состоянии s составляет 0.33, для кристаллического состояния – 0.40 и, наконец, в случае каучуков – 0.49. тогда поправка составляет 0.994, и можно пользоваться третьей упрощенной формулой.

Таким образом, знание структуры мономерного звена позволяет прогнозировать величину функции Рао и далее скорость звука, теплопроводность и модуль упругости. Однако в ряде случаев при расчетах свойств по групповым вкладам (инкрементам) наблюдаются резкие различия между расчетными и экспериментальными величинами. Анализ причин таких различий представляет собой существенный источник информации для изучения структуры вещества и механизма протекающих в нем процессов.

Реология.

2.2.1. Предмет реологии.

— Реология – наука о течении и деформации реальных сплошных сред. Она рассматривает процессы, связанные с необратимыми остаточными деформациями вещества, и является областью науки, находящейся между гидродинамикой и теорией упругости. Обычные уравнения гидродинамики вязкой жидкости неприменимы для реологических тел, т.к. эти тела обладают аномалией вязкости. Если, например, для дисперсных систем применять закон течения Ньютона, вязкость их оказывается непостоянной, а меняется (уменьшается) с увеличением скорости течения.

2.2.2. Классификация жидкостей на основе их развившегося течения.

— Ньютоновская жидкость – это идеальная жидкость.

— В пространстве между двумя параллельными плоскостями площадью А каждая находится жидкость. Приложим к одной из плоскостей силу F. Будет происходить сдвиг, "сдвинутая" жидкость обратно не возвращается, соблюдается условие прилипания, то есть жидкость, соприкасающаяся с верхней поверхностью, движется с такой же скоростью v как и эта поверхность, а слои жидкости, соприкасающиеся с нижней поверхностью – неподвижны как и эта поверхность. Напряжение сдвига t связано с градиентом скорости dv/dr следующим соотношением (уравнение Ньютона):

,

где m – коэффициент динамической вязкости (Па×с), являющейся физической характеристикой материала.

— В идеальной жидкости деформация происходит во времени. За время dt верхняя плоскость перемещается на расстояние dL=vdt. Дифференциал деформации dg=dL/r=vdt/r. Следовательно, dg/dt=dv/dr, то есть

, g' – скорость сдвига (с^-1).

Представляет интерес сопоставление двух соотношений для идеальной жидкости и для идеального упругого твердого тела (G – модуль сдвига):

— Кривые течения представляют собой графические представления зависимости напряжения сдвига t от скорости сдвига (градиента скорости течения g'). Для ньютоновской жидкости вязкость m=const при данной температуре. Для неньютоновских жидкостей отношение t/g' не является постоянным при данной температуре, оно меняется с изменением касательного напряжения (или скорости сдвига g'). В этих случаях отношение напряжения сдвига к скорости сдвига называется эффективной вязкостью.

1 – Тело Бингама.

2 – Ньютоновская жидкость.

3 – Тело Сен-Венана.

4 – Дилатантная жидкость.

5 – Псевдопластичное тело.

— Кривые течения для различных жидкостей и зависимость вязкости от скорости сдвига качественно отражены на графиках.

— Тело Бингама – идеально пластичное, вязкопластичное тело. Отрезок, отсекаемый на оси ординат называется пределом текучести. Полимеры, течение которых начинается при любом напряжении сдвига, называются вязкими. Полимеры, обладающие предельным напряжением сдвига, ниже которого течение не возникает, называются пластичными. Бингамовская жидкость представляет собой упругое твердое тело ниже характеристического предела текучести и жидкость, когда напряжение сдвига больше этого предела t_у. При t_£t_уm=¥; при t>t_у m(g')=m₀+t_у/g'. Это эмпирическое уравнение описывает реологическое поведение латексов типа полимерных эмульсий, используемых в красках, паст и суспензий (кетчуп).

— Тело Сен-Венана может быть представлено элементом, лежащим на плоскости, и моделирует некоторые особые свойства жидкости. При этом элемент не обладает инерцией. Тело не начинает двигаться до тех пор, пока величина напряжения не превысит некоторого предельного значения. После этого может двигаться с любой скоростью. Модель тела Бингама состоит из последовательно соединенных вязкоупругого элемента и тела Сен-Венана.

— Дилатантные системы характерны для суспензий с большим содержанием твердых частиц. Они редко встречаются при переработке полимеров. При малых скоростях сдвига близки к ньютоновским жидкостям.

— Псевдопластичное тело. Ньютоновское поведение встречается редко, и обычно с ростом напряжения сдвига скорость течения растет быстрее, чем это следует из законы Ньютона. Ускорение течения обусловлено падением вязкости из-за изменения структуры полимера. Падение вязкости с ростом напряжения сдвига называется аномалией вязкости, а вязкость называется эффективной.

— Некоторые примеры. Рассмотрим кривые течения расплава полиэтилена при 125 ^оС (линия 1), раствора полиизобутилена при 25 ^оС (линия

2) и растворителя (линия 3). Последняя представляет собой прямую, характерную для ньютоновской жидкости (угол наклона 45^о). Кривая течения раствора располагается тем ниже, чем меньше его концентрация.

 

Поведение кривой течения раствора в начале и в конце кривой близко к ньютоновскому течению, а в середине – ближе к псевдопластичному телу. Этот переход к псевдопластичности не зависит от концентрации раствора. При больших значениях напряжения и скорости сдвига происходит ориентация и возникает течение ньютоновского характера.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: