 |
Скорость упругих волн в твердой среде
|
|
|
|
Для расчета скорости упругих волн необходимо получить волновое уравнение, описывающее распространение волн в твердой среде и, в соответствии с (22.26), приравнять квадратный корень из величины, обратной коэффициенту при производной по времени скорости распространения волны.
С этой целью рассмотрим продольную плоскую волну, распространяющуюся в вдоль оси Ох. Смещение из положения равновесия частиц 
зависит от координаты х: 
. Выделим в среде цилиндрический объем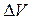 
с основанием 
и высотой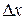 
, которую будем предполагать значительно меньшей длины рассматриваемой волны - рисунок 22.3. В некоторый момент времени смещение из положения равновесия основания с координатой х равно , а основания с координатой 
- 
. Поэтому при распространении волны объем 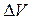деформируется, получая алгебраическое удлинение 
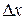. Среднее на длине относительное удлинение цилиндра равно 
. Истинное относительное удлинение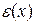 
в сечении с координатой х получим, устремив 
:
. (22.28)
Будем считать деформации в среде достаточно малыми, чтобы выполнялся закон Гука. Тогда механическое напряжение 
в среде связано с относительной деформацией соотношением:
, (22.29)
где 
- модуль Юнга среды.
Для того чтобы получить волновое уравнение, рассмотрим уравнение движения объема 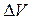. Положим высоту 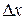достаточно малой, чтобы ускорение всех точек 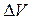можно было считать одинаковым и равным 
. Если плотность недеформированной среды равна 
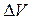, то масса цилиндра равна 
=
= 
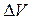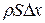. Ускорение деформированного цилиндра по второму закону Ньютона определяется результирующей силой 
, действующей на него, а она, в свою очередь, разностью деформаций цилиндра в сечениях с координатами х +x и х+Dx+x+Dx:
(22.30)
Поскольку 
величины малые, то по формуле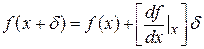 
для малых 
найдем:
|
|
|
и (22.31)
Подставим эти выражения в (22.30) и получим выражение для силы в виде:
. (22.32)
При малых (!) деформациях, когда только и справедлив закон Гука, 
, поэтому с высокой точностью в (22.32) можно пренебречь и считать:
. (22.33)
Теперь уравнение движения цилиндра 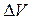по второму закону Ньютона можно записать в виде: 
откуда следует волновое уравнение для упругих волн в твердой среде:
. (22.34)
Сравнивая (22.34) и (22.26), видим, что скорость упругих волн в твердой среде
. (22.35)
Формула (22.35) получена нами для продольных волн. При распространении поперечных волн роль модуля Юнга играет модуль сдвига 
. Рассуждения, аналогичные проведенным выше, приводят к следующей формуле для скорости поперечных волн:
. (22.36)
При распространении звуковых волн в газах вследствие невысокой теплопроводности газов при значительной скорости протекающих процессов смежные участки среды не успевают обмениваться теплом, и процесс распространения волны является близким к адиабатическому. Скорость распространения волн в газе определяется давлением 
в невозмущенном волной газе, его плотностью и показателем адиабаты 
(отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме):
. (22.37)
Энергия упругой волны
Рассмотрим в среде, в которой распространяется упругая волна (22.10), 
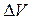элементарный объём достаточно малый, чтобы деформацию и скорость движения частиц в нём можно было считать постоянными и равными:
и 
. (22.37)
Вследствие распространения в среде волны объём 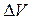обладает энергией упругой деформации
(22.38)
В соответствии с (22.35) модуль Юнга можно представить в виде 
. Поэтому:
. (22.39)
Рассматриваемый объём обладает также кинетической энергией:
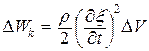. (22.40)
Полная энергия объёма:
. (22.41)
А плотность энергии:
. (22.42)
Но
, а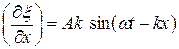 
(22.43)
Подставим эти выражения в (22.42) и учтем, что 
:
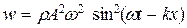. (22.44)
Таким образом, плотность энергии различна в разных точках пространства и меняется во времени по закону квадрата синуса.
|
|
|
Среднее значение квадрата синуса равно 1/2, а значит среднее по времени значение плотности энергии в каждой точке среды, в которой распространяется волна:
. (22.45)
Выражение (22.45) справедливо для всех видов волн.
Итак, среда, в которой распространяется волна, обладает дополнительным запасом энергии. Следовательно, волна переносит с собой энергию.
|
|
|
