Первые модели нейронной сети

Санкт-Петербургский Государственный морской

Технический университет

факультет морского приборостроения

кафедра САУ и БВТ

 

 

КОНСПЕКТ ЛЕКЦИЙ

По предмету: «Искусственные нейронные сети»

 

 

 

Санкт-Петербург

Оглавление

Тема 1 Введение. 3

Тема 2. Модели ИНС.. 8

2.1 Первые модели нейронной сети. 8

2.2 Прикладные возможности нейронных сетей. 10

2.3 Моделирование нейронных структур мозга. Модель нейрона. 12

2.3.1 Моделирование нейронов мозга. 12

2.3.2 Примеры искусственных нейронных сетей. 15

2.3.3 Различные типы нейронов. 16

2.3.4. Задачи нейронных сетей. Основные свойства. 17

Тема 3 Методы обучения Н.С. 19

3.1 Обучение нейронных сетей. 19

3.2 Процедуры адаптации и обучения. 20

3.3 Способы адаптации и обучения. 26

3.4 Методы обучения. 38

3.4.1 Обучение однослойной сети. 38

3.4.2 Обучение многослойной сети. 40

3.5 Алгоритмы обучения. 45

Список литературы.. 46

Тема 1 Введение

 

За последние годы компьютерная техника достигла таких вычислительных мощностей, которые позволяют решать с ее помощью широкий круг задач в различных областях научного и инженерно-прикладного характера. Основой развития компьютеров фон-неймановского типа является увеличение тактовой частоты центрального процессора, увеличение его разрядности и соответственно объема адресуемой оперативной памяти.

Однако существует ряд так называемых интеллектуальных задач, которые характеризуются НЕ-факторами (неточность, неопределенность, недостоверность, неполнота информации и т.п.) и часто необходимостью в обработке в реальном времени больших массивов различным образом формализованной и структурированной информации. К таким задачам относятся, например:

§ автоматическое построение текстов;

§ машинный перевод текстов;

§ обработка визуальной информации.

Реализация алгоритма решения этих задач на обычных компьютерах фон-неймановского типа весьма затруднительна и нецелесообразна, а часто – и невозможна. Необходимость в решении подобных задач явилась одной из предпосылок к созданию компьютеров не-фон-неймановского типа. Одним из направлений в этой области являются нейрокомпьютеры. В основе работы нейрокомпьютеров лежит использование формальных моделей функционирования биологических нейронных сетей. Отличия таких компьютеров от компьютеров фон-неймановского типа:

§ многопроцессорность;

§ ассоциативная память;

§ параллельно распределенная организация вычислений;

§ отсутствие необходимости программирования;

§ высокая «живучесть».

Из этих особенностей следует:

§ применяется стандартный способ решения любых задач;

§ вместо программирования производится обучение, то есть аккумулирование априорных знаний;

§ высокий внутренний параллелизм алгоритмического и аппаратного обеспечения;

§ гибкость структуры.

Тематика искусственных нейронных сетей относится к междисциплинарной сфере знаний, связанных с биокибернетикой, электроникой, прикладной матема­тикой, статистикой, автоматикой и даже с медициной. Искусственные нейронные сети возникли на основе знаний о функционировании нервной системы живых существ. Они представляют собой попытку использова­ния процессов, происходящих в нервных системах, для выработки новых техно­логических решений.

Нервная клетка, сокращенно называемая нейроном, является основным эле­ментом нервной системы. Изучение механизмов функционирования отдельных нейронов и их взаимодействия принципиально важно для познания протекающих в нервной системе процессов поиска, передачи и обработки информации. С этой точки зрения представляется необходимым построить и изучить модель биологического нейрона.

Как и у любой другой клетки, у нейрона имеется тело со стандартным набором органелл, называемое сомой, внутри которого располагается ядро. Из сомы нейрона выходят многочисленные отростки, играющие ключевую роль в его взаимодействии с другими нервными клетками. Можно выделить два типа отростков: многочисленные тонкие, густо ветвящиеся дендриты и более толстый, расщепляющийся на конце аксон (рис. 1).

Входные сигналы поступают в клетку через синапсы, тогда как выходной сигнал отводится аксоном через его многочисленные нервные окончания, назы­ваемые колатералами. Колатералы контактируют с сомой и дендритами других нейронов, образуя очередные синапсы. Очевидно, что синапсы, подключающие к клетке выходы других нейронов, могут находиться как на дендритах, так и непосредственно на теле клетки.

Передача сигналов внутри нервной системы - это очень сложный электрохи­мический процесс. С большим упрощением можно считать, что передача нерв­ного импульса между двумя клетками основана на выделении особых химических субстанций, называемых нейромедиаторами, которые формируются под влиянием поступающих от синапсов раздражителей. Эти субстанции воздействуют на клеточную мембрану, вызывая изменение ее энергетического потенциала, причем величина этого изменения пропорциональна количеству нейромедиатора, попадающего на мембрану.

 

Рис. 1. Упрощенная структура биологической нервной клетки

 

Синапсы отличаются друг от друга размерами и возможностями концен­трации нейромедиатора вблизи своей оболочки. По этой причине импульсы одинаковой величины, поступающие на входы нервной клетки через различные синапсы, могут возбуждать ее в разной степени. Мерой возбуждения клетки считается уровень поляризации ее мембраны, зависящий от суммарного количества нейромедиатора, выделенного на всех синапсах.

Из сказанного следует, что каждому входу клетки можно сопоставить численные коэффициенты (веса), пропорциональные количеству нейромедиатора, однократно выделяемого на соответствующем синапсе. В математической модели нейрона входные сигналы должны умножаться на эти коэффициенты для того, чтобы корректно учитывать влияние каждого сигнала на состояние нервной клетки. Синапсические веса должны быть натуральными числами, принимаю­щими как положительные, так и отрицательные значения. В первом случае синапс оказывает возбуждающее, а во втором - тормозящее действие, препятствующее возбуждению клетки другими сигналами. Таким образом, действие возбуждаю­щего синапса может моделироваться положительным значением синапсического веса, а действие тормозящего синапса - отрицательным значением.

В результате поступления входных импульсов на конкретные синапсы и высвобождения соответствующих количеств нейромедиатора происходит опреде­ленное электрическое возбуждение нервной клетки. Если отклонение от состояния электрического равновесия невелико либо если баланс возбуждений и торможений является отрицательным, клетка самостоятельно возвращается в исходное состояние, и на ее выходе какие-либо изменения не регистрируются. В этом случае считается, что уровень возбуждения клетки был ниже порога ее срабатывания. Если же сумма возбуждений и торможений превысила порог активации клетки, значение выходного сигнала начинает лавинообразно нарастать, принимая характерный вид нервного импульса (рис. 1.2), пересылае­мого аксоном на другие нейроны, подключенные к данной клетке. Величина этого сигнала не зависит от степени превышения порога. Клетка действует по принципу "все или ничего". После выполнения своей функции нейромедиатор удаляется. Механизм удаления заключается либо во всасывании этой субстанции клеткой, либо в ее разложении, либо в удалении за пределы синапса.

 

 

Рис. 2. Типичная форма нервного импульса

 

Одновременно с генерацией нервного импульса в клетке запускается процесс рефракции. Он проявляется как стремительное возрастание порога активации клетки до значения "плюс бесконечность", в результате чего сразу после генерации импульса нейрон теряет способность вырабатывать очередной сигнал даже при сильном возбуждении. Такое состояние сохраняется в течение времени At_r, называемого периодом абсолютной рефракции. По окончании этого срока наступает период относительной рефракции At_w, за который порог срабатывания возвращается к первоначальному значению. В это время клетку можно активировать, но только с приложением более сильных возбуждений. В естественных процессах, как правило, выполняется отношение At_w» At_r.

Количество взаимодействующих друг с другом нервных клеток чрезвычайно велико. Считается, что человеческий мозг содержит около 10¹¹ нейронов, каждый из которых выполняет относительно примитивные функции суммирова­ния весовых коэффициентов входных сигналов и сравнения полученной суммы с пороговым значением. Каждый нейрон имеет свои веса и свое пороговое значе­ние. Они определяются местонахождением нейрона и решаемой им задачей и могут интерпретироваться аналогично содержимому локальной памяти процессора.

Громадное количество нейронов и межнейронных связей (до 1000 входов в каждый нейрон) приводит к тому, что ошибка в срабатывании отдельного нейрона остается незаметной в общей массе взаимодействующих клеток. Нейронная сеть проявляет высокую устойчивость к помехам - это "стабильная" сеть, в которой отдельные сбои не оказывают существенного влияния на результаты ее функционирования. Таково главное отличие нейронных систем от обычных электронных систем, созданных человеком. Следует подчеркнуть, что ни одна современная технология не позволяет построить искусственную нейронную сеть, близкую по масштабам к нейронной сети мозга. Однако изучение и копирование биологических нервных систем позволяют надеяться на создание нового поколения электронных устройств, имеющих аналогичные характеристики.

Другая важная особенность нервных систем - высокая скорость их функционирования, несмотря на относительно длительный цикл срабатывания каждой отдельной клетки, измеряемый в миллисекундах. Она достигается благодаря параллельной обработке информации в мозге огромным количеством нейронов, соединенных многочисленными межней­ронными связями. Такие операции, как распознавание образов и звуков либо принятие решений, выполняются человеческим мозгом за промежутки времени, измеряемые миллисекундами. Достижение такого результата при использовании полупроводниковой технологии VLSI все еще выходит за границы современных технических возможностей, хотя цикл срабатывания отдельных исполнительных элементов СБИС является достаточно коротким и имеет порядок 10^-8 с. Если удастся, взяв за образец нервную систему, создать устройство с высокой степенью параллельности выполнения независимых операций, то скорость его функцио­нирования может быть существенно увеличена и приближена к уровню, наблюдаемому в процессах обработки информации биологическими объектами.

 

Тема 2. Модели ИНС

Первые модели нейронной сети

 

Из приведенных выше рассуждений следует, что каждый нейрон можно считать своеобразным процессором: он суммирует с соответствующими весами сигналы, приходящие от других нейронов, выполняет нелинейную (например, пороговую) решающую функцию и передает результирующее значение связанным с ним нейронам. В соответствии с действующим правилом "все или ничего" в простейших моделях нейронов выходной сигнал принимает двоичные значения: 0 или 1. Значение 1 соответствует превышению порога возбуждения нейрона, а значение 0 - возбуждению ниже порогового уровня.

В одной из первых моделей нейрона, называемой моделью МакКаллока-Питса (предложенной в 1943 г.), нейрон считается бинарным элементом. Структурная схема этой модели представлена на рис. 3. Входные сигналы x_j, (j = 1, 2,..., N) суммируются с учетом соответствующих весов wy (сигнал поступает в направлении от узла i к узлу j)в сумматоре, после чего результат сравнивается с пороговым значением w_j0. Выходной сигнал нейрона у_i определяется при этом зависимостью

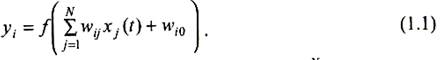
Аргументом функции выступает суммарный сигнал 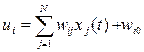. Функция f (u_i) называется функцией активации. В модели МакКаллока-Питса это пороговая функция вида

 

 

Коэффициенты w_ij, присутствующие в формуле (1.1), представляют веса синаптических связей. Положительное значение w_ij соответствует возбуждающим синапсам, отрицательное значение w_ij -тормозящим синапсам, тогда как w_ij = 0 свидетельствует об отсутствии связи Между i -м и j -м нейронами. Модель МакКаллока-Питса - это дискретная модель, в которой состояние нейрона в момент (t + 1) рассчитывается по значе­ниям его входных сигналов в предыду­щий момент t. Построение дискретной модели обосновывается проявлением рефракции у биологических нейронов, нервной клетки по приводящей к тому, что нейрон может наменять свое состояние с конечной чистотой, причем длительность периодов бездействия зависит от частоты его срабатывания.

 

 

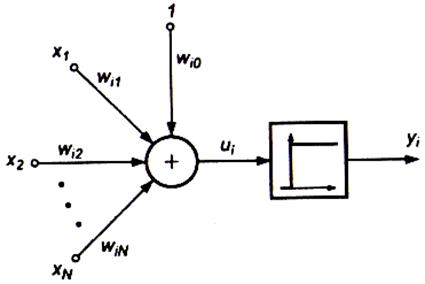
Рис. 3. Модель нервной клетки по МакКаллоку—Питсу

 

Через несколько лет Д. Хебб в процессе исследования ассоциативной памяти предложил теорию обучения (подбора весов w_ij) нейронов. При этом он использовал наблюдение, что веса межнейронных соединений при активации нейронов могут возрастать. В модели Хебба приращение веса Δ w_ij в процессе обучения пропорционально произведению выходных сигналов у_i и y_j нейронов, связанных весом w_ij:

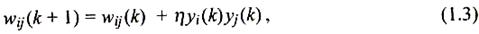
где k означает номер цикла, а 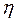- это коэффициент обучения.

В начале 60-х годов Б. Видроу предложил теоретическое обоснование и сформулировал принципы практической реализации адаптивных устройств обработки сигналов, что стало существенным вкладом в развитие нейронных сетей, функционирующих в режимах "онлайн" и "оффлайн".

В 1962 г. была опубликована книга Ф. Розенблатта, в которой представлена теория динамических нейронных систем для моделирования мозговой деятельности, основанная на персептронной модели нервной клетки. В этой теории использовалось представление нейрона моделью МакКаллока-Питса, в которой функция активации принимала двоичные значения 0 и 1.

Ограниченные возможности одиночного персептрона и составляемых из таких элементов одноуровневых сетей подверглись критике в книге М. Минского и С. Пейперта, что вызвало резкое снижение финансирования этой сферы научных исследований и привело в результате к замедлению развития искусственных нейронных сетей. Только отдельные научные группы, сконцентрированные вокруг таких ученых, как Гроссберг, Видроу, фон дер Мальсбург, Амари, Фукушима и Кохонен, продолжали работу в этой области. И только бурное развитие в 80-х годах технологии производства полупровод­никовых устройств сверхвысокой степени интеграции (VLSI) привело к резкому возрастанию интереса к средствам параллельной обработки информации, которыми считаются и искусственные нейронные сети. Начиная с опубли­кованных в 1982 г. работ Дж. Хопфилда, теория нейронных сетей развивается и стремительном темпе, а количество научных центров, занимающихся этой междисциплинарной сферой знаний, непрерывно увеличивается. Доработка или, точнее, повторное открытие принципа обратного распространения в применении к обучению многослойных сетей сняли те ограничения, которые стали главным объектом критики в книге М. Минского и С. Пейперта. Масштабное увеличение финансирования этой научной отрасли предопределило существенный прогресс как в теории, так и в практических приложениях. С учетом взрывного развития вычислительных систем это создало базу для реализации новых технологических решений в сфере технического распоз­навания образов, восприятия и объяснения, в управлении сложными системами, для обработки речевых сообщений и т.п. В настоящее время искусственные нейронные сети представляют собой высокоразвитую (особенно в теоретическом аспекте) отрасль знаний.

 

 

2.2 Прикладные возможности нейронных сетей

 

Любая нейронная сеть используется в качестве самостоятельной системы представления знаний, которая в практических приложениях выступает, как приняло, в качестве одного из компонентов системы управления либо модуля принятия решений, передающих результирующий сигнал на другие элементы, не связанные непосредственно с искусственной нейронной сетью. Выполняемые сетью функции можно распределить на несколько основных групп: аппроксимации и интерполяции; распознавания и классификации образов; сжатия данных; прогнозирования; идентификации; управления; ассоциации.

В каждом из названных приложений нейронная сеть играет роль универсального аппроксиматора функции от нескольких переменных, реализуя нелинейную функцию

где x - это входной вектор, а у - реализация векторной функции нескольких переменных. Постановки значительного количества задач моделирования, идентификации и обработки сигналов могут быть сведены именно к апроксимационному представлению.

Для классификации и распознавания образов сеть обучается важнейшим их признакам, таким, как геометрическое отображение точечной структуры изображения, относительное расположение важнейших элементов образа, компоненты преобразования Фурье и другие подобные факторы. В процессе обучения выделяются признаки, отличающие образы друг от друга, которые и составляют базу для принятия решений об отнесении образов к соответствующим классам.

При решении задач прогнозирования роль нейронной сети состоит в предсказании будущей реакции системы по ее предшествующему поведению. Обладая информацией о значениях переменной х в моменты, предшествующие прогнозированию х(k-1), х(k-2),..., x(k-N), сеть вырабатывает решение, каким будет наиболее вероятное значение последовательности х(k) в текущий момент k. Для адаптации весовых коэффициентов сети используются фактическая погрешность прогнозирования £=х(k)-х(k) и значения этой погрешности в предшествующие моменты времени.

При решении задач идентификации и управления динамическими процессами нейросеть, как правило, выполняет несколько функций. Она представляет собой нелинейную модель этого процесса, обеспечивающую выработку соответст­вующего управляющего воздействия. Сеть также выступает в роли следящей системы, адаптирующейся к изменяющимся условиям окружающей среды. Очень большое значение, особенно при управлении роботами, имеет функция классификации, реализуемая при выработке решения о дальнейшем развитии процесса.

В задачах ассоциации нейронная сеть играет роль ассоциативного запоминающего устройства (ЗУ). Можно выделить ЗУ автоассоциативного типа, с помощью которых определяется корреляция между отдельными компонентами одного и того же входного вектора, и ЗУ гетероассоциативного типа, средствами которых устанавливается корреляция между двумя различными векторами. Если па вход сети подается неструктурированный вектор (например, содержащий искаженные шумом компоненты или вообще не содержащий отдельные компоненты), нейронная сеть сможет восстановить оригинальный и очищенный от шумов вектор и сгенерировать при этом полную версию ассоциированного с ним вектора.

Важнейшее свойство нейронных сетей, свидетельствующее об их огромном потенциале и широких прикладных возможностях, состоит в параллельной обработке информации одновременно всеми нейронами. Благодаря этой способности при большом количестве межнейронных связей достигается значительное ускорение процесса обработки информации. Во многих ситуациях становится возможной обработка сигналов в реальном масштабе времени.

Очень большое количество межнейронных соединений приводит к тому, что сеть становится нечувствительной к ошибкам, возникающим в отдельных контактах. Функции поврежденных соединений принимают на себя другие элементы, в результате в деятельности сети не наблюдаются заметные нарушения. Это свойство используется, в частности, при поиске оптимальной архитектуры нейронной сети путем разрыва отдельных связей. Алгоритм такого поиска, названный “Optimal Brain Damage”, является прекрасной иллюстрацией этого свойства нейронной сети.

Другое не менее важное свойство нейронной сети состоит в способности к обучению и к обобщению полученных знаний. Сеть обладает чертами так называемого искусственного интеллекта. Натренированная на ограниченном множестве обучающих выборок, она обобщает накопленную информацию и вырабатывает ожидаемую реакцию применительно к данным, не обрабатывав­шимся в процессе обучения. Несмотря на значительное количество уже известных практических приложений искусственных нейронных сетей, возможности их дальнейшего использования для обработки сигналов не изучены окончательно, и можно высказать предположение, что нейронные сети еще в течение многих лет будут средством развития информационной техники.

 

 

1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: