Моделирование нейронных структур мозга. Модель нейрона

 

Моделирование нейронов мозга

 

Искусственные нейронные сети (НС) представляют собой простейшие математические модели мозга. Понять основные принципы построения НС можно, рассматривая их как сово­купность (сеть) отдельных структур (нейронов). Очень грубо структуру биологического нейрона можно описать следую­щим образом. Нейрон имеет сому — тело, дерево входов — дендриты, выход — аксон. На соме и на дендритах распола­гаются окончания аксонов других нейронов, называемых си­напсами. Принятые синапсами входные сигналы стремятся либо возбудить нейрон, либо затормозить. Когда суммарное возбуждение достигает некоторого порога, нейрон возбуждается и посылает по аксону сигнал другим нейронам. Каждый синапс обладает уникальной синоптической силой, которая пропорционально своему значению изменяет передаваемый на нейрон входной сигнал. В соответствии с данным описанием математическая модель нейрона представляет собой суммирующий пороговый элемент.

Входные сигналы искусственного нейрона умножаются ни веса связей, суммируются и сравниваются с порогом. Пороговые суммирующие элементы объединяются в сеть. Соединение можно выполнить произвольным образом, но в таком случае переключение нейронов становится необозримым, по этому используют упрощенные структуры, например слоистые сети прямого распространения сигнала или специальные сети с обратными связями. На рис. 4.1 представлена трехслойная сеть прямого распространения. Внутренний слой нейронов называют скрытым. Каждая связь обладает определенным весом Wij.

Представим один узел нейронной сети (рис. 4.2). Любой нейрон характеризуется следующими параметрами:

1. Вектор входов Х= (Xj..., Х_п).

2. Вектор выходов О = {О₁..., О_т).

3. Вектор весов W= (W₁.'.., W_n).

4. Порог срабатывания 0.

5. Функция активации F(табл. 4.1).

Рис. 4. Многослойная НС прямого распространения сигнала

 

Рис. 5. Искусственный нейрон

 

 

Формула срабатывания нейрона:

На рис. 4.2 приложения приведены графики распростра­ненных функций активации — сигмоид. Для большинства ре­альных задач, решаемых нейросетями, используются нейро­ны с униполярной сигмоидальной функцией активации.

Наиболее часто используемые функции активации

Таблица 4.1

Название функции	Формула
Линейная Функция «знак» Униполярная сигмоидальная Биполярная сигмоида Гиперболический тангенс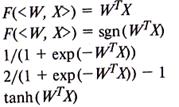

 

Примеры искусственных нейронных сетей

Пусть имеется нейрон с двумя входами и одним выходом, причем и входы, и выход - бинарные: X₁, X₂, O є [0, 1]. Какими должны быть веса (W\, W2), и значение порога (0), чтобы нейрон реализовывал функцию логического И и логического ИЛИ (рис. 4.3.)?

Если моделировать функцию И, то выход

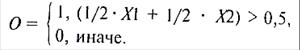
Следовательно, вектор весов(W₁, W2) = (1/2_; 1/2), порог

Ǿ = 0,5 превращаютискусственный нейрон в элемент логическое И.

 

х1	х2	или	и

 

 

 

Рис. 6. Функции логическое И и ИЛИ

 

Если моделируем функцию ИЛИ, то выход

Следовательно, для реализации функции ИЛИ необходимо установить вектор весов (W₁, W₂) = (1,1), порог Ǿ = 0,5.

 

 

Различные типы нейронов

 

Допустим, имеется нейрон, представленный на рис. 4.4, а. Порог срабатывания можно установить на 0, если ввести фиктивный вход, равный 1, с весом связи Ǿ (рис. 4.4, б).

Кроме традиционного линейного суммирующего порогового нейрона для построения специализированных видов сетей ис­пользуются различные виды нейронов, одним из которых явля­ется радиальный базисный нейрон (РБН, Radial PostSynapce unit). Радиальные синаптические элементы вычисляют квадрат расстояния между двумя точками в N-размерном про­странстве (где N – количество входов). Радиальные базисные нейроны имеют эквивалентные значения выходов, лежащие на гиперсферах в пространстве образцов. С помощью радиаль­ных базисных нейронов строят классификаторы, которые из­меряют расстояния между точками в пространстве признаков.

 

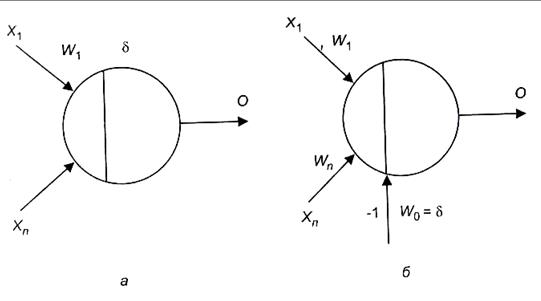
Рис. 7 Нейроны — без фиксированного входа (а);с фиксированным

входом (б)

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: