Задачи нейронных сетей. Основные свойства

Нейронные сети являются ровесниками компьютеров фон-неймановской архитектуры. В настоящее время усиливается значение параллельных распределенных вычислительной архитектур. На основе нейронных сетей можно построите параллельный нейрокомпьютер, основным операционными устройством которого будет нейронная сеть, а не арифметико-логический процессор. Нейронные сети как вычислительные элементы обладают универсальностью и очень важными интеллектуальным свойством – обучаемостью. Их значение в информатике выросло настолько, что говорят о нейронном буме. Нейронные сети, рассматриваемые как вычислители для адаптации к конкретной задаче, не нуждаются в програм­мировании, а настраиваются за счет изменения матриц синаптических весов. Обучение рассматривается как специаль­но организованный процесс предъявления образцов, каждый из которых имеет структуру, состоящую из стимула (входа) и реакции (выхода). Совокупность образцов называется обучающей выборкой. Если задана обучающая выборка, т. е. несколько строк, со следующей структурой:

< Входы 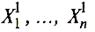— выходы >,

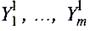то можно ввести обозначение К:

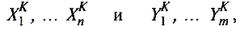
где К – номер образца в обучающей выборке.

Последовательно используя строки обучающей выборки, необходимо вычислить реакцию нейронной сети, т. е. ее вы­ход при текущих значениях матрицы весов. Для того чтобы приблизить выход сети к желаемому значению, можно изме­нять вектор весов. Уточним содержание задачи обучения ней­ронной сети.

Необходимо найти вектор весов, который давал бы нам заданный выход:

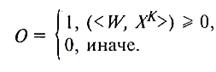
С математической точки зрения процесс обучения ней­ронной сети, которая может выполнять только операции ум­ножения, сложения и композиции функций за счет каскадирования, рассматривают как поиск аппроксимации с по­мощью суперпозиции непрерывных функций.

Настройка НС может рассматриваться и как поиск реше­ния задачи классификации объектов, описанных входными признаками, т. е. если (<W^T, X>) ≥ 0, то объект относится к классу С₁; если (<W^T, Х>) < О, то – к классу С₂. Тогда получаем НС – классификатор, который распознает класс объектов С₁, когда на выходе 1, и класс С₂, когда на выходе 0.

Проблема классификации – это задача отнесения предъяв­ленного объекта к одному из известных классов из опреде­ленного множества. На практике классификация объектов очень важна для распознавания образов, например для рас­познавания рукописного текста, речи или изображений. Обу­чение часто сводится к формированию способности распознавать объекты проблемной области или классифицировать их Важнейшая черта любой интеллектуальной системы (ис­кусственной или естественной) – это способность формиро­вать понятия. Оставим в стороне философские, лингвистиче­ские, семантические и другие аспекты сложнейшей проблемы и рассмотрим формирование понятий как математическую задачу кластеризации.

Допустим, имеется множество образцов-описаний объектов в пространстве признаков, но нам ничего не известно об их принадлежности каким-либо классам и количество последних. Способна ли нейронная сеть сыграть роль интеллек­туального устройства, на вход которого поступили все описа­ния объектов, а устройство научилось разбивать образцы на классы, определило понятия проблемной области, количество классов, их характерные черты? Характеристическую ин­формацию о классах можно считать понятиями проблемной области. Формирование системы классов является задачей кластеризации и успешно решается НС особого вида – ассо­циативными картами Т. Кохонена.

В связи с тем что нейронные сети решают задачу аппроксимации, они способны предсказать реакцию на никогда не предъявляемый им стимул, т. е. осуществить прогнозирова­ние НС широко используют для прогнозирования поведения различных финансовых и экономических индексов.

"терминологическую политику". При переводе монографии С. Осовского мы старались соблюдать принцип стилистического единства текста (особенно в плане использования профессиональных англицизмов), а также максимально корректно применять правила англо-русской транскрипции и транслитерации.

В необходимых случаях наряду с используемыми в книге переводными терминами приводятся их наиболее распространенные русифицированы аналоги.

Издание рассчитано на читателя, обладающего определенной математической подготовкой. Предполагается, что он знаком с основными понятиями линейной алгебры, дифференциального исчисления, теории оптимизации, теории вероятности и теории множеств.

Хочется верить, что публикация книги С. Осовского на русском языки станет еще одним стимулом для повышения эффективности как проводимым так и планируемых в России исследований в области нейронных сетей.