Главная | Обратная связь | Поможем написать вашу работу!

Xlabel(''), ylabel('Выходы a(i)'),grid

⇐ ПредыдущаяСтр 6 из 7Следующая ⇒

Subplot(3,1,2)

plot(0:63,[[0 0]; W],'k') % Рис.3.2,б

xlabelf¹¹), ylabeK'Beca входов w(i)'),grid

subplot(3,1,3) semilogy(l:63, ее,'+k') % Рис.3.2,в

Xlabel('Циклы'), ylabel('Ошибка'),grid

Рис. 9

Как следует из анализа графиков, для достижения требуемой точности адаптации требуется 12 шагов. Сравнивая рис. 9 и 8, можно убедиться, что существует различие в динамике процедур адаптации при последовательном и групповом представлении данных.

Динамические сети. Эти сети характеризуются наличием линий задержки, и для них последовательное представление входов является наиболее естественным.

Последовательный способ. Обратимся к линейной модели нейронной сети с одним входом и одним элементом запаздывания. Установим начальные условия на линии задержка

а также для весов и смещения равными 0, а параметр скорости настройки равным 0.5:

net = newlin([-l 1],1,[0 1],0.5);

Pi = {0}; % Начальное условие для элемента запаздывания

net.IW{l} = [0 0]; % Значения весов

net.biasConnect = 0; % Значение смещения

Чтобы применить последовательный способ адаптации, представим входы и цели как массивы ячеек:

Р = {-1/2 1/3 1/5 1/4}; % Вектор входа

Т = { -1 1/6 11/15 7/10}; % Вектор цели

Попытаемся приспособить сеть для формирования нужного выхода на основе сле дующего соотношения:

y(t) = 2p(t)+p(t-l).

Используем для этой цели М-функцию adapt и основной цикл адаптации сети с задан ной погрешностью, как это уже было описано выше:

ЕЕ = 10; i = 1;

while ЕЕ > 0.0001

[net,a{i},e{i},pf] = adapt(net,P,T);

W(i,:)=net.IW{l,l};

ЕЕ = mse(e{i});

ee(i) = ЕЕ;

i = i+1;

End

Сеть адаптировалась за 22 цикла. Результатом адаптации при заданной погрешности являются следующие значения коэффициентов линейной зависимости, значений выходов нейронной сети, приближающихся к значениям желаемого выхода, а также среднеквадратичная погрешность адаптации:

W(22,:)

ans = 1.983 0.98219

а{22}

ans = [-0.98955] [0.17136] [0.72272] [0.69177]

ЕЕ

ЕЕ = 7.7874е-005

Построим графики зависимости выходов системы и весовых коэффициентов от числа циклов обучения (рис. 3.3):

Subplot(3,1,1)

plot(0:22,[zeros(l,4); cell2mat(cell2mat(a¹))],'fc') % Рис.3.3,a

Xlabel('’), ylabelCВыходы a(i)’),grid

Subplot(3,1,2)

plot(0:22,[[0 0]; W],'k") % Рис.3.3,б

Xlabel('')(ylabel('Beca входов w(i)'),grid

Subplot(3,l,3)

semilogy(l:22,ee,'+k') % Рис.3.3,в

xlabel('Циклы¹), ylabel('Ошибка'),grid

Рис. 10

На рис. 10 а показаны выходы нейронов в процессе адаптации сети, а на рис. 10 б – коэффициенты восстанавливаемой зависимости, которые соответствуют элементам:-тора весов входа.

Групповой способ представления обучающего множества для адаптации динамичестем систем не применяется.

Обучение нейронных сетей

Статические сети. Воспользуемся рассмотренной выше моделью однослойной линейной

сети с двухэлементным вектором входа, значения которого находятся в интервале [-1 1]

и нулевым параметром скорости настройки, как это было для случая адаптации:

% Формирование однослойной статической линейной сети с двумя входами

% и нулевым параметром скорости настройки

net = newlin([-l 1;-1 1],1, 0, 0);

net.IWfl} = [0 0]; % Значения весов

net.b{l} = 0; % Значения смещений

Требуется обучить параметры сети так, чтобы она формировала линейную зависимость вида

t = 2p_l+p₂.

Последовательный способ. Для этого представим обучающую последовательноcnm

в виде массивов ячеек

Р = {[-1; 1] [-1/3; 1/4] [1/2; 0] [1/6; 2/3]}; % Массив векторов входа

Т = {-1 -5/12 1 1}; % Массив векторов цели

Теперь все готово к обучению сети. Будем обучать ее с помощью функции train в те чение 30 циклов.

В этом случае для обучения и настройки параметров сети используются фунции trainwb и learnwh соответственно.

% Параметр скорости настройки весов

net.inputWeights{l,1}.learnParam.lr = 0.2;

net.biases{1}.learnParam.lr = 0; % Параметр скорости настройки смещений

net.trainPararo.epochs =30; % Число циклов обучения

net1 = train(net,P,T);

Параметры сети после обучения равны следующим значениям:

W = netl.iw(1)

W = 1.9214 0.92599

у = sim(netl, P)

у = [-0.99537] [-0.40896] [0.96068] [0.93755]

ЕЕ = mse([y{:}]-[T{:}])

ЕЕ = 1.3817е-003

Зависимость величины ошибки обучения от числа циклов обучения приведена на рис. 11

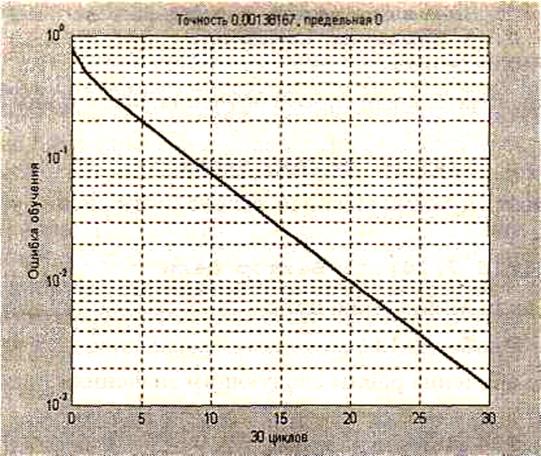
Рис. 11

Это тот же самый результат, который был получен для группового способа адаптации с использованием функции adapt.

Групповой способ. Для этого представим обучающую последовательность в виде массивов

та double array:

S = [-1 -1/3 1/2 1/6; 1 1/4 0 2/3]; Т = Е-1 -5/12 11]; netl = train(net,P,T); TRAINWB, Epoch 0/10, MSE 0.793403/0. TRAINWB, Epoch 10/10, MSE 0.00243342/0. TRAINWB, Maximum epoch reached.

Параметры сети после обучения равны следующим значениям:

W = netl.IWU}

W= 1.9214 0.92599

У = sim(netl, Р)

У = -0.99537 -0.40896 0.96068 0.93755 ЕЕ = mse(y-T)

EZ = 1.3817е-003

Этот результат полностью совпадает с результатом последовательного обучения этой же сети.

Динамиические сети. Обучение динамических сетей выполняется аналогичным образом

использованием метода train.

Последовательный способ. Обратимся к линейной модели нейронной сети с одним входом и одним элементом запаздывания.

Установим начальные условия для элемента запаздывания, весов и смещения равными 0, а параметр скорости настройки равным 0.5:

net = newlin([-l 1],1,[0 1],0.5);

Pi = {0}; % Начальное условие для элемента запаздывания

net.IW{l} = [0 0]; % Значения весов

net.biasConnect =0; % Значение смещения

net.trainParam.epochs = 22;

Чтобы применить последовательный способ обучения, представим входы и цели какмассивы ячеек:

Р = {-1/2 1/3 1/5 1/4}; % Вектор входа

Обучим сеть формировать нужный выход на основе соотношения y(t) = 2p(t) + p(t-1)тогда

Т = { -1 1/6 11/15 7/10}; % Вектор цели

Используем для этой цели М-функцию train:

netl = train(net, P, T, Pi);

Параметры сети после обучения равны следующим значениям:

W = netl.IW{l}

W = 1.9883 0.98414

у = sim(netl, P)

у = [-0.99414] [0,17069] [0.7257] [0.6939]

ЕЕ = mse([y{:}]-[T{:}])

ЕЕ = 3.6514е-005

График зависимости ошибки обучения от числа циклов приведен на рис. 12

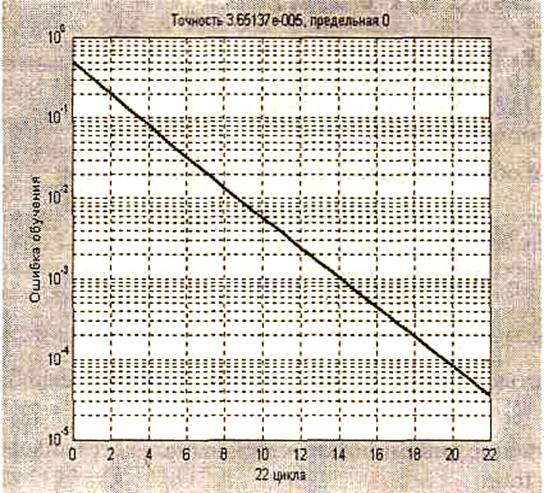
Рис. 12

Предлагаем читателю самостоятельно выполнить сравнение результатов обучения с результатами адаптации этой же сети.

Групповой способ представления обучающей последовательности для обучения динамических систем не применяется.

Методы обучения

Как только начальные веса и смещения нейронов установлены пользователем или с помощью датчика случайных чисел, сеть готова для того, чтобы начать процедуру ее обучения. Сеть может быть обучена решению различных прикладных задач - аппроксимации функций, идентификации и управления объектами, распознавания образов, классификации объектов и т. п. Процесс обучения требует набора примеров ее желаемого поведения - входов р и желаемых (целевых) выходов t; во время этого процесса веса и смещения настраиваются так, чтобы минимизировать некоторый функционал ошибки. По умолчанию в качестве такого функционала для сетей с прямой передачей сигналов принимается среднеквадратичная ошибка между векторами выхода ant. Ниже обсуждается несколько методов обучения для сетей с прямой передачей сигналов.

При обучении сети рассчитывается некоторый функционал, характеризующий качество обучения:

где J - функционал; Q - объем выборки; М - число слоев сети; q - номер выборки; S^M - число нейронов выходного слоя; а^q = [a^qM_i ] - вектор сигнала на выходе сети;

t^q = [t^qM_i ]- вектор желаемых (целевых) значений сигнала на выходе сети для выборки с номером q.

Затем с помощью того или иного метода обучения определяются значения настраиваемых параметров (весов и смещений) сети, которые обеспечивают минимальное значение функционала ошибки. Большинство методов обучения основано на вычислении градиента функционала ошибки по настраиваемым параметрам.

Обучение однослойной сети

Наиболее просто градиент функционала вычисляется для однослойных нейронных ей. В этом случае М = 1 и выражение для функционала принимает вид:

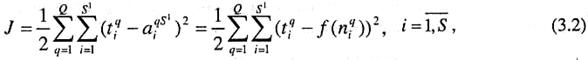
где 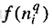- функция активации;- сигнал на входе функции активации

для i-го нейрона; 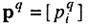- вектор входного сигнала; R - число элементов вектора входа;

число нейронов в слое; - весовые коэффициенты сети.

Включим вектор смещения в состав матрицы весов 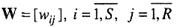, а вектор входа дополним элементом, равным 1.

Применяя правило дифференцирования сложной функции, вычислим градиент функционала ошибки, предполагая при этом, что функция активации дифференцируема:

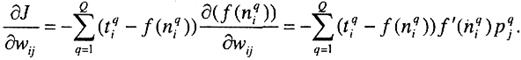(3.3)

Введем обозначение

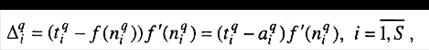
(3.4)

и преобразуем выражение (3.3) следующим образом:

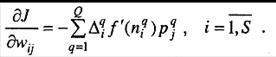
(3.5)

Полученные выражения упрощаются, если сеть линейна. Поскольку для такой сетивыполняется соотношение 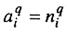, то справедливо условие. В этом случае выражение (3.3) принимает вид:

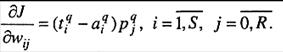
(3.6)

Выражение (3.6) положено в основу алгоритма WH, применяемого для обучениями нелинейных нейронных сетей.

Линейные сети могут быть обучены и без использования итерационных методов а путем решения следующей системы линейных уравнений:

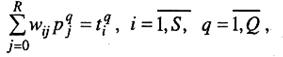
(3.7)

или в векторной форме записи:

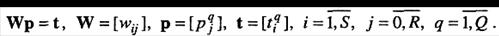
(3.8)

Если число неизвестных системы (3.7) равно числу уравнений, то такая системами может быть решена, например, методом исключения Гаусса с выбором главного элемента. Если же число уравнений превышает число неизвестных, то решение ищется с использованием метода наименьших квадратов.

⇐ Предыдущая 1 2 3 4 567 Следующая ⇒

Воспользуйтесь поиском по сайту: