 |
6.Импульс произвольной системы тел. Основное уравнение динамики поступательного движения.
|
|
|
|
6. Импульс произвольной системы тел. Основное уравнение динамики поступательного движения.
Импульс производной системы тел 
основное уравнение динамики поступательного движения 
основное уравнение динамики произвольной системы тел – результирующая всех внутренних сил, действующих на i-ое тело 
7. Замкнутая система тел. Импульс системы. Закон сохранения импульса системы тел. Центр инерции.
Замкнутая система – такая система в которой система тел взаимодействует только между собой.
замкнутая система – изолированная если на нее не действуют внешние силы, то есть она не взаимодействует с внешними телами
импульс замкнутой системы не изменяется во времени
ЗСИ p=const
скорость центра инерции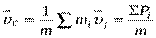 
8. Виды и категории сил в природе. 4 типа взаимодействий.
В настоящее время различают 4 типа взаимодействия: гравитационные, электростатические, сильные (ответственные за связь частиц в ядрах) слабые (ответственные за распад частиц)
9. Сила тяжести и вес тела (сходство, различие и равенство). Состояние невесомости.
Сила тяжести и вес тела относятся к гравитационным силам F=mg. Вес и сила равны друг другу но они приложены к разным точкам: вес – к опоре, сила тяжести – к самому телу P=mg±ma; P=m(g±a). При a=g наступает невесомость.
10. Упругие силы. Загон Гука для пружины и стержня. Модуль Юнга, коэффициент Пуассона.
Под действием внешних сил возникают деформации (т. е. изменения размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, которое называется пределом упругости. При превышении этого предела деформация становится пластической. В этом случае после устранения внешних сил первоначальные форма и размеры тела полностью не восстанавливаются.
|
|
|
Удлинение пружины пропорционально внешней силе и определяется законом Гука:
Fвн – какая0либо действующая внешняя сила.
k – жесткость пружины. Видно, что чем больше k, тем меньшее удлинение получит пружина под действием данной силы.
Для тонкого растяжимого стержня закон Гука имеет вид:
F=k∆ l{\displaystyle F=k\Delta l. }
Здесь {\displaystyle F} F— сила, которой растягивают (сжимают) стержень, ∆ l {\displaystyle \Delta l} — абсолютное удлинение (сжатие) стержня, а {\displaystyle k}KK k-коэффициент упругости (или жёсткости).
Мо́ дуль Ю́ нга (модуль продольной упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению, сжатию при упругой деформации.
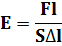
F — нормальная составляющая силы, {\displaysS — площадь поверхности, по которой распределено действие силы, {\displaystyle l — длина деформируемого стержня, {\displaystyle \Delta l} 
— модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина {\displaystyle l}l).
Отношение абсолютного значения относительного поперечного сжатия к относительной продольной деформации называется коэффициентом Пуассона
11. Деформация сдвига. Относительный сдвиг. Модуль сдвига. Тангенциальное напряжение.
Деформация сдвига. Деформация сжатия аналогична рассмотренной деформации растяжения. Силы, деформирующие брус при сжатии, направлены вдоль оси бруса, но навстречу друг другу. Величина действительных напряжений при сжатии σ сж=N: F, где N - равнодействующая внутренних сил упругости (продольная сила).
Угол γ, на который изменился прямой угол параллелепипеда, называется относительным сдвигом и является мерой сдвига, т. е. относительный сдвиг - есть отношение абсолютного сдвига к расстоянию между рассматриваемыми сдвигаемыми сечениями.
|
|
|
Модуль сдвига — физическая величина, характеризующая способность материала сопротивляться сдвиговой деформации.
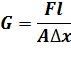
F — площадь, на которую действует сила; A{\displaystyle \gamma _{xy}=\Delta x/I=tg\theta }aA — сдвиговая деформация; 
{\displaystyle \Delta x} — смещение; {\displaystyle I}LLlll — начальная длина.
Величина, равная отношению силы к величине поверхности, на которую сила действует, называется напряжением. Если сила направлена по нормали к поверхности, напряжение называется нормальным. Если сила направлена по касательной к поверхности, на которую она действует, напряжение называется тангенциальным. Нормальное напряжение принято обозначать буквой σ, тангенциальное — буквой τ.
Где S-площадь соответствующей грани, f-сила
|
|
|
