 |
19. Основное уравнение динамики вращательного движения твердого тела относительно точки. Момент сил. Момент импульса. Момент инерции.
|
|
|
|
19. Основное уравнение динамики вращательного движения твердого тела относительно точки. Момент сил. Момент импульса. Момент инерции.
Основного уравнения динамики вращательного движения: изменение момента количества движения твердого тела 
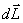, равно импульсу момента 
всех внешних сил, действующих на это тело.
Момент силы – это произведение силы на плечо этой силы. М=Fl
Моме́ нт и́ мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение
L=[ 
]
Моме́ нт ине́ рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
20. Основное уравнение динамики вращательного движения твердого тела относительно оси. Момент сил. Момент импульса. Момент инерции. Закон сохранения момента импульса как следствие симметрии пространства – времени.
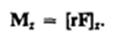Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z
Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси.
|
|
|
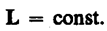
(19. 4)
Выражение (19. 4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Закон сохранения момента импульса — фундаментальный закон природы. Он связан со свойством симметрии пространства — его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета
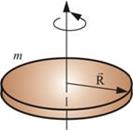
21. Расчёт моментов инерции сложных и простых тел. Теорема Штейнера. Момент инерции стержня (вывод формулы с помощью теоремы Штейнера).
| 
| 
|
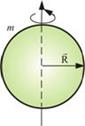
Шар: k = 2/5,  Сфера: 
| Диск: k = 1/2,  Обруч: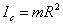 
| Стержень: 
|
Момент инерции сложной фигуры равен сумме моментов инерции ее составных частей
Это непостредственно следует из свойств определенного инетеграла
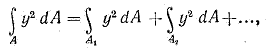
где А = А1 + А2 +...
Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее на ряд простых фигур, вычислить моменты инерции этих фигур и затем просуммировать эти моменты инерции
Момент инерции тела относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс С тела, плюс произведение массы тела на квадрат расстояния между осями.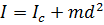 
В общем случае моменты инерции различных тел можно найти по формуле
I= mR2,
где - коэффициент пропорциональности, который зависит от формы тела и его расположения относительно оси вращения.
Найдем момент инерции однородного стержня относительно оси, проходящей через один из его концов, перпендикулярно продольной геометрической оси симметрии (рис. 5. 2).
Рис. 5. 2
Пусть ось вращения ВВ проходит через правый конец стержня (точка Г), тогда
I= mL2,
где L - длина стержня.
Согласно теореме Штейнера имеем -
.
Величину момента инерции Ic относительно оси, проходящей через центр масс (точка С), представим как сумму моментов инерции двух стержней с длинами ДС=СГ=L / 2и массой каждого, равной m/2 стержня, т. е.
|
|
|
Подставим значения момента инерции I и Ic в формулу теоремы Штейнера и найдем :
После преобразования получим, что = 1/3.
Следовательно, момент инерции стержня относительно оси, проходящей через центр масс,
а относительно оси ВВ,
|
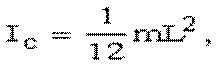
22. Кинетическая энергия вращающегося тела. Законы сохранения и их связь с симметрией пространства и времени.
Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить.
|
|
|
