 |
46. Основное уравнение динамики гармонических колебаний. Решение уравнения.
|
|
|
|
46. Основное уравнение динамики гармонических колебаний. Решение уравнения.
Второй закон Ньютона позволяет, в общем виде, записать связь между силой и ускорением, при прямолинейных гармонических колебаниях материальной точки (или тела) с массой m.
Т. к. исходя из второго закона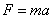 
, можно записать:
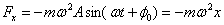
где Fx – проекция силы на направление х. Из формулы следует, что сила F пропорциональна х и всегда направлена к положению равновесия (поэтому ее и называют возвращающей силой). Период и фаза силы совпадают с периодом и фазой ускорения.
Примером сил удовлетворяющих формуле являются упругие силы. Силы же, имеющие иную природу, но удовлетворяющие ф-ле, называются квазиупругими. Квазиупругая сила:
где k – коэффициент квазиупругой силы.
Сравнивая ф-лы, видим, что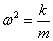 
.
В случае прямолинейных колебаний вдоль оси х, проекция ускорения на эту ось 
.
Подставив выражения для ax и Fx во второй закон Ньютона, получим основное уравнение динамики гармонических колебаний, вызываемых упругими или квазиупругими силами:
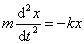или 
; 
, тогда
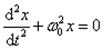
Решением этого уравнения всегда будет выражение вида:
, т. е. смещение груза под действием упругой или квазиупругой силы является гармоническим колебанием, происходящим по синусоидальному закону.
Круговая частота незатухающих колебаний 
, но, т. к. 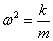, тогда, отсюда
то есть чем больше жесткость пружины k, тем меньше период (больше частота), а чем больше масса, тем период колебаний больше.
47. Маятники математический и физический, пружинный. Их уравнения движения.
Математический маятник - это материальная точка, подвешенная на тонкой нерастяжимой и невесомой нити.
Период колебаний математического маятника зависит от его длины, определяется по формуле
|
|
|
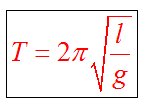
Пружинный маятник - это груз, прикрепленный к пружине, массой которой можно пренебречь.
Пока пружина не деформирована, сила упругости на тело не действует. В пружинном маятнике колебания совершаются под действием силы упругости.
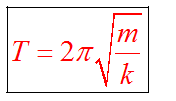
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
Тогда период колебаний математического маятника будет равен:
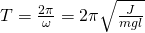
48. Затухающие колебания. Частота собственных колебаний ω 0, затухающих колебаний ω, условный период Тусл.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Период затухающих колебаний вычисляют по формуле
Частота собственных колебаний:
Частота затухающих колебаний ω:
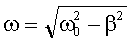
49. Коэффициент затухания, декремент затухания, добротность. Апериодический процесс.
Коэффициент затухания:
колеблющегося тела
где r - коэффициент сопротивления среды, m - масса тела;
колебательного контура
где R - активное сопротивление,
L - индуктивность контура.
Декремент затухания - количественнаяхарактеристика быстроты затухания колебаний в линейной системе; представляет собой натуральныйлогарифм отношения двух последующих максимальных отклонений колеблющейся величины в одну и ту жесторону. T. к. в линейной системе колеблющаяся величина изменяется по закону
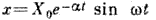(где постоянная величина 
- коэф. затухания) и два последующих наиб. отклонения в одну сторону X1 и X2(условно наз. " амплитудами" колебаний) разделены промежутком времени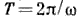 
(условно наз. " периодом" колебаний), то 
, а Д. з. 
.
Добро́ тность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан. Обозначается символом Q.
|
|
|
Общая формула для добротности любой колебательной системы:
Апериодический процесс - переходный процесс в динамич. системе, при к-ром выходная величина, характеризующая переход системы от одного состояния к другому, либо монотонно стремится к установившемуся значению, либо имеет один экстремум (см. рис. ). Теоретически может длиться бесконечно большое время. А. п. имеют место, напр., в системах автоматич. управления.
Графики апериодических процессов изменения параметра x(t) системы во времени: хуст - установившееся (предельное) значение параметра.
|
|
|
