 |
Определение рабочих отметок вершин.
|
|
|
|
Осуществляем по формуле: hi= Hki-Hi, м (4.7)
Например, для вершины 2 (рисунок 4.5) рабочая отметка равна:
h2=18,56-16,7=1,86 м
Если hi меньше 0, значит мы имеем дело с выемкой, если же hi>0 – с насыпью.
Построение линии нулевых работ (л.н.р.)
Л.н.р. представляет собой линию пересечения проектной плоскости с поверхностью земли. Л.н.р. пресекает ту сторону квадрата или треугольника, на концах которой рабочие отметки имеют разный знак. Положение л.н.р. на стороне квадрата или треугольника определяется по формуле:
, м (4.8)
где: ℓi-j – расстояние от вершины с номером i до точки, принадлежащей л.н.р., м;
hi – рабочая отметка вершины с номером i, м;
hj – рабочая отметка вершины j на другом конце пересекаемой л.н.р. стороны, м;
b – длина стороны квадрата или треугольника ("а" или "а 
", если пересекается диагональ), м.
Например, для стороны 3-4 (рисунок 4.5):
При построении л.н.р. полученные на сторонах точки соединяются между собой прямыми (рисунок 4.5).
Рисунок 4.5. Схема к определению красных, рабочих отметок и построению л.н.р.
Определение частных объемов.
Определение частных объемов целых квадратов и треугольников (не пересекаемых л.н.р.)
а) при определении объемов способом квадратных призм (рисунок 4.6):
Рисунок 4.6. Схема целого квадрата.
|  (4.9)
где: h1, h2, h3, h4 – рабочие отметки в вершинах квадрата, м;
а – длина стороны квадрата, м.
Для квадрата №1 на рисунке 4.12:
|
б) при определении объемов способом треугольных призм (рисунок 4.7):
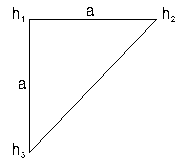Рисунок 4.7. Схема целого треугольника.
|  (4.10)
где: h1, h2, h3 – рабочие отметки в вершинах треугольника, м.
|
Определение объемов переходных квадратов и треугольников, пересекаемых л.н.р.
|
|
|
а) при определении объемов способом квадратных призм.
При переходном квадрате 1-го типа (рисунок 4.8) вначале по формуле (4.9) находим балансовый объем Vn. Затем находим объем треугольной части квадрата по формуле:
Рисунок 4.8. Схема переходного квадрата 1-го типа.
|  (4.11)
где: h1 – рабочая отметка вершины, принадлежащей треугольной части квадрата, м;
h2, h3 – рабочие отметки вершин, располагаемых по сторонам квадрата напротив вершины с отметкой h1, м.
На заключительном этапе находим объем пятиугольной части квадрата Vn5:
 Vn5 = Vn – Vn3, м3 (4.12)
|
Для квадрата №2 на рисунке 4.12 объемы равны:
При переходном квадрате 2-го типа (рисунок 4.9) объемы насыпи и выемки определяются по выражениям:
Рисунок 4.9. Схема переходного квадрата 2-го типа.
|  (4.13)
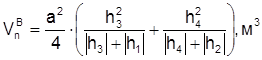 (4.14)
В выражениях (4.13, 4.14) знак объема определяется знаком рабочих отметок в числителе.
|
Для квадрата №4 объемы выемки и насыпи равны (рисунок 4.12):
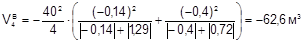
б) при определении объемов способом треугольных призм.
Рисунок 4.10. Схема переходного треугольника.
| Вначале по формуле (4.10) находим балансовый объем Vn. Затем находим объем треугольной части треугольника:
 , м3 (4.15)
Объем четырехугольной части треугольника равен:
Vn4 = Vn – Vn3, м3 (4.16)
В формулах "n" – номер квадрата или треугольника.
|
Определение объемов земляных масс удобнее всего производить в табличной форме:
Таблица 4.2. Объемы земляных масс площадки.
| № квадрата (треугольника) | Рабочие отметки вершин, м | Объем: V = F•hср, м3 | |||||
| h1 | h2 | h3 | h4 | hCP | Выемка (–) | Насыпь (+) | |
| ∑V (–) | ∑V (+) |
Примечание: Для способа квадратных призм F=a2, для треугольных призм – F=a2/2, h4=0.
Построение линии откосов
Откосы устраиваются с целью обеспечения устойчивости планировочной площадки, как разновидности постоянного земляного сооружения. Угол откоса постоянных земляных сооружений принимается не более угла естественного откоса (таблица 4.3).
|
|
|
Таблица 4.3. Значения m для постоянных выемок и насыпей.
| Состояние грунта | Грунт | ||||||
| песок | супесь | суглинок | глина | ||||
| мелко-зернистый | среднезернистый | крупно-зернистый | легкий | средний | |||
| Сухой | 2,25 | 2,0 | 1,75 | 1,75 | 1,25 | 0,75 | 1,0 |
| Влажный | 1,75 | 1,5 | 1,5 | 1,75 | 1,75 | 1,25 | 1,5 |
| Мокрый | 2,75 | 2,25 | 2,0 | 2,75 | 2,75 | 4,75 | 3,75 |
Рисунок 4.11. Схема к определению заложения откосов.
| Принимаем, что за пределами строительной площадки поверхность земли горизонтальна (рисунок 4.11), в этом случае заложение откоса в каждой из вершин треугольников или квадратов по контуру площадки определяется по формуле: А=m•h, м (4.17) где: m – коэффициент откоса, принимаемый равным ctg угла естественного откоса по таблице 4.3; h – рабочая отметка, м. |
Для построения линии откосов по контуру площадки откладываем в вершинах вычисленные заложения и полученные точки соединяем прямыми (рисунок 4.12).
|
|
|
