 |
2.11.3.1. Счетчик с последовательным переносом
|
|
|
|
2. 11. 3. 1. Счетчик с последовательным переносом
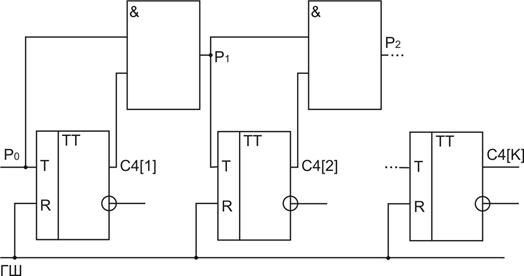
Рис. 2. 60. Двоичный суммирующий счетчик с последовательным переносом асинхронного типа.
На рис. 2. 60 и 2. 61 приведены схема и УГО двоичного суммирующего счетчика с последовательным переносом асинхронного типа.
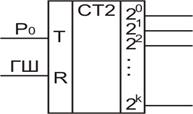
Рис. 2. 61. УГО счетчика
Ниже показана МОДИС- модель этого счетчика и временная диаграмма работы счетчика (рис. 2. 62).
Составим МОДИС- модель этого счетчика.
Описание переменных
‘ЗАВИСИМ’ С4 [1: K], Р [1: 2];
‘ИНЕЗАВ’ Р0, ГШ;
Описание схемы
С4 [1] ’: =‘ ‘ЕСЛИ’ ГШ ‘ТО’ 0
‘ИНЕСЛИ’ Р0 ‘ТО’ IC4 [1]
‘ИНАЧЕ’ C4 [1];
Р1 ‘: =‘ C4 [1] * P0
С4 [1: K] ‘: =‘ ‘ЕСЛИ’ ГШ ‘ТО’ 0
‘ИНЕСЛИ’ Р0 ‘ТО’ C4 [1: K]+1
“ИНАЧЕ’ C4 [1: K];
Каждый разряд счетчика делит частоту поступающих на его вход импульсов на 2. У асинхронного счетчика моменты срабатывания
отдельных разрядов счетчика определяются реальными задержками в схемах формирования переноса.
τ p - время формирования переноса в одном разряде.
Быстродействие счетчика определяется временем пробега переноса по всем разрядам.
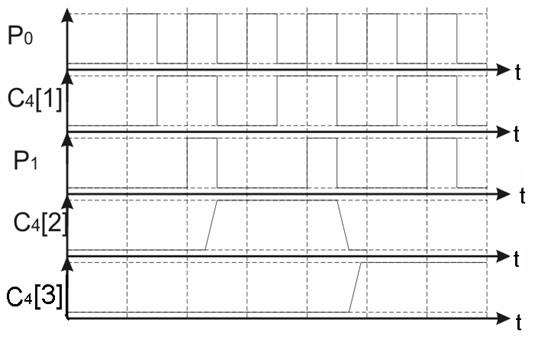
Рис. 2. 62. Временная диаграмма работы счетчика
Трег= n * τ p – время регистрации – интервал времени от момента поступления на вход счетчика очередного импульса до момента, когда новое значение установится во всех разрядах счетчика.
n –количество разрядов в счетчике.
2. 11. 3. 2. Счетчик с параллельным переносом
Как следует из рис. 2. 63 счетчик является синхронным, так как срабатывание всех триггеров происходит практически одновременно при поступлении на его вход сигнала Р0. Схемы формирования переносов строятся по следующим формулам:
|
|
|
Р1 ‘: =‘ Р0 * Q1;
Р2 ‘: =‘ P1 * Q2 = P0 * Q1 * Q2;
... Pк ‘: =’ P0 * Q1 * Q2 *... * Qk-1; Трег≈ τ p.
Счетчики с параллельным переносом обладают наибольшим быстродействием, причем Трег теоретически не зависит от количества разрядов. Однако на практике такие счетчики строятся не более, чем на 8 разрядов.
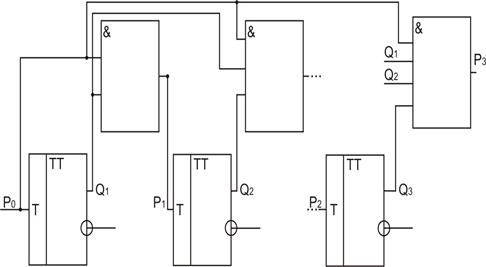
Рис. 2. 63. Счетчик с параллельным переносом
2. 11. 3. 3. Счетчик с групповым переносом
Для повышения быстродействия счетчиков с большим количеством разрядов применяют схемы с групповым переносом.
В схеме на рис. 2. 64 принято, что внутри группы [1: К] разрядов перенос организован последовательным способом, а между группами – параллельным.

Рис. 2. 64. Двоичный счетчик с групповым переносом
Полное количество разрядов в счетчике n =КL, где К – число разрядов в группе, L- количество групп.
τ p – время формирования группового переноса или переноса между разрядами.
Время регистрации счетчика Трег = τ p (K + L – 1).
2. 11. 3. 4. Реверсивный счетчик
Реверсивный счетчик обеспечивает, как суммирование, так и вычитание импульсов из содержимого счетчика.
Существуют две основные структуры реверсивных счетчиков:
1) на вход схемы подается одна последовательность входных импульсов, но в каждый момент времени известен ее знак или режим работы счетчика,
2) на вход реверсивного счетчика поступают две последовательности импульсов с разными знаками.
Схема, представленная на рис. 2. 65, соответствует первой структуре. На вход схемы поступает одна последовательность сигналов. Триггер знака ТЗн определяет режим работы счетчика.
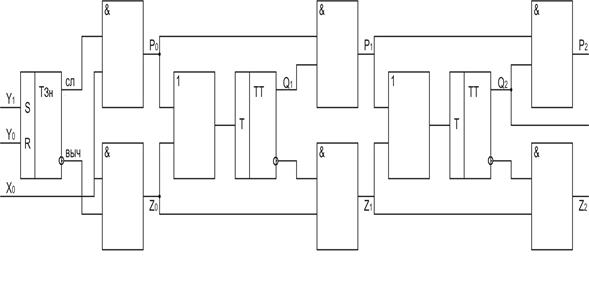
 Рис. 2. 65. Реверсивный счетчик
Рис. 2. 65. Реверсивный счетчик
В режиме сложения формируется входной сигнал с положительным знаком и последовательность переносов
P0 ’: =‘ ТЗн * X0 ;
в режиме вычитания - последовательность заемов
Z0 ‘: =‘ IТЗн * X0;
таким образом, на входе первого триггера Q1 появляются две последовательности сигналов с разными знаками, что соответствует второй структуре. На рис. 2. 65 показано УГО реверсивного счетчика этого типа.
|
|
|
Составим МОДИС-описание схемы счетчика, примем, что он состоит из восьми разрядов.
Q1 ‘: =‘ ‘ЕСЛИ’ Р0 V Z0 ‘ТО’ IQ1 ‘ИНАЧЕ’ Q1 ;
P1 ‘: =‘ Q1 * P0; Z  ‘: =’ IQ1 * Z
‘: =’ IQ1 * Z  ;
;
Q [1: 8] ’: =‘ ‘ЕСЛИ’ ТЗн * X0 ‘ТО’ Q[1: 8] + 1
‘ИНЕСЛИ’ IТЗн * X0 ‘ТО‘ Q[1: 8] – 1
‘ИНАЧЕ’ Q [1: 8];
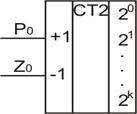
Рис. 2. 66. УГО реверсивного счетчика
|
|
|


