Вычисление определителя методом Гаусса

Вычисление определителя методом Гаусса

 

Вычислим определитель методом Гаусса.

Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.

Идея метода состоит в следующем: пусть дан определитель третьего порядка

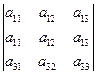                           (1)

элемент 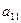 должен быть равен , для этого первую строку разделим на .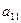

 Получим определитель вида                       (2)

Обнулим элементы, стоящие в первом столбце, кроме первого. Для этого из второй строки вычтем первую, умноженную на , далее из третьей строки вычтем первую, умноженную на . Получим определитель вида .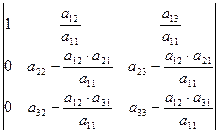

Обозначим его элементы буквой с, тогда

                                                            (3)

Теперь надо обнулить элемент . Элемент  должен быть равен , для этого вторую строку разделим на . Получим определитель вида .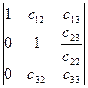

Далее из третьей строки вычтем вторую, умноженную на .

.

Обозначим его элементы буквой t, тогда

                                                 (4)

Вот мы привели определитель к треугольному виду, теперь он равен .

Разберем теперь это на конкретном примере.

Пример 4: Вычислить определитель  методом Гаусса.

Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).

Получили

 Из второй строки вычтем первую, умноженную на 2, далее из третьей строки вычтем первую, умноженную на 3. Получили  

Далее из третьей строки вычтем вторую, умноженную на 3.

 Получили -

§2. Матрицы

Виды матриц

Определение 7: Если в матрице m строк и n столбцов, то она называется размерностью m 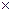n и пишут .

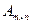Определение 8: Если 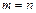, то матрица называется квадратной.

Определение 9: Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).

Определение 10: Матрица, состоящая из нулей, называется нулевой матрицей.

Определение 11: Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.

Определение 12: Единичной матрицей называется диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице.

  Определение 13: Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.

Действия над матрицами.

Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.

Пример 5:  

Матрицы А и В равны, т. е.

Определение 15: Суммой (разностью) матриц А и В называется такая матрица С, у которой каждый элемент равен .

Пример 6: Найти матрицу 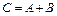, если

Решение: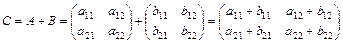

Cвойства сложения

А+В=В+А(переместительное)

 

2⁰ А+О=А, где О-нулевая матрица

 

3⁰  А+(В+С)=(А+В)+С (дистрибутивное)

 

4⁰ А+(-А)=О, где – А противоположная матрица

 (т. е. элементы имеют противоположные знаки)

Определение 16: Произведением матрицы А на число 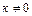 называется матрица, полученная из данной умножением всех ее элементов на число .

Пример 7:

умножение матиц

Это действие распространяется на так называемые согласованные матрицы.

Определение 17: Матрица А называетсясогласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.

Пример 8:  и 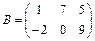 - согласованные

 и  - несогласованные

 и 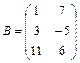 несогласованные

Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементов i строки матрицы А на соответствующие элементы j-го столбца матрицы В.

 

Если матрица А имеет размерность 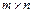, а матрица В , то .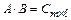

Пример 9: Умножить матрицы

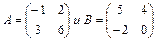
⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: