 |
Обратная матрица. Алгоритм нахождения обратной матрицы. §3. Матричная запись и матричное решение систем линейных уравнений.
|
|
|
|
Обратная матрица
Определение 19: Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной матрицей относительно данной, и обозначается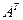 
.
Пример 10: 
Пример 11: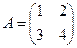 
Определение 20: Обратнoй матрицей к квадратной
матрице А называется квадратная матрица 
,
удовлетворяющая условию 
.
Действия умножения матриц, в общем случае,
не подчиняется переместительному закону распределения, т. е. 
Теорема: Для того, чтобы квадратная матрица А имела себе обратную необходимо и достаточно, чтобы матрица А была не вырожденная, т. е. определитель отличен от нуля.
Алгоритм нахождения обратной матрицы
1. 
2. транспонировать матрицу А
3. вычислить алгебраические дополнения всех элементов транспонированной матрицы
4. составляем матрицу А*(союзная или присоединенная)
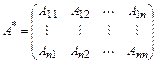
5. 
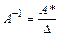
Пример 12: Найти обратную матрицу для матрицы
А= 
Решение: Т. к. определитель равен 
, то обратная матрица имеет место быть.
Транспонируем матрицу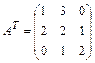 
Вычислим все алгебраические дополнения
транспонированной матрицы
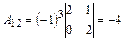
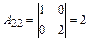
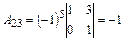
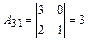
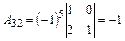
Т. о. союзная матрица имеет вид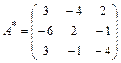 
Обратная матрица имеет вид 
.
Замечание: иногда обратную матрицу записывают 
.
Пример 13: При каких значениях l матрица не имеет обратную? 
Решение: Если определитель матрицы равен нулю, то такая матрица не имеет обратной. Нужно вычислить определитель данной матрицы и приравнять его к нулю. Получим уравнение первого порядка, из которого и найдем значение 
или 
следовательно 
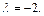
Пример 14: При каких значениях l матрицы
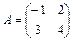и 
перестановочны?
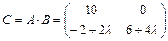
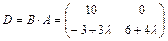
Сравнив матрицы С и D, находим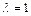 
.
|
|
|
Пример 15: Вычислить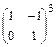 
Найдем матрицу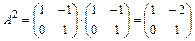 
Затем найдем матрицу 
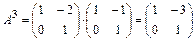
§3. Матричная запись и матричное решение систем линейных уравнений.
Пусть дана 
(6)
, где матрица А= 
- основная матрица системы.
Х=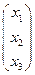 
- матрица-столбец неизвестных
В= 
- матрица-столбец свободных членов.
Очевидно 
(7) - матричное уравнение системы.
Если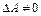 
, то система (7) решается следующим образом
. Перепишем его в другом виде
(т. к. 
- единичная матрица), то
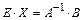(т. к. 
), то 
- решение системы (7)
Пример 16: Решить систему матричным методом
Решение: А= В= 
Х=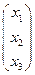
Т. к. обратная матрица уже найдена в примере№12, то
= 
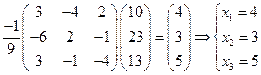
Пример 17: Решить матричное уравнение:
Решение: Составим это уравнение в буквенной форме
, его решение разобрано чуть выше.
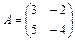
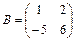
Найдем обратную для матрицы А.
, т. к. , то 
.
§4. Системы линейных уравнений.
Определение 21: Системой m линейных уравнений с n неизвестными 
называется система вида:
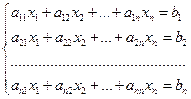(6)
, где 
- коэффициенты при неизвестных (числа);
- свободные коэффициенты (числа).
Система линейная, т. к. все иксы в первой степени.
Определение 22: Линейная система (6) называется неоднородной, если среди свободных коэффициентов хотя бы один отличен от нуля. Если все свободные коэффициенты равны нулю, то система называется однородной.
Определение 23: Решением линейной системы (6) называется упорядоченная совокупность чисел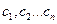 
подстановка которых вместо обращает в тождество каждое из уравнений системы.
Определение 24: Система, имеющая хотя бы одно решение, называется совместной. Система, не имеющая ни одного решения, называется несовместной.
Формулы Крамера.
Рассмотрим систему
Определение 25: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы.
|
|
|
Составим определитель Δ 1= 
Назовем его первый вспомогательный определитель системы. Аналогично
Δ 2=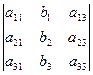 
и Δ 3= 
.
- называются формулы Крамера (8)
Замечание: Формулы Крамера верны и для системы n-го порядка, но только для квадратной системы.
|
|
|
