 |
Однородная система. Метод Гаусса.. Вариант 1
|
|
|
|
Однородная система.
Теорема 1. Однородная система всегда совместна.
Теорема 2. Для того, чтобыоднородная система имела не нулевое решение необходимо и достаточно, чтобы ее определитель равнялся нулю
Следствие: Для того, чтобы однородная система имела не нулевое решение необходимо и достаточно, чтобы 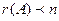 .
.
Пример 21: Исследовать однородную систему: 
Решение: 




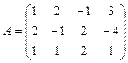 ~
~  ~
~  ~
~ 
Система имеет  множество решений, базисные неизвестные
множество решений, базисные неизвестные 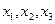 и
и  - свободная переменная равна с.
- свободная переменная равна с.  или
или 
Метод Гаусса.
Пусть дана система №9. Идея метода состоит в следующем: пусть коэффициент при  в первом уравнении системы №1
в первом уравнении системы №1  .
.
1) Исключим неизвестное  из всех уравнений системы, кроме первого. Для этого прежде всего разделим обе части уравнения сист-мы№1 на коэффициент
из всех уравнений системы, кроме первого. Для этого прежде всего разделим обе части уравнения сист-мы№1 на коэффициент 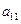 . Получим новую систему, равносильную данной.
. Получим новую систему, равносильную данной.
2) Умножим первое уравнение на  и вычтем его из второго уравнения системы; затем умножим первое уравнение на
и вычтем его из второго уравнения системы; затем умножим первое уравнение на 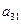 и вычтем его из третьего уравнения и т. д. В результате этого шага приходим к системе вида №2:
и вычтем его из третьего уравнения и т. д. В результате этого шага приходим к системе вида №2:
 , где
, где 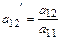 ---(10)
---(10)
3) Исключим 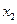 из всех уравнений системы №2, кроме первого и второго. Для этого разделим обе части второго уравнения системы №2 на
из всех уравнений системы №2, кроме первого и второго. Для этого разделим обе части второго уравнения системы №2 на  ; затем умножим второе уравнение последовательно на
; затем умножим второе уравнение последовательно на 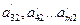 и вычтем поочередно из соответствующих уравнений, кроме 1-го и 2-го.
и вычтем поочередно из соответствующих уравнений, кроме 1-го и 2-го.
4) Продолжая этот процесс далее, мы придем либо к системе вида:
 --- (11) в случае ее совместности, либо к системе вида:
--- (11) в случае ее совместности, либо к системе вида:
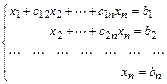 ---(12)
---(12)
5) система вида (11) называется ступенчатой, система вида (12) – треугольной. В случае системы (12) из последнего уравнения определяется 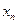 , подставляется в предыдущее уравнение системы (12), определяем
, подставляется в предыдущее уравнение системы (12), определяем  неизвестное и т. д. из 1-го уравнения найдем
неизвестное и т. д. из 1-го уравнения найдем  неизвестное.
неизвестное.
|
|
|
В случае системы (11) имеем систему совместную, но не определенную, которая имеет  множество решений. Выделяем базисный минор и базисные неизвестные, остальные неизвестные назовем свободные и приведем систему (11) к виду (12).
множество решений. Выделяем базисный минор и базисные неизвестные, остальные неизвестные назовем свободные и приведем систему (11) к виду (12).
Все выше указанные описания на практике производят над матрицами, составленными из коэффициентов перед неизвестными и столбца свободных коэффициентов.
Пример 22: 1) Исследовать систему, и в случае ее совместности найти решение 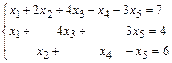
Решение:  ~
~ 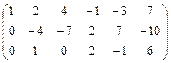 ~
~
 ~
~ 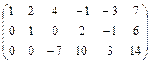

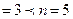
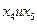 - свободные переменные
- свободные переменные
последней матрице соответствует система 
равносильная исходной 
Вариант 1
А1. Вычислить определитель:
а) 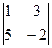 б)
б)  .
.
А2. Решить уравнение:
 .
.
А3. Вычислить определитель, пользуясь правилом треугольника:
 .
.
А4. Найти алгеброические дополнения элементов  и
и  определителя (см. задачу А3).
определителя (см. задачу А3).
А5. Вычислить определитель, используя подходящее разложение по строке или столбцу:  .
.
А6. Решить систему уравнений с помощью правила Крамера.
а) 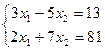
| б) 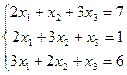
|
А7. Найти матрицу 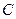 , полученную путем преобразований матриц
, полученную путем преобразований матриц  и
и  :
:
 .
.
 ;
; 
А8. Вычислить: 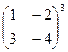 .
.
А9. При каких значениях  матрица не имеет обратную?
матрица не имеет обратную?

А10. Решить матричное уравнение: 
А11. При каких значениях  матрица имеет ранг, равный 1?
матрица имеет ранг, равный 1?

В1. Вычислить определитель, предварительно обратив в нуль все, кроме одного, элемента какой-либо строки (столбца):
 .
.
В2. Вычислить определитель приведением их методом Гаусса к треугольному виду.
а) 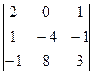
| б) 
|
В3. Умножить матрицы:
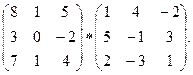
В4. При каких значениях  матрицы перестановочны?
матрицы перестановочны?
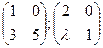
В5. Найти обратную матрицу:
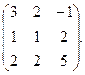
В6. Найти ранг матрицы методом Гаусса:
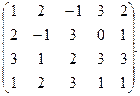
В7. Решить методом Гаусса систему уравнений:
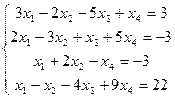 .
.
С1. Умножить матрицы:
 .
.
С2. Решить матричным методом систему уравнений из задачи А6 (б).
|
|
|
С3. Решить методом Гаусса системы уравнений:
а) 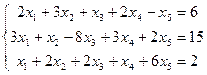 , ,
| б) 
|
в)  . .
|
|
|
|


