 |
Количественные методы описания систем
|
|
|
|
Количественные методы (методы формализованного представления систем) используются, прежде всего, для анализа и количественной оценки вариантов, описания законов их функционирования, установления связи показателей эффективности и основных факторов влияния, определения точности, корректности используемых моделей систем. К подобным методам относят [1, 3 – 7]:
- аналитические методы (методы классической математики, включая интегральное и дифференциальное исчисления, методы поиска экстремумов функций, вариационное исчисление и т.д.; методы математического программирования, методы многокритериальной оптимизации, методы теории игр и др.);
- статистические методы (теория вероятностей, математическая статистика, корреляционно-регрессионный и дисперсионный анализ, факторный и компонентный анализ, теория временных рядов и др.; направления прикладной математики, использующие стохастические представления – теорию массового обслуживания, методы статистических испытаний (основанные на методе Монте-Карло), методы выдвижения и проверки статистических гипотез А. Вальда и другие методы статистического имитационного моделирования);
- теоретико-множественные методы (общая теория абстрактных множеств, реляционная алгебра, теория категорий, теория нечетких множеств и т. п.);
- графические методы (теория графов, методы сетевого планирования, разнообразные методики графического отображения объектов и процессов);
- логико-математические методы (алгебра логики, теория абстрактных автоматов, методы логического анализа и вывода и др.);
- лингвистические методы (теория формальных грамматик, методы структурно- лингвистического анализа и пр.).
|
|
|
Теоретико-множественные, логические, лингвистические, семиотические представления основаны на методах дискретной математики и составляют теоретическую основу разработки языков моделирования, автоматизации проектирования, информационно-поисковых языков и т.п.
Приведенная классификация, выделяющая качественные и количественные методы, как и любая другая, является условной, так как методы использования опыта и активизации интуиции специалистов часто в той или иной степени используют формализованные представления (статистический анализ данных, графическое описание задачи и т. п.).
Рассмотрим подробнее, например, аналитические методы.
Аналитическими в рассматриваемой классификации названы методы, которые отображают реальные объекты и процессы в виде точек, совершающих какие-либо перемещения в пространстве или взаимодействующие между собой, т.е. сложная система преобразуется в точку, совершающую какое-то движение (или обладающую каким-то поведением), посредством оператора (функции, функционала). Причем поведение точек, их взаимодействие описывается строгими соотношениями, имеющими силу закона.
Аналитические методы используются как в классическом математическом анализе(методы исследования функций, их вида, способов представления, поиска экстремумов функций и т.д.), так и в разделах современной математики, таких как математическое программирование (линейное, нелинейное, динамическое и т.д.), теория игр (матричные игры с чистыми стратегиями, дифференциальные игры и т.д.).
Большинство из направлений математики не содержит средств постановки задачи и доказательства адекватности модели, которая чаще всего доказывается экспериментально, но это дорого и не всегда реализуемо.
Математическое же программирование содержит средства постановки задачи и методы решения слабо формализованных задач (планирования, распределения работ и ресурсов, загрузки оборудования и т.д.).
|
|
|
Рассмотрим пример постановки задачи математического программирования. Для изготовления различных изделий А, В и С предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида – aij, 
, цена одного изделия А, В и С – cj, 
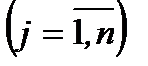, общее количество сырья каждого вида – bi, 
, которое может быть использовано предприятием, приведены в таблице 4.1.
Таблица 4.1 – Исходные данные задачи
| Вид сырья | Нормы затрат сырья (кг) на одно изделие, aij | Общее количество сырья (кг), bi | ||
| А | В | С | ||
| S 1 | ||||
| S 2 | ||||
| S 3 | ||||
| Цена одного изделия (руб.), cj |
Необходимо составить такой план производства изделий, при котором общая стоимость произведенной предприятием продукции является максимальной, учитывая, что изделия А, В и С могут производиться в любых количествах, а производство ограничено запасами сырья.
Составим математическую модель этой задачи. Пусть необходимо выпустить изделий А в количестве x 1 штук, изделий В – x 2, изделий С – x 3. Учитывая, что стоимость каждого вида изделий известна, запишем выражение целевой функции, представляющей собой общую стоимость произведенной предприятием продукции, в виде:
| (4.1) |
Необходимо найти максимум этой функции при ограничениях, которые запишем в виде системы неравенств, так как количество сырья каждого вида ограничено:
| (4.2) |
Так как количество продукции не может быть отрицательным числом, то переменные x 1, x 2 , x 3 принимают только неотрицательные значения:
| x 1³0, x 2 ³0, x 3³0 | (4.3) |
Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений системы неравенств (4.2) требуется найти такое, при котором функция (4.1) принимает максимальное значение.
Рассмотренная задача относится к задачам линейного программирования и является задачей распределительного типа, суть которых заключается в следующем. Пусть рассматриваемая система характеризуется наличием п видов производственной деятельности, для осуществления которых имеются различные ресурсы с номерами 
. Возможный объем потребления i -го ресурса ограничен неотрицательной величиной bi,а его расход для производства единицы продукта j- говида производственной деятельности равен aij, где 
, причем, единица продукта j- говида производственной деятельности характеризуется величиной cj,называемой удельной прибылью.Необходимо определить объемы хj, 
,производственной деятельности каждого вида, обеспечивающие максимальный суммарный доход от производственной деятельности системы в целом без нарушения ограничений, накладываемых на использование ресурсов.
|
|
|
Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции:
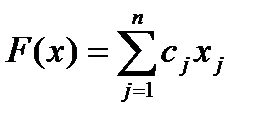→max(min) (4.4)
при ограничениях
, (4.5)
, (4.6)
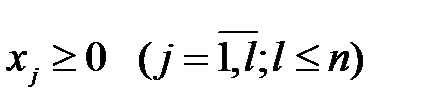, (4.7)
где aij, bi и cj – заданные постоянные числа, причем k ≤ m ≤ l ≤ n, а bi ≥ 0
При этом система линейных уравнений (4.6) и неравенств (4.5), (4.7), определяющая допустимое множество решений задачи, называется системой ограничений задачи линейного программирования, а линейная функция F (x) называется целевой функцией задачи (4.4) – (4.7) или критерием оптимальности.
Задачи линейного программирования представляют собой оптимизационные задачи из сферы планирования и управления производством. По некоторым источникам [73], 80 – 85 % всех решаемых на практике задач относятся к задачам линейного программирования.
Для решения задач линейного программирования используют симплексный метод. Процесс решения задачи линейного программирования симплекс-методом имеет итерационный характер: однотипные вычислительные процедуры в определенной последовательности повторяются до тех пор, пока не будет найдено оптимальное решение. Кроме определения оптимального решения, с помощью симплексного метода можно получить экономическую интерпретацию оптимального решения и провести анализ математической модели на чувствительность.
|
|
|
