Электростатика. Постоянный электрический ток

Закон Кулона

,

где F - сила взаимодействия точечных зарядов Q ₁ и Q ₂;

r - расстояние между зарядами;

e - диэлектрическая проницаемость;

e_o - электрическая постоянная.

Напряженность электрического поля и потенциал

, ,

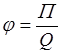где P - потенциальная энергия точечного положительного заряда Q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).

Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда

, P=j Q.

Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей)

,

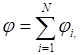
где , - напряженность и потенциал в данной точке поля, создаваемого i -м зарядом.

Напряженность и потенциал поля, создаваемого точечным зарядом

где r - расстояние от заряда Q до точки, в которой определяются напряженность и потенциал.

Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстоянии r от центра сферы:

а) E= 0, j= (при r<R);

б) E= , j= (при r=R);

в) E= , j= (при r>R),

где Q - заряд сферы.

Линейная плотность заряда

t=Q/l.

Поверхностная плотность заряда

s=Q/S.

Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью t, то на линии выделяется малый участок длиной dl с зарядом dQ=tdl. Такой заряд можно рассматривать как точечный и применять формулы

,

где - радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.

Используя принцип суперпозиции электрических полей, находим интегрированием напряженность 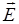и потенциал j поля, создаваемого распределенным зарядом

.

Интегрирование ведется вдоль всей длины l заряженной линии.

Напряженность поля, создаваемого бесконечной, равномерно заряженной прямой линией или бесконечно длинным цилиндром

E= ,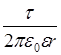

где r - расстояние от нити или оси цилиндра до точки, напряженность поля в которой определяется.

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью

E= .

Связь потенциала с напряженностью:

а) 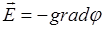, или вобщем случае ;

б) Е = ()/d в случае однородного поля;

в) в случае поля, обладающего центральной или осевой симметрией.

Электрический момент диполя

P=|Q|l,

где Q - заряд;

l - плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).

Работа сил поля по перемещению заряда Q из точки поля с потенциалом j ₁ в точку с потенциалом j ₂

A ₁₂ =Q .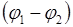

Электроемкость

C=Q/j или С=Q/U,

где j - потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю);

U - разность потенциалов пластин конденсатора.

Электроемкость плоского конденсатора

C= ,

где S - площадь пластины (одной) конденсатора;

d - расстояние между пластинами.

Электроемкость батареи конденсаторов:

a) при последовательном соединении ;

б) при параллельном соединении C= ,

где N - число конденсаторов в батарее.

Энергия заряженного конденсатора:

W=QU/ 2, W=CU²/ 2, W=Q²/ 2 C.

Сила постоянного тока

I=Q /t,

где Q- заряд, прошедший через поперечное сечение проводника, за время t.

Плотность тока

j=I/s,

где s - площадь поперечного сечения проводника.

Связь плотности тока со средней скоростью <v> направленного движения заряженных частиц

j=Qn<v>,

где Q - заряд частицы;

n - концентрация заряженных частиц.

Закон Ома:

а) для участка цепи, не содержащего ЭДС

I= ,

где 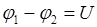- разность потенциалов (напряжение) на концах участка цепи;

R - сопротивление участка,

б)для участка цепи, содержащего ЭДС

± I= ,

где e - ЭДС источника тока;

R - полное сопротивление участка (сумма внешних и внутренних сопротивлений),

в)для замкнутой (полной) цепи

,

где R - внешнее сопротивление цепи;

R_i - внутреннее сопротивление цепи.

Законы Кирхгофа:

а) - первый закон;

б) 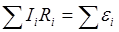- второй закон,

где - алгебраическая сумма сил токов, сходящихся в узле;

- алгебраическая сумма произведений сил токов на сопротивления участков;

- алгебраическая сумма ЭДС.

Сопротивление R и проводимость G проводника

R=pl/S, G= S/l,

где р - удельное сопротивление;

- удельная проводимость;

l - длина проводника;

S - площадь поперечного сечения проводника.

Сопротивление системы проводников:

а)при последовательном соединении R= ;

б ) при параллельном соединении ,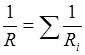

где R_i - сопротивление i -го проводника.

Работа тока:

A=IUt, A=I ² Rt, A=U ² t/R.

Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две - для участка, не содержащего ЭДС.

Мощность тока

p=IU, p=I²R, p=U²/R.

Закон Джоуля-Ленца

Q=I²Rt.

Закон Ома в дифференциальной форме

j= E,

где - удельная проводимость;

E - напряженность электрического поля;

J - плотность тока.

Связь удельной проводимости с подвижностью b заряженных частиц (ионов)

,

где Q - заряд иона; n - концентрация ионов; b_- и b ₊ - подвижности положительных и отрицательных ионов.

Электромагнетизм

Связь магнитной индукции В с напряженностью Н магнитного поля

,

где m - магнитная проницаемость изотропной среды;

m₀ - магнитная постоянная.

В вакууме m = 1, и тогда магнитная индукция в вакууме

.

Закон Био-Савара-Лапласа

или ,

где магнитная индукция поля, создаваемого элементом провода длиной dl с током I;

радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция;

угол между радиус-вектором и направлением тока в элементе провода.

Магнитная индукция в центре кругового тока

B = ,

где R - радиус кругового витка.

Магнитная индукция на оси кругового тока

B = ,

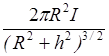где h - расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля прямого тока

B= ,

где r ₀ - расстояние от оси провода до точки, в которой определяется магнитная индукция.

В соответствии с рисунком 1, магнитная индукция поля, создаваемого отрезком провода с током (рисунок 1, а)

.

Обозначения ясны из рисунка. Направление вектора магнитной индукции обозначено крестиком – это значит, что вектор направлен перпендикулярно плоскости чертежа от нас.

При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция (рисунок 1, б)

.

Магнитная индукция поля соленоида

B=mm_onI,

где n - отношение числа витков соленоида к его длине.

Сила, действующая на провод с током в магнитном поле (закон Ампера)

, или F=IBlsina,

где l - длина провода;

a - угол между направлением тока в проводе и вектором магнитной индукции .

Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять к каждому элементу провода в отдельности

.

Магнитный момент плоского контура с током

,

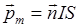где - единичный вектор нормали (положительной) к плоскости контура;

I - сила тока, протекающего по контуру;

S - площадь контура.

Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле

или ,

где a - угол между векторами и .

Потенциальная энергия (механическая) контура с током в магнитном поле

Пmех = – pmB или .

Отношение магнитного момента p_m, к механическому L (моменту импульса) заряженной частицы, движущейся по крутой орбите

,

где Q - заряд частицы;

m - масса частицы.

Сила Лоренца

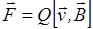или F=QvB sina,

где v - скорость заряженной частицы;

a - угол между векторами v и B.

Магнитный поток:

а) в случае однородного магнитного поля и плоской поверхности

F=B S cosa,или F=B_n S,

где S - площадь контура;

a - угол между нормалью к плоскости контура и вектором магнитной индукции.

б) в случае неоднородного поля и произвольной поверхности (интегрирование ведется по всей поверхности)

F = .

Потокосцепление (полный поток)

Y=NF.

Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

Работа по перемещению замкнутого контура в магнитном поле

A=IDF.

ЭДС индукции

.

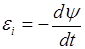Разность потенциалов на концах провода, движущегося со скоростью 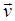в магнитном поле с индукцией

U=Blvsina,

где l - длина провода;

a - угол между векторам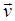и и .

Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур

Q= 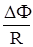, или Q= ,

где R - сопротивление контура.

Индуктивность контура

L= .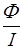

ЭДС самоиндукции

.

Индуктивность соленоида

L = ,

где n - отношение числа витков соленоида к его длине;

V - объем соленоида.

Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:

а) I = 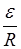(1- ) (при замыкании цепи),

где - ЭДС источника тока;

t - время, прошедшее после замыкания цепи;

б) I = I ₀ (при размыкании цепи),

где I ₀ - сила тока в цепи при t =0;

t - время, прошедшее с момента размыкания цепи.

Энергия магнитного поля

.

Объемная плотность энергии магнитного поля (отношение энергии магнитного поля соленоида к его объему)

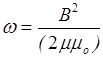или или ,

где B - магнитная индукция;

H - напряженность магнитного поля.

Оптика

Скорость света в среде

,

где c - скорость света в вакууме;

n - показатель преломления среды.

Оптическая длина пути световой волны

L=nl,

где l - геометрическая длина пути световой волны в среде с показателем преломления n.

Оптическая разность хода двух световых волн

.

Зависимость разности фаз от оптической разности хода световых волн

,

где l - длина световой волны.

Условие максимального усиления света при интерференции

…).

Условие максимального ослабления света

.

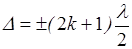Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки

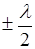, или ,

где d - толщина пленки;

n - показатель преломления пленки;

i ₁ - угол падения;

i ₂ - угол преломления света в пленке.

Радиус светлых колец Ньютона в отраженном свете

r_k = , (k =1,2,3, …),

где k - номер кольца;

R - радиус кривизны.

Радиус темных колец Ньютона в отраженном свете

r_k = .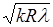

Угол j отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции на одной щели, определяется из условия

a sinj = , (k = 0,1,2,3, …),

где а - ширина щели;

k - порядковый номер максимума.

Угол j отклонения лучей, соответствующий минимуму (темная полоса), при дифракции света на дифракционной решетке определяется из условия

dsinj= l, (k = 1,2,3, …),

где d - период дифракционной решетки.

Разрешающая способность дифракционной решетки

R=l/Dl=kN,

где Dl - наименьшая разность длин волн двух соседних спектральных линий (l и l + 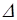l), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки;

N - полное число щелей решетки.

Формула Вульфа-Брэгга

2d sinq=kl,

где q - угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскостью в кристалле);

d - расстояние между атомными плоскостями кристалла.

Закон Брюстера

tg e_B=n ₂₁,

где e_В - угол падения, при котором отразившийся от диэлектрика луч полностью поляризован;

n ₂₁ - относительный показатель преломления второй среды относительно первой.

Закон Малюса

J=J ₀ cos ² a,

где J ₀ - интенсивность плоскополяризованного света, падающего на анализатор;

J - интенсивность этого света после анализатора;

a - угол между направлением колебаний электрического вектора света, падающего на анализатор, и плоскостью пропускания анализатора (если колебания электрического вектора падающего света совпадают с этой плоскостью, то анализатор пропускает данный свет без ослабления).

Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:

а) j=ad (в твердых телах),

где a - постоянная вращения;

d - длина пути, пройденного светом в оптически активном веществе,

б) j = d (в растворах),

где - удельное вращение;

- массовая концентрация оптически активного вещества в растворе.

Релятивистская масса

или ,

где m ₀ - масса покоя частицы;

V - ее скорость;

с - скорость света в вакууме;

b - скорость частицы, выраженная в долях скорости света (b = V / c).

Взаимосвязь массы и энергии релятивистской частицы

E=mc ² или E= = ,

где E ₀= m ₀ c ² - энергия покоя частицы.

Полная энергия свободной частицы

Е =Е ₀ +Т,

где Т - кинетическая энергия релятивистской частицы.

Кинетическая энергия релятивистской частицы

T =(m - m ₀) c ² или T = E ₀

Импульс релятивистской частицы

р = или p = m ₀ c .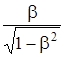

Связь между полной энергией и импульсом релятивистской частицы

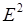= +(pc)².

Закон Стефана-Больцмана

R _e= T ⁴ s

где R _e - энергетическая светимость (излучательность) абсолютно черного тела;

s - постоянная Стефана-Больцмана;

T - термодинамическая температура Кельвина.

Закон смещения Вина

l_m=b/T,

где l_m - длина волны, на которую приходится максимум энергии излучения;

b - постоянная Вина.

Энергия фотона

,

где h - постоянная Планка;

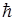- постоянная Планка, деленная на 2p;

n- частота фотона;

- циклическая частота.

Масса фотона

m=e/c ²= h /(cl),

где c - скорость света в вакууме;

l - длина волны фотона.

Импульс фотона

p=mc=h/l.

Формула Эйнштейна для фотоэффекта

h = A + T_max = A +(m V² _max)/2,

где hn - энергия фотона, падающего на поверхность металла;

А - работа выхода электрона;

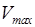- максимальная скорость вырывания фотоэлектронов;

Т _max - максимальная кинетическая энергия фотоэлектрона.

Красная граница фотоэффекта

n _o= A/h или l _o= hc/A,

где n _o - минимальная частота света, при которой еще возможен фотоэффект;

l _o - максимальная длина волны света, при которой еще возможен фотоэффект;

h - постоянная Планка;

c - скорость света в вакууме.

Формула Комптона

Dl=l´ - l = или Dl=l´ - l = ,

где l - длина волны фотона, встретившегося со свободным или слабосвязанным электроном;

l´ - длина волны фотона, рассеянного на угол q после столкновения с электроном;

m ₀ - масса покоящегося электрона.

Комптоновская длина волны

L = h /(m _o c), (L =2.436∙10^-12 м).

Давление света при нормальном падении на поверхность

p = E _o(1+ )/ c = w (1+ ),

где E _e - энергетическая освещенность (облученность);

w - объемная плотность энергии излучения;

- коэффициент отражения.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: