 |
Задача высокоэффективной элютивной хроматографии
|
|
|
|
Таким образом, математическая модель хроматографии основывается на системе уравнений, состоящей из условия материального баланса (9), кинетических уравнений внутренней (35) и внешней (34) диффузии, уравнений равновесия (23,26,30).
В подавляющем большинстве случаев в методах анализа аналитический сигнал формируется за счет концентрации аналита в подвижной фазе. При задании на входе хроматографической системы концентраций в ПФ и при определении концентраций в ПФ на выходе системы возможно такое построение математической модели, когда концентрации в неподвижной фазе становятся вспомогательными величинами и в окончательных выражениях не участвуют. Именно по этой причине хроматографическую систему иногда представляют как «черный ящик». В этой связи для удобства записи индексы фаз «1» и «2» для ПФ и НФ, соответственно, ниже будут опущены, а символ концентрации будет отвечать только концентрации в ПФ.
Граничные и начальные условия определяются следующей задачей высокоэффективной элютивной хроматографии:
· Концентрации компонентов в пробе 
, начальное распределение в ПФ внутри колонки:
; (36)
где 
- дельта-функция Дирака, равная бесконечности в нуле аргумента и нулю во всей остальной области, интеграл которой по области изменения аргумента нормирован на единицу; 
- объем пробы; 
- соответственно длина и площадь поперечного сечения колонки;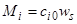 
- количество i -го компонента пробы.
· Концентрации компонентов подвижной фазы, зависимость от времени:
(изократический режим), (37)
где индексы 
- нумеруют компоненты пробы и ПФ, соответственно;
· требуется определить зависимости концентраций компонентов в ПФ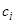 
, от времени t, и координаты x.
|
|
|
Решение системы уравнений сорбции для режима хроматографии записывается в виде:
, (38)
где 
- скорость движения фронта компонента пробы (13); 
— скорость ПФ в колонке, пересчитанная на ее полное сечение (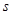
): 
, 
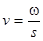— расход (скорость потока) ПФ;
(39)
— период установления равновесия с учетом всех диффузионных механизмов, который с хорошей точностью (при пренебрежении 
в сумме с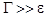 
) равен удвоенной сумме характерных времен внешней, внутренней и продольной диффузии (последняя величина равна 
). Удвоение связано с обратимостью актов сорбции в хроматографическом процессе.
Характерное время установления равновесия простым образом связано с высотой, эквивалентной теоретической тарелке, ВЭТТ:
(40)
Физический смысл соотношения (40) заключается в том, что ВЭТТ равна расстоянию в слое сорбента, которое проходит фронт компонента, движущийся со скоростью 
за период установления равновесия 
.
С большей точностью, чем ВЭТТ, положение фронта определить невозможно по следующей причине. Пусть в начальной точке «тарелки» фронт находился в первый момент времени. В тот момент, когда фронт оказался в конечной точке «тарелки», в первой точке установилось равновесие, необходимое для дальнейшего продвижения фронта из этого места. Налицо противоречие: фронт находится одновременно в начале и в конце «тарелки». Это противоречие и приводит к дискретности шкалы расстояний.
Величина ВЭТТ для заданной химической системы и компонента «i» зависит, согласно (39,40), только от параметров подвижной фазы – концентраций ее компонентов и скорости. В частности, зависимость этой величины от скорости обычно имеет вид зависимости Ван-Деемтера (рис. 3.4):
Рис. 3.4. Зависимость ВЭТТ от скорости ПФ (кривая Ван-Деемтера).
Обозначены координаты минимума функции и точка пересечения асимптот.
,
однако более точно, из (35,39,40) следует:
, (41)
где коэффициенты имеют вид, представленный в таблице 3.1.
|
|
|
Таблица 3.1. Коэффициенты уравнения (41) для вкладов кинетических стадий в ВЭТТ
| Фактор | Выражение для коэффициента |
| Продольная дисперсия | 
|
| Внешняя диффузия | 
|
| Внутренняя диффузия | 
|
Как видно из таблицы 3.1, величина ВЭТТ зависит не только от гидродинамических и кинетических параметров, но и от равновесных характеристик. В аналитической хроматографии для уменьшения времени хроматографического анализа емкость обычных сорбентов снижают в десятки и сотни раз. Как изменяется при этом ВЭТТ? Основываясь на формулах (13,26,39,40), пренебрегая величиной порозности в сравнении с коэффициентом распределения (
), при неизменных характеристиках ПФ (скорость 
, эквивалентная концентрация 
) получим:
, (42)
где 
- свободный член зависимости; n – показатель дискриминации, обычно равный 1; 
(таблица 3.2). Зависимость (42) получена для процессов конкурентной сорбции, главным образом, реализующихся в жидкостной хроматографии (ЖХ); ее вид не изменится для свободной сорбции (см. (23)), которая реализуется в газовой хроматографии (ГХ), при условии, что 
, а 
.
Таблица 3.2. Коэффициенты уравнения (42) для вкладов кинетических стадий в ВЭТТ
| Фактор | Выражение для коэффициента |
| Продольная + внешняя диффузии |
|
| Внутренняя диффузия |  (ЖХ); (ГХ)
|
График зависимости (42), построенный для переменных 
, приведен на рис. 3.5.
Рис. 3.5. Зависимость ВЭТТ от емкости разделяющего сорбента в приведенных переменных 
Из него следует, что для достаточно больших значений емкости ВЭТТ от емкости почти не зависит и имеет минимальное значение, равное 
. При уменьшении емкости ВЭТТ растет и для малой емкости становится обратно пропорциональной величине емкости с коэффициентом 
, определяемым внутренней диффузией. Подчеркнем эту особенность: кинетический режим хроматографии в колонке с малой емкостью является внутридиффузионным.
Формула (38) при 
описывает участок выходной кривой хроматографического эксперимента, относящийся к данному компоненту. Сложив их с весами, определяемыми селективностью детектирования, т.е. разной чувствительностью детектора по отношению к различным компонентам, получим
. (43)
где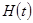 
— величина сигнала детектора в момент 
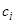; — концентрация компонента пробы в ПФ на выходе из разделяющей колонки; 
— коэффициент чувствительности детектора к данному компоненту. Из уравнения (43) видно, что высота пика какого-либо аналита складывается из основной части, пропорциональной его количеству, введенному в хроматограф, чувствительности к нему детектора и обратно пропорциональной расходу ПФ и полуширине пика, и «хвостов» других пиков, которые, однако, экспоненциально (т.е. быстро — за несколько собственных полуширин) затухают.
|
|
|
Лекция 4 (2 часа)
|
|
|
