Классическая детерминистическая модель управления запасами

 

Рассмотрим одну из классических и наиболее распространенных на практике оптимизационных моделей управления запасами. Эта модель предполагает следующие допущения:

- спрос (расход) является детерминированным и постоянным

(a(t)=a=const);

- период между двумя смежными заказами (поставками) постоянен

();

- спрос удовлетворяется полностью и мгновенно ();

- страховой запас отсутствует;

- емкость склада не ограничена;

- затраты на выполнение заказа (с₀) и цена поставляемой продукции в течение планового периода постоянные;

- затраты на хранение единицы запаса в течение года постоянные и равны c_h.

Критерием оптимизации размера заказа на пополнение запасов в данной модели является минимум общих затрат на выполнение заказов и хранение запаса на складе в течение планового периода, например, года.

Определим суммарные затраты в модели управления запасами . Предположим, что годовая потребность в материальных ресурсах равна D, а объем партии поставки q. Тогда за год необходимо сделать D/q поставок на пополнение запаса, а годовые затраты на выполнение заказов будут равны

. (10.1)

Затраты на хранение запасов на складе в течение года можно определить по формуле

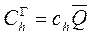, (10.2)

где - средняя величина запаса, поддерживаемая на складе.

Затраты 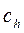могут быть выражены в долях (или процентах) от стоимости единицы продукции. Тогда

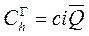, (10.3)

где с – цена единицы продукции, хранимой на складе;

i – доля от цены, приходящаяся на затраты по хранению запасов.

Средняя величина запаса будет равна q/2.

Тогда для суммарных годовых затрат получим

, (10.4)

Оптимальный размер заказа q* будет соответствовать минимуму суммарных затрат в точке, где .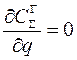

Возьмем производную выражения (10.4) и приравняем ее нулю:

(10.5)

Решая уравнение (10.5) относительно q, получим:

. (10.6)

В оригинале формула для оптимального размера заказа была получена Ф.У. Харрисом в 1913 г., однако в теории управления запасами она больше известна как формула Уилсона.

Оптимальное количество заказов за год N* и интервал времени между двумя смежными заказами 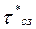будут соответственно равны:

 

; (10.7)

(дней). (10.8)

 

Рассмотрим пример 1.

Исходные данные для расчета приведены в таблице

Параметры	D, штук	c0, руб	i, %	c, руб
Величина		60,8	22,0	29,3

 

Для определения q* используем формулу (10.6)

 

.

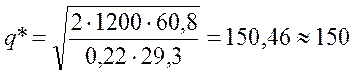Таким образом, оптимальная величина заказа (партии поставки) будет равна 150 единиц продукции.

По формуле (10.7) определим оптимальное количество заказов за год

заказов.

Оптимальное время между двумя смежными заказами будет равно

дней.

 

Задание 5

Задача 1.

Ежедневный спрос на некоторый продукт составляет 100 ед. Затраты на приобретение каждой партии этого продукта, не зависимые от объема партии, равны 100 $, а затраты на хранение продукта – 0,02 $ в сутки. Определить оптимальный объем партии и интервал между поставками.

Задача 2.

Потребность сборочного предприятия в деталях некоторого типа составляет D деталей в год, причем эти детали расходуются в процессе производства равномерно и непрерывно. Детали поставляются партиями равного объема. Хранение детали на складе стоит c_h руб в сутки, а поставка партии c₀.

 

Хар-ка	Номер варианта
D
c0
ch	0,35	0,4	0,42	0,37	0,41	0,38	0,33	0,34	0,36	0,39

Определить наиболее экономичный объем партии и интервал между поставками.

Задача 3.

По условиям предыдущей задачи определить, на сколько процентов увеличатся затраты на создание и хранение запаса по сравнению с минимальными затратами при объеме заказываемых партий – 1000 деталей.

 

Важную роль в теории управления запасами для моделей с 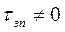играет определение момента заказа (t_з) или такого уровня (Q_з), когда необходимо делать заказ.

Точка заказа может быть определена с использованием параметра величины спроса (a) по формуле

. (10.9)

Если в условиях предыдущего примера предположить, что дней, и, учитывая, что a=D/365, получим

ед.

Таким образом, мы должны подавать заказ на пополнение запаса, когда уровень запаса на складе снизится до 33 единиц товара.

В тех случаях, когда время транспортировки заказа на склад занимает большую часть времени его выполнения и сопоставимо с циклом пополнения запаса , необходимо учитывать затраты, связанные с обслуживанием запаса в пути.

Классическая модель не учитывает эти затраты. Рассмотрим модернизированную модель, учитывающую затраты на запасы в пути с целью возможного выбора способа доставки из нескольких видов транспорта.

Введем следующие обозначения:

с _п – затраты, связанные с запасом в пути на единицу продукции в год;

- время в пути;

- средняя величина запаса в пути.

Среднюю величину запаса в пути можно определить по формуле

. (10.10)

С учетом приведенных выше обозначений и формулы (10.10) суммарные затраты будут равны

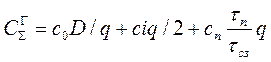. (10.11)

Если по аналогии с затратами c_h представить затраты c_п в долях (j) от цены единицы товара, то формула (10.11) примет вид

 

. (10.12)

Рассмотрим пример 2.

Пусть в условиях примера 1 у фирмы есть возможность выбора доставки заказа на склад железной дорогой или автомобильным транспортом при следующих исходных данных:

- время доставки заказа по железной дороге равно 10 дней, а автомобильным транспортом – 7 дней:

- тарифы за единицу груза равны: железной дорогой – 0,6 д.е., автомобильным транспортом – 0,9 д.е.

Предположим, что затраты c_t составляют j=10% от цены товара. Рассчитаем затраты по двум вариантам транспортировки по формуле (10.12):

- железной дорогой

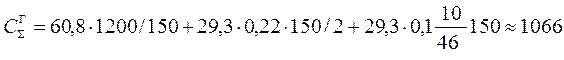д.е.

- автомобильным транспортом

д.е.

Рассчитаем общие годовые затраты, связанные с управлением запасами, с учетом затрат на транспортировку

 

- железной дорогой

д.е.

- автомобильным транспортом

д.е.

Таким образом, по критерию суммарных затрат более выгодным оказался вариант транспортировки продукции на склад по железной дороге.

Рассмотрим теперь влияние неопределенности параметров на принимаемые решения по управлению запасами.

Классическая модель является идеализированной схемой, иллюстрирующей процесс управления запасами при полностью детерминированных параметрах. На практике постоянно приходится сталкиваться с различными ситуациями, вызывающими неопределенность параметров спроса, заказа и поставок. Эта неопределенность объясняется как самой стохастической природой некоторых параметров, например, величины спроса a, так и влиянием различных рисков.

Если предположить, что параметры управления запасами Q_з, q_п, t_сз были определены для классической модели при средней интенсивности спроса , а реальный спрос является случайной величиной, распределенной по нормальному закону с дисперсией s²(a), то плотность распределения вероятностей величины Q_з будет иметь вид, представленный на рис. 4.

 

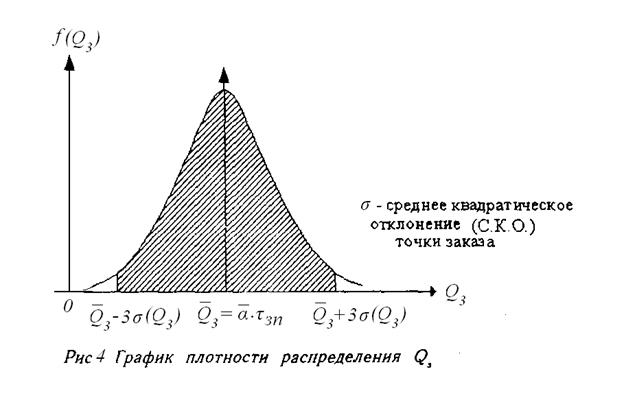
На графике показано, что разброс возможных значений Q_з вокруг среднего для нормального закона распределения с вероятностью Р=0,997 укладывается в диапазон () по правилу «трех сигм».

 

При этом

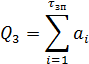
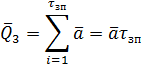
а дисперсия и среднее квадратическое отклонение Q_з составят

Неопределенность исходных параметров систем управления запасами вызывается также многочисленными рисками, например, в сроках доставки продукции, объемах поставок, качестве, ассортименте; рисками, связанными со стихийными бедствиями, возможностью хищений, пожаров, естественной убыли и т. п. Связанная с этими причинами неопределенность также может вызвать явление дефицита, причем неопределенными (стохастическими) могут быть все параметры модели управления запасами или их отдельные комбинации.

Для исключения возможности возникновения дефицита создаются страховые запасы. Определение величины страхового запаса Q _стр производится обычно на основе методов математической статистики. Для рассматриваемой модели величина точки заказа будет равна

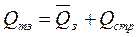. (10.14)

Наиболее простой способ расчета страхового запаса заключается в расчете доверительного интервала для Q_з по формуле

, (10.15)

где - табличное значение функции Лапласа;

- среднее квадратическое отклонение точки заказа.

Параметр определяется по величине доверительной вероятности , где - уровень значимости.

Пример. В условиях примера 1 рассчитаем страховой запас при следующих дополнительных исходных данных:

; .

По таблицам функции Лапласа находим, что =1,65. Подставляя найденное значение в формулу (10.15), получим

ед.

Точка заказа будет соответственно равна

ед.

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: