 |
Задачи транспортной логистики
|
|
|
|
Управление материальным потоком в процессе транспортировки и организация транспортирования грузов являются сферой транспортной логистики.
Транспортная логистика решает следующие задачи:
- создание транспортных систем;
- обеспечение технологического единства транспортно-складского процесса;
- выбор способа транспортировки и транспортного средства;
- определение оптимальных маршрутов доставки.
Выбор транспортного средства
Основой выбора вида транспорта, оптимального для конкретной перевозки, служит информация о характерных особенностях различных видов транспорта.
Существуют следующие виды транспорта:
- железнодорожный;
- морской;
- внутренний водный (речной);
- автомобильный;
- воздушный;
- трубопроводный.
Выделяют 6 факторов, влияющих на выбор вида транспорта: время доставки, частота отправлений груза, надежность соблюдения графика доставки, способность перевозить разные грузы, способность доставить груз в любую точку территории, стоимость перевозки.
Экспертная оценка значимости этих факторов показывает, что при выборе транспортного средства в первую очередь принимают во внимание:
- надежность соблюдения графика доставки;
- время доставки;
- стоимость перевозки.
Ранговая оценка различных видов транспорта по этим критериям приведена в табл. 6.
Т а б л и ц а 6. Ранговые оценки видов транспорта
| Вид транспорта | Надежность | Скорость | Стоимость |
| железнодорожный | |||
| автомобильный | |||
| водный | |||
| воздушный |
Составление оптимальных маятниковых маршрутов
Схема маятникового маршрута с указанием расстояний (в км) приведена на рис.8.
|
|
|
 |
6 13 7,5
 |  |
8 15
 |
Рис. 8. Схема маятникового маршрута
Здесь Г – автохозяйство;
А – склад продукции;
Б1, Б2 – потребители продукции.
Предположим, что в каждый из пунктов Б1 и Б2 необходимо совершить 2 поездки, чтобы доставить грузы со склада А.
При выполнении маятниковых маршрутов с обратным пробегом без груза возникает несколько вариантов движения автомобилей:
1) Продукция поставляется в Б2, а затем в Б1 и из Б1 автомобиль возвращается в автохозяйство Г.
2) Продукция поставляется в Б1, а затем в Б2 и из Б2 автомобиль возвращается в автохозяйство Г.
В любом варианте автомобилю придется совершить по 2 поездки с грузом как в пункт Б1, так и в пункт Б2, т. е. проехать с грузом 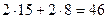 км.
км.
Также в любом варианте автомобилю придется ехать из Г в А (13 км).
Поэтому необходимо разработать такой маршрут, при котором порожний пробег был бы минимальным.
В варианте 1 нам придется проехать из Б1 в пункт Г (расстояние l(Б1;Г)), однако не надо 2-ой раз возвращаться в А (расстояние l(А;Б1)).
В варианте 2 нам придется проехать из Б2 в пункт Г (расстояние l(Б2;Г)), однако не надо 2-ой раз возвращаться в А (расстояние l(А;Б2)).
В общем случае при нескольких пунктах Бj (j=1,…,n), заканчивая работу в пункте Бj мы вынуждены дополнительно проехать расстояние l(Бj;Г), но сокращаем расстояние l(А;Бj).
Поэтому наилучшее решение получается при такой системе маршрутов, когда автомобиль заканчивает работу в пункте Бj, для которого величина l(Бj;Г) - l(А;Бj) минимальна.
Для решения задачи удобно исходные данные записать в таблицу
| Последний пункт назначения | l(Бj;Г) | l(А;Бj) | l(Бj;Г) - l(А;Бj) |
| Б1 | |||
| Б2 | |||
| ……… | |||
| Бn |
Рассмотрим применение предложенного алгоритма на конкретном примере, приведенном на рис. 8.
| Последний пункт назначения (Бj) | l(Бj;Г) | l(А;Бj) | l(Бj;Г) - l(А;Бj) |
| Б1 | -2 | ||
| Б2 | 7,5 | -7,5 |
|
|
|
Минимальное значение l(Бj;Г) - l(А;Бj) имеет место для пункта Б2 (-7,5), который принимается конечным пунктом составляемых маршрутов.
Задание 8.
Составить оптимальный маятниковый маршрут (найти конечный пункт) по данным таблицы по вариантам
| Расстояние | Номер варианта | |||||||||
| км | ||||||||||
| АБ1 | 12,5 | 8,5 | 9,5 | 10,5 | ||||||
| АБ2 | 7,5 | 3,5 | 8,5 | 7,5 | ||||||
| АГ | 9,5 | 13,5 | ||||||||
| Б1Г | 7,5 | 3,5 | 3,5 | 5,5 | ||||||
| Б2Г | 4,5 | 2,5 | 5,5 |
|
|
|


