Составление оптимальных маршрутов (транспортная задача)

 

Рассмотрим классическую транспортную задачу – задачу распределения грузов, имеющихся у поставщиков, между потребителями с целью минимизации суммарных транспортных издержек.

Пусть имеется m поставщиков и n потребителей некоторой продукции. Известны имеющиеся количества груза у поставщиков a_i>0 (i=1,…,m), потребности потребителей b_j>0 (j=1,…,n) и стоимости перевозки единицы продукта от каждого поставщика каждому потребителю – c_ij (i=1,…,m; j=1,…,n).

Требуется найти план перевозок, т. е. указать сколько единиц продукции каждый поставщик должен доставить каждому потребителю, чтобы суммарная стоимость перевозок была минимальной.

Если суммарное количество груза у поставщиков равно суммарной потребности потребителей, т. е.

,

то транспортная задача называется закрытой, в противном случае – открытой.

Условия транспортной задачи можно представить в виде таблицы

 

	b1	b2	…	bn
a1	c11	c12	…	c1n
a2	c21	c22	…	c2n
…	…	…	…	…
am	cm1	cm2	…	cmn

 

Пусть x_ij – количество единиц продукции, перевозимое от i- го поставщика j - му потребителю. План перевозок можно представить в виде матрицы

 

x₁₁ x₁₂ …… x_1n

x₂₁ x₂₂ …… x_2n

_{X = …………………………….}

x_m1 x_m2 …… x_mn

 

Условия задачи имеют вид

(i=1,…,m) (17.1)

 

(j=1,…,n)

 

(i=1,…,m; j=1,..,n) (17.2)

 

(17.3)

Задача (17.1 – 17.3) называется транспортной задачей. Для ее решения используется метод потенциалов.

Критерий оптимальности плана перевозок заключается в следующем: для того, чтобы план перевозок Х* был оптимальным, необходимо и достаточно, чтобы существовали числа: u₁, u₂, …,u_m – потенциалы поставщиков, v₁, v₂, ….,v_n – потенциалы потребителей, удовлетворяющие двум условиям:

1) (i=1,…,m; j=1,…,n)

2) если x_ij >0, то

Алгоритм метода потенциалов заключается в следующем:

- построение исходного плана перевозок методом «северо-западного» угла;

- проверка построенного плана на оптимальность при помощи критерия;

- улучшение плана, т. е. построение нового плана с меньшей стоимостью перевозок.

Алгоритм метода потенциалов применяется к закрытой транспортной задаче. Любую открытую задачу можно преобразовать в закрытую путем введения фиктивного поставщика или фиктивного потребителя.

Рассмотрим следующий пример. Пусть имеется 3 поставщика и 3 потребителя некоторой продукции. Мощности поставщиков, потребности потребителей и стоимости перевозки единицы продукции от каждого поставщика каждому потребителю заданы в таблице

 

ai / bj

Требуется найти такой план перевозок, при котором суммарная стоимость будет минимальной.

Прежде всего, подсчитаем суммарную мощность поставщиков и суммарную потребность потребителей

Так как , то задача является открытой и для сведения ее к закрытой введем фиктивного потребителя с потребностью

Стоимости перевозки единицы продукции от каждого поставщика фиктивному потребителю положим равными нулю. В результате получим закрытую транспортную задачу, условия которой содержатся в таблице

 

 

Решим полученную закрытую транспортную задачу методом потенциалов.

Составим исходный план перевозок Х₁ методом «северо-западного угла», распределяя мощности поставщиков по порядку между потребителями так, чтобы каждая перевозка была максимально возможной. У 1-го поставщика имеется 25 единиц продукции, а первому потребителю нужно 20 единиц, следовательно, ему нужно направить 20 единиц, т. е. х₁₁ =20. Оставшиеся у первого поставщика 5 единиц направим второму потребителю, т. е. положим х₁₂ =5. Недостающие второму потребителю 5 единиц продукции направим ему от второго поставщика, т. е. х₂₂ =5. Аналогично положим х₂₃ =10, х₃₃ =20, х₃₄ =15. Остальные перевозки равны нулю.

План перевозок оформим в виде таблицы, разделенной на клетки. В каждой клетке поместим перевозки х_ij. В клетки, соответствующие нулевым перевозкам, нули не вписываем, оставляя их пустыми. В таком случае план перевозок Х₁ будет иметь вид

Х₁ =

 

При описанном выше способе распределения продукции план Х₁ будет содержать не более, чем m+n-1 положительных перевозок или занятых клеток, где m - число поставщиков, n - число потребителей продукции. Остальные компоненты плана Х₁, соответствующие нулевым перевозкам, будем называть свободными клетками. Если число занятых клеток k=m+n-1, то план перевозок называется невырожденным, если k<m+n-1, то вырожденным.

Для плана Х₁ имеем k=6, m+n-1=6, следовательно план Х₁ является невырожденным.

Заметим, что если план перевозок является вырожденным, то следует часть свободных клеток считать занятыми, записав в них нули, так, чтобы общее число занятых клеток было равно m+n-1. В дальнейшем с этими нулями следует обращаться как с положительными перевозками.

Подсчитаем суммарную стоимость перевозок по плану Х₁:

.

Проверим план Х₁ на оптимальность Найдем потенциалы u₁, u₂, …,u_m поставщиков и потенциалы v₁, v₂, ….,v_n потребителей.

По условию 2 для занятых клеток

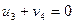, , , , , . (17.4)

Один из потенциалов всегда задается произвольно, например, зададим . Тогда из системы (17.4) получим , , , , , .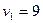

По условию 1 для свободных клеток

, , , , , . (17.5)

Подставив потенциалы, найденные из уравнений (17.4) в неравенства (17.5), получим

, , , , , .

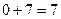Мы видим, что не выполняются два неравенства

,

.

Следовательно, план Х₁ можно улучшить, введя в план перевозку 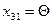, для которой разность оказалась меньше разности . С этой целью составим так называемый цикл, имеющий начало в свободной клетке (3,1), а остальные вершины – в занятых клетках, последовательно увеличивая и уменьшая перевозки, попавшие в цикл, на величину . В результате получим план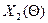

 

 

=

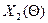20-	5+
	5-	10+
+		20-

 

Важно отметить, что при составлении цикла следует двигаться только по горизонтали или вертикали, так, чтобы в каждую строку и каждый столбец плана перевозок, охваченных циклом, попали только две перевозки.

Выберем , то есть в качестве выбирается наименьшая из перевозок, из которых вычитается. При включении в план Х₁ перевозки =5, суммарная стоимость перевозок изменится на

, то есть уменьшится на 20 единиц и для нового плана Х₂ составит

.

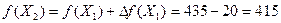Пересчитав перевозки, вошедшие в цикл плана 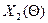при =5, получим новый план перевозок Х₂.

Х₂ =

План Х₂ лучше плана Х₁ , так как стоимость перевозки по плану Х₂ оказалась меньше стоимости перевозок по плану Х₁.

Проверим на оптимальность план Х₂. Для этого составим систему уравнений для занятых клеток плана Х₂

, , , , , .

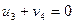Из этой системы при получим: , , , , , .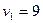

Проверим выполнение неравенств для свободных клеток плана Х₂.

, , ,

, , .

Не выполняются два неравенства, причем , . Следовательно, план Х₂ можно улучшить, введя в план перевозку . Составив цикл для свободной клетки (1,3), получим план . Выбрав , получим

,

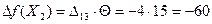и стоимость перевозок для нового плана Х₃ составит

.

=

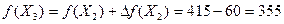15-		+
5+		15-

 

При план преобразуется в новый план Х₃. Так как совпадает с двумя перевозками, а только одна из занятых клеток должна перейти в число свободных, то в клетку (3,3) записываем 0 и считаем ее занятой.

Х₃ =

 

Для занятых клеток плана Х₃:

, , , , , .

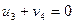Из этой системы при получим: , , , , , .

Для свободных клеток плана Х₃:

, , ,

, , .

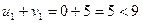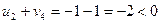Таким образом, выполняются оба условия (1 и 2) оптимальности плана перевозок. Следовательно, план перевозок Х₃ является оптимальным планом закрытой задачи, а представляет собой наименьшую стоимость перевозок. Отбросив последний столбец плана Х₃, получим оптимальный план Х* исходной открытой задачи. Отброшенный столбец означает, что первые два поставщика вывезут всю имеющуюся у них продукцию, а у третьего поставщика останутся не вывезенными 15 единиц продукции.

 

Задание 9.

Решить транспортную задачу. Заданы мощности поставщиков a_i (i=1,…,m), потребности потребителей b_j (j=1,…,n) и стоимости перевозки единицы продукта от каждого поставщика каждому потребителю – c_ij (i=1,…,m; j=1,…,n). Требуется найти план перевозок, при котором суммарные транспортные затраты будут наименьшими по вариантам:

 

 

1 вариант.

 

 

2 вариант.

 

3 вариант.

 

4 вариант.

 

5 вариант.

 

6 вариант.

 

 

7 вариант.

 

8 вариант.

 

9 вариант.

 

10 вариант.

 

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Чеботаев А.А. Логистика и маркетинг: Маркетологистика. – М.: Экономика, 2005. – 246 с.

2. Модели и методы теории логистики: Учебное пособие / Под ред. В.С. Лукинского, 2-е изд. – СПб.: Питер, 2008. – 448 с.

3. Слюсарева Е. В. Логистика: учебное пособие.- Омск: изд-во ОмГТУ, 2007.- 27 с.

4. Тяпухин А. П. Логистика: учебное пособие для студентов вузов.- Оренбург: ГОУВПО «ОГИМ», 2005.- 109 с.

5. Иванов М. Ю. Логистика: учебное пособие.- М.: РИОР, 2006.- 89 с.

6. Леонтьев В. Б. Основы логистики: учебное пособие по курсу.- М.: МИЭТ, 2007.- 71 с.

 

Содержание

 

1.История возникновения и эволюция термина «Логистика»
2. Основные понятия логистики
3. Методология и научная база логистики
4. Анализ АВС
5. АнализXYZ
6. Задачи закупочной логистики
7. Методы определения потребностей
8.Оценка и выбор поставщиков
9. Задачи управления запасами
10. Классическая детерминистическая модель управления запасами
11. Стохастические модели управления запасами
12. Складская логистика
13. Оценка работы складов
14. Задачи транспортной логистики
15. Выбор транспортного средства
16. Составление оптимальных маятниковых маршрутов
17. Составление оптимальных маршрутов (транспортная задача)
БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

⇐ Предыдущая123456789

Поделиться:

Воспользуйтесь поиском по сайту: