Многомерные корреляционные связи.

В условиях сильной “ засоренности” геофизического поля мешающими факторами можно уменьшить величину среднеквадратической погрешности ε_n, переходя от парной линейной корреляционной взаимосвязи параметров к множественной.

Весьма характерная ситуация, иллюстрирующая целесообразность такого перехода при картировании кровли кристаллического фундамента, приведена в [9]. На рис.3.8. Хорошо видно, что парная корреляция гипсометрии поверхности кристаллического фундамента, как с гравитационным Δg, так и с магнитными ΔТ полями, слабая. Форма аномальной кривой Δg обусловлена на такой модели двумя факторами: моноклинальным погружением кристаллического фундамента, сложенного гранито-метаморфическими породами и гравитационным влиянием базальтовых интрузий, пронизывающих его толщу. Поле ΔТ сформировано в основном магнитоактивными базальтами, в то время как вмещающие их метаморфические породы фундамента слабо намагничены и в нем не отражаются. Если теперь составить регрессионное уравнение вида

Н_ф=А₀+А₁Δg+А₂ΔТ, (3.20)

то есть включить в оператор А_φ разные парные корреляционные связи – сделать его многомерным, - прогноз Н_ф будет более эффективным. Иными словами, многомерная связь должна быть теснее, чем парная, а ошибка приближения ε_п(Н/Δg, ΔТ) – меньше, чем ε_п(Н/Δg) или ε_п(Н/ΔТ).

В приведенном примере составление и использование многомерного оператора равносильно исключению влияния базальтовых тел, зафиксированного в рельефе кривой ΔТ, из поля Δg. В результате кривая Δg как бы исправится, то есть ее связь с гипсометрией фундамента станет более тесной.

 

Приемы вычисления коэффициентов многомерной регрессии ничем не отличаются от парного случая.

Образовав в точках эталонного пространства (Н,Δg,ΔТ)_φ разности

А₀+А₁Δg_i+А₂ΔТ_i - Н_i = ΔН_i,

минимизируют сумму их квадратов:

(3.21)

Дифференцируя формулу (21) по А₀,А₁ и А₂ с учетом линейности оператора суммирования, переходят к системе нормальных уравнений:

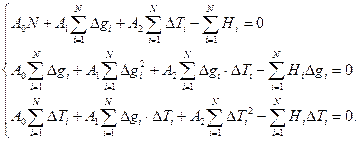(3.22)

 

Решая ее относительно коэффициентов регрессионного оператора А₀,А₁ и А₂ получают

 

(3.25)

(3.23)

(3.24)

Оценкой тесноты многомерной корреляционной связи служит множественный (сводный) коэффициент корреляции [10]:

(3.26)

Он обладает теми же свойствами, что и r в случае парной регрессии. Множественный коэффициент R равен нулю, когда линейная статистическая взаимосвязь между параметрами Н,Δg и ΔТ полностью отсутствует (отметим еще раз, что это отнюдь не исключает наличия между ними какого-либо иного типа связи). Стремление R к единице соответствует переходу статистической линейной зависимости в функциональную.

Если поля Δg и ΔТ информативны в отношении Н, величина R превосходит значения коэффициентов парной корреляции. Тогда и ошибка приближения, равная для многомерного случая

(3.27)

уменьшится в сравнении с парным, а точность прогнозирования соответственно увеличится

Силу “влияния” каждого из прогнозирующих параметров на Н в многомерной связи уже нельзя измерить по величине парных коэффициентов r(Δg,H) и r(ΔT,H) – они дают лишь приближенную оценку корреляции. Более объективно охарактеризовать это “влияние”, то есть по сути дела сопоставить “информативность” прогнозирующих параметров, позволяют так называемые частные коэффициенты корреляции:

, (3.28)

 

(3.29)

 

В этих выражениях влияние третьего параметра, вынесенного за скобки в левых частях равенств, исключается и, таким образом, связь Δg или ΔТ с Н измеряется в относительно чистом виде.

Хотя за счет увеличения числа членов регрессионного уравнения ошибка приближения ε_п, посчитанная в эталонных точках, уменьшается, описать зависимость между Н и геофизическими данными с необходимой для решения прогнозной задачи точностью удается не всегда. Действительно, большое число прогнозирующих параметров приводит к излишней “индивидуализации” оператора связи А_φ, и он не выдерживает процедуры независимого контроля, то есть ошибка на контрольной выборке ε_к, вычисляемая по формуле (18), оказывается недопустимо большой. Происходит это потому, что параметр, информативный на эталоне, в прогнозной области может вести себя незакономерно, а его включение в оператор связи снижает достоверность последующего прогнозирования. Кроме того, далеко не всегда использование множественной регрессии позволяет скорректировать суммарный характер геофизических полей.

 

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: