Корреляционный метод, основанный на предварительном разделении прогнозирующего поля.

Предварительное разделение суммарных полей на составляющие, обусловленные отдельными геофизическими границами, должно конечно приводить к существенному повышению эффективности корреляционной прогнозной процедуры. Однако, классический аппарат различных трансформаций, развитый в гравиразведке и магниторазведке, не всегда эффективен, так как их параметры в пределах исследуемой территории, как правило, постоянны и выбираются на основе эмпирических критериев или исходя из априорных представлений о частотном составе разделяемых компонент поля. На практике разделение с помощью таких преобразований в большом количестве случаев неоптимально с геологических позиций. Поэтому операцию разделения целесообразно осуществлять приемами, которые позволили бы выделить из суммарного поля составляющую наиболее тесно корреляционно связанную с изучаемой характеристикой Н. Получить такую информативную в отношении Н компоненту поля позволяет корреляционный метод разделения (КОМР) геофизических аномалий [17].

Наблюденное поле (для определенности будем говорить о Δg) разделяется в КОМР на остаточную составляющую и фоновую

Δg=Δg₀+Δg_фон, (3.30)

где под фоновой компонентой поля понимается та его часть, вычитание которой из Δg приводит к максимизации коэффициента корреляции

|r(H,Δg₀)|=max (3.31)

то есть дает остаток Δg₀ лучше всего корреляционно связанный с Н.

Фоновая компонента ищется в виде многочлена заданной степени от координат эталонных точек, удовлетворяющего поставленному условию (31)

 

(3.32)

где х,у – координаты точек наблюдения; λ_pq – коэффициенты фонового многочлена; n=max(A,B) – порядок фоновой составляющей.

Коэффициенты выбираются так, чтобы они максимизировали функцию γ(λ_pq):

(3.33)

Дифференцируя (33) по λ_pq и, приравнивая производные нулю, получаем систему алгебраических уравнений для определения λ_pq. В частном случае, при выделении фона первого порядка:

Δg_фон =λ ₁₀ x+λ₀₁у (3.34)

Величины λ₁₀ и λ₀₁ определяются из соотношений [ ]

; (3.35)

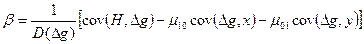
(3.36)

 

 

(3.37)

Отметим теперь, что поскольку максимально возможная величина коэффициента корреляции равна единице, условие (31) с учетом формулы (11)можно переписать так:

 

(3.38)

 

откуда

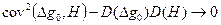(3.39)

или, имея ввиду, что

D(Δg₀)=cov(Δg₀,Δg₀) и D(H)=cov(H,H) получим (3.40)

cov²(Δg₀,H)-cov(Δg0,Δg₀)·cov(H,H)→0.

Последнее соотношение равносильно минимизации определителя матрица ковариаций

(3.41)

Так как в большинстве конкретных геолого-геофизических ситуаций (в том числе и при изучении строения поверхности фундамента) корреляционная связь представляется многофакторной зависимостью, анализу по КОМР могут подвергаться не два, а три параметра (например, кроме Н_ф и Δg, еще ΔТ). Тогда фоновая составляющая вычисляется на основе минимизации определителя такой ковариационной матрицы

 

(3.42)

Для нахождения λ_pq в [16] получено выражение

(3.43)

где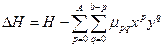

а величины определяются решением системы линейных уравнений

 

= (3.44)

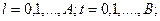
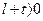
В частном случае парной связи Δg c H и фоновой составляющей (32) первого порядка, из (44) автоматически получается система (37).

Контроль оптимальности (геологической содержательности) корреляционного разделения Δg в зависимости от порядка n фоновой составляющей осуществляется в КОМР по величине оценки стандартного отклонения S(Δg₀). Критерием оптимальности служит условие минимума S(Δg₀), причем уменьшение значений должно происходить с ростом степени n фонового многочлена монотонно:

Sⁿ(Δg₀)< S^n-1(Δg₀)<…< S(Δg₀) (3.45)

Существо критерия (45) заключается в том, что он не позволяет использовать для выбора оптимального n равносильное ему в математическом смысле, но геологически не содержательное, условие (31).

В самом деле, математическая процедура корреляционного разделения в соответствии с (31) происходит так, что даже в случае отсутствия в поле Δg информации об Н, всегда будет найдена “составляющая” Δg₀ корреляция которой с Н близка к единице. Это происходит за счет “подстраивания” фоновой компоненты Δg_фон к Н. Однако, S(Δg₀) окажется больше стандарта исходного поля S(Δg) и станет очевидной геологическая несодержательность решения задачи разделения Δg.

Хорошей иллюстрацией этому служит рис.3.9. Здесь поверхность Н не является гравиактивной, поэтому в поле Δg (кривая1) поднятие в рельефе Н не отображается вовсе. Тем не менее в процедуре КОМР, контролируемой условием (31), будет найдена такая фоновая компонента Δg_фон (кривая 3), вычитание которой из наблюденного поля даст Δg₀ (кривая 2), максимально тесно коррелированное (r(Δg₀,H)=1) с Н. Тем самым из поля “извлекается” такая информация, которой в нем на самом деле нет. Хорошо видно, однако, что исходное поле Δg постоянно, следовательно S(Δg₀)=0, в то время как стандарт Δg₀ явно отличен от нуля. Таким образом, полученное решение должно быть отвергнуто как геологически необоснованное.

Наличие в КОМР строгих критериев оптимальности разделения [17] является одним из существенных преимуществ этого метода перед другими способами трансформации геофизических аномалий. Еще одно его важное преимущество состоит в том, что в результате корреляционного преобразования вычисляются все статистические оценки (корреляции, дисперсии и т.п.), необходимые для прогнозирования.

Когда Δg₀ выделена из суммарного поля с максимальным удовлетворением требования (33), ее связь с Н должна быть гораздо ближе к линейной, чем связь Н с исходным полем Δg.

Следовательно, можно построить линейный прогнозный оператор:

(3.46)

который дает наименьшую ошибку приближения в точках эталонного пространства :

Для точек контрольной выборки ошибку приближения удобно считать по следующей формуле:

 

 

(3.47)

где N- объем контрольной выборки; H_j- прогнозное значение, найденное в j-й точке по (46); H_jk - точное значение H в j-точке.

 

Если полученный оператор выдерживает процедуру независимого контроля, то есть 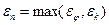не превосходит по крайней мере половины требуемого сечения прогнозных построений Δ, то можно, используя оператор (46) определить глубину залегания искомой границы Н во всех точках прогнозного пространства .

Во второй части настоящего пособия студенту будет предложена лабораторная работа, последовательно реализующая все этапы решения задачи создания с помощью корреляционной методики прогнозной структурной основы для развертывания дальнейших поисково-разведочных работ, начиная с отработки геофизических профилей и заканчивая бурением.

В уже изложенной теоретической части были представлены тексты, касающиеся, с одной стороны общей методологии комплексного применения геофизических методов: комплексной интерпретации полученных данных, а с другой стороны приведены достаточно простые, по нашему мнению, и порой избыточные примеры, иллюстрирующие некоторые положения, затронутые при обсуждении методологической проблематики. Эти примеры могут быть опущены при работе с пособием, если затрудняют уяснение теоретического аспекта курса и, напротив, востребованы при выполнении практических работ.

Литература к главе 3.

1. Бродовой В.В. Иерархический ряд физико-геологических моделей нефтегазовых объектов в свете системного подхода (Изв. Вузов “Геология и разведка”,1995г №2,с 129-135.

2.Вентцель Е.С. Теория вероятностей. М., Наука1964. 576с.

3.Яскевич В.И. Методология геологической интерпретации комплексных геофизических данных: сущность и пути развития. Москва. ВИНИГИ,1986, р.7687-В 86. 27с.

4.Пойзнер Б.Н., Ситникова Д.Л. Самообновление культуры и синтез научных знаний – Томск: изд-во Томского университета, 2002г. 184с.

5.Балк П.И. Столкновение геофизических и математических интересов – источник противоречий в современной теории интерпретации потенциальных полей. / В кню Геофизика и математика /Под. Ред. В.Н. Страхова.-М.ОИФЗ РАН,1999.с.9-12.

6.Вахромеев Г.С., Давыденко А.Ю. Моделирование в разведочной геофизике. М. Недра,1987г. 192с.

7. Комплексирование методов разведочной геофизики. Справочник геофизика / Под. Ред. В.В. Бродового, Л.Л. Никитина. М. Недра,1984г. 384с. (с.114)

8.Смилевец Н.П. Новый подход к комплексной интепретации геофизических данных. Геофизика,1997г., №6.

9.Рыскин М.И., Пимштейн И.Г. Анализ геолого-геофизической информации на мини-ЭВМ с применением корреляционных методов. Практикум по курсу «Геологическая интерпретация геофизических данных». Саратов. Изд-во СГУ,1987г.,63с.

10.Пимштейн И.Г., Рыскин М.И. Анализ геолого-геофизической информации на мини-ЭВМ с применением статистических методов. Саратов. Изд-во Саратовского госуниверситета,1986г.,42с.

11.Рыскин М.И., Лепилин В.М., Романов В.В. Разработка и опробование методики комплексного параметра (КП) при совместной интерпретации геолого-геофизических данных (предварительные итоги) – Ученые записки геологического факультета СГУ. Новая серия. Саратов. Изд-во Саратовского университета,1997. вып.1.

12. Выявление пространственных закономерностей размещения нефтегазоперспективных зон на основе структурно-геофизического районирования / Рыскин М.И., Лепилин В.М., Романов В.В.. недра Поволжья и Прикаспия. Вып.18.,1995г.

13.Гафаров Р.А. Сравнительная тектоника фундамента и типы магнитных полей древних платформ. М.Наука.1976г.

14.Никитин А.А. Комплексная интерпретация геофизических полей при изучении глубинного строения Земли / Геофизика №4,1997г.

15.Никитин А.А., Конценебин Ю.П. Современные компьютерные технологии комплексной интепретации геолого-геофизических данных. / Геолого-геофизические исследования Юго-Востока Русской плиты. Саратов, изд-во ЕАГО,2004г.

16. Комплексирование геофизических методов при поисках органогенных построек в подсолевом разрезе Прикаспийской впадины / Рыскин М.И., Романов В.В., Лепилин В.М., Кравченко Л.С. геология нефти и газа №7,1992г.

17.Шрайбман В.И., Жданов М.С., Витвицкий О.В. Корреляционный метод преобразования и интерпретации геофизических аномалий.

18.Дэвис Д. Статистика и анализ геологических данных. М., Мир,1977г.

 

 

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: