Построение изолиний поверхности топографического порядка.

Способ построения, изолиний или горизонталей поверхностей топографического порядка, интерпретирую­щих свойства исследуемых показателей' (признаков), не­сколько отличен от способа построения изогипс земной поверхности.

На чертеж наносят по координатам точки, в кото­рых определены (замерены) значения показателя (при­знака).

Около каждой точки выписывают значение показате­ля (признака). На рис. 52 нанесены устья вертикальных скважин с указанием отметок почвы угольного пласта.

Рис. 52. Построение инвариант­ных линий поверхности, задан­ной точками с числовыми отметками

 

На основе анализа отметок намечают ориентировочное положение инвариантных линий^- изображаемой по­верхности (линии тальвегов и водоразделов). Последние дают возможность наметить линии скатов изобра­жаемой поверхности и такие направления между вы­работками, изменение значений отметок по которым происходит по закону, близкому к прямой. На этих направлениях линейным интерполированием находят ступенчатые отметки изображаемой поверхности, опре­деляющие сечение ее горизонталей. Через ступенчатые отметки проводят изогипсы поверхности почвы пласта (рис. 53).

При невозможности определения инвариантных линий и направлений скатов изображаемой поверхности построение горизонталей производят методом многогранникоа. Для этого выбирают группу точек с расчетом, что­бы они образовали вершины треугольников (рис. 54). Стороны треугольников по возможности должны быть направлены по однообразным скатам, а поверхности их должны быть близкими к плоскостям.

 

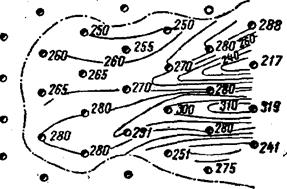Рис. 53

Рис.54 Построение горизонталей поверхности способом вписанного многоугольника

Построив горизонтали по первой группе точек, про­должают их построение с учетом других точек.

Преобразование изобра­ жений.

К преобразованию изображений в проекциях с числовыми отметками при­бегают при решении многих задач, связанных с опреде­лением по плану истинных угловых и линейных ве­личин по изображенным элементам.

Перемена плоскости про­екции.

Выбирают вспомога­тельную плоскость, перпен­дикулярную основной плос­кости проекции, и совмеща­ют ее с последней либо с плоскостью, ей параллельной, путем вращения вокруг ее следа или вокруг какой-либо горизонтали.

Пример. Требуется наметить буровую скважину из точки а 12₈ перпендикулярно плоскости кровли залежи, найти точку встречи скважины с залежью и определить наклонную длину скважины (рис. 55).

Рис. 55. Построение перпенди­куляра из данной точки на плоскость, заданную горизон­талями

 

Решение. Через точку a₁₂₈ проводят линию пер­пендикулярно горизонталям плоскости, изображающую вспомогательную плоскость профиля. Последнюю, вращая вокруг ее семидесятой горизонтали, совмещают с горизонтальной плоскостью, имеющей отметку 70.

Строят совмещенное положение прямой пересечения плоскости профиля с данной плоскостью. Для этого на перпендикулярах к проекции плоскости профиля в точ­ках K₇₀, K₁₀₀ откладывают в масштабе рисунка соответ­ственно 0 и 30 м и через эти точки проводят искомую прямую. Аналогично строят совмещенное положение точки A₁₂₈⁷⁰ для чего от точки am по перпендикуляру к проекции плоскости профиля откладывают 58 м.

Из точки A₁₂₈⁷⁰ опускают перпендикуляр на линию

K₇₀ К₁₀₀⁷⁰ определяют расстояние A₁₂₈⁷⁰В⁷⁰₈₅ — наклонную длину скважины.

Из точки В⁷⁰₈₅ (точки встречи перпендикуляра с плос­костью) опускают перпендикуляр на проекцию плоскости профиля и получают искомую проекцию перпендикуляра a ₁₂₈b₈₅.

Совмещение плоскостей.

Под совмещением плоскостей понимают приведение данной плоскости в положение, параллельное плоскости проекции.

Совмещение может быть произведено с горизонталь­ной и с вертикальной плоскостями проекции или с плос­костями, им параллельными, при этом отдельные элемен­ты, лежащие в совмещаемой плоскости, получаются в неискаженном виде.

Пример. Требуется определить угол между прямыми линиями — осями двух наклонных выработок по их про­екциям на маркшейдерском плане (рис. 56).

 

Решение. Проекции заданных прямых пересекаются за пределами рисунка. Через произвольно взятую точ­ку с'₇ прямой a₄b₈ проводят линию с₇ d₄, параллельную заданной линии с₁₁d₈ и описанным ниже путем опреде­ляют угол между прямыми а₄ 6₈ и с’₇ d’₄ который равен искомому углу.

Через линии a₄b ₈ и с’₇ d’₄ проводят плоскость. Для этого прямые градуируют. Через точки с одинаковыми отметками проводят параллельные прямые — горизонтали наклонной плоскости, проходящей через эти прямые.

вращая треугольник a₄d’₄ с’₇ вокруг горизонтали 4, совмещают его с горизонтальной плоскостью н, имеющей отметку 4. При этом точки а₄ и d’₄ останутся на месте; с₇’ переместится в точку с⁴₇ по направлению продолже­ния перпендикуляра c’₇k₄, опущенного из точки с’₇ на го­ризонталь 4 (рис. 57). Расстояние k₄c⁴₇ = k₄c₇ равно гипотенузе прямоугольного треугольника, один катет ко­торого равен расстоянию проекции совмещаемой точки до оси вращения (K₄С’₇), а величина другого равна пре­вышению точки с над плоскостью совмещения (C’₇C₇), т. е. разности их числовых отметок.

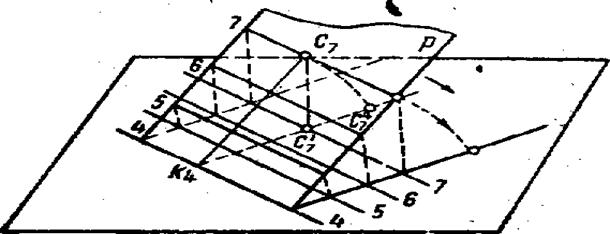Рис. 57. • Схема совмещения плоско­сти Р с горизонтальной плоскостью Н.

 

Соединяя С⁴₇ с точками а₄ и d’₄, получают совмещенное положение линий а ₄с⁴₇ и d’₄c₇ с горизонтальной плоскос­тью. н₄. Угол α между ними является искомым углом.

Пусть далее требуется определить угол между двумя плоскостями, заданными горизонталями.

Соединив точки пересечения одноименных горизонта­лей, получают линию пересечения плоскостей а₄Ь₃с₂ (рис. 58).

Через одну из точек линии пересечения плоскостей, например через точку 6а, проводят плоскость, перпендикулярную линии пересечения данных плоскостей. В ней находится линейный угол двугранного угла между плос­костями. Заложение ℓn этой плоскости определяют гра­фически, как это показано на рис. 58, или по формуле 104).

Затем находят линию пересечения этой плоскости с заданными плоскостями, для чего через точки пересе­чения одноименных горизонталей проводят прямые b_зm₂ и b_зп ₂. Точку b ₃ совмещают с горизонтальной плоско­стью Н₂ вращая ее вокруг горизонтали 2; 6₃² — сов­мещенное положение точки b₃.

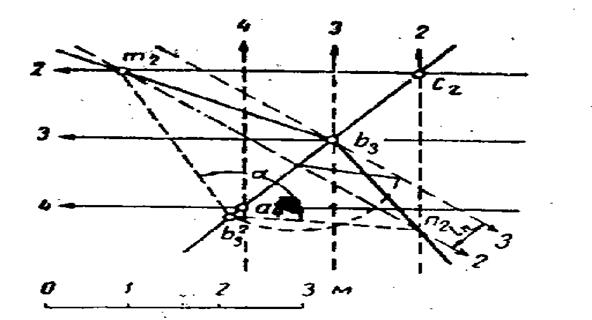
Рис. 58. Определение угла между двумя плоскостями, заданными горизонталями

 

 

 

Соединив ее прямыми линиями с точками п₂ и т₂ (пунктирные линии на рис. 58), получают искомый угол α, величину которого измеряют транспортиром.

АФФИННЫЕ ПРОЕКЦИИ

Треугольники ABC и аЬс (рис. 59) являются аф­финными (родственными) друг другу. Здесь х—х — ось родства или ось аффинного соответствия (ось

аффинитета); прямые А a, Вb, Сc параллельные между собой и определяют направление аффинитета под некоторым углом φ к оси.

При ортогональном проектировании точек плоскости направление аффинитета перпендику­лярно к оси родства.

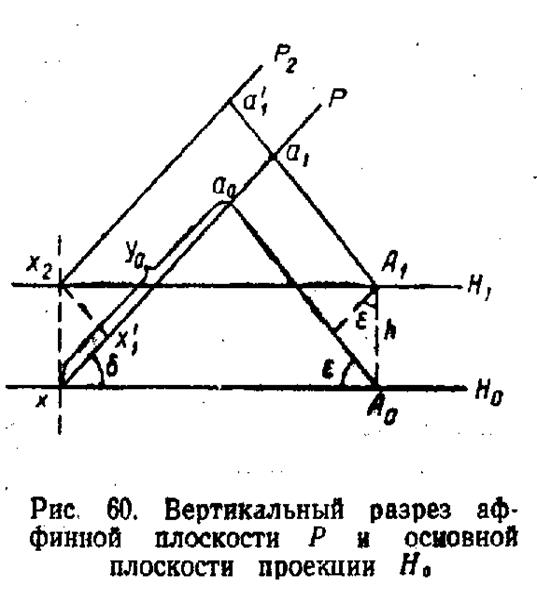
На рис. 60 изображены проекции плоскости Р и ос­новной плоскости чертежа Н₀ на плоскость, перпенди­кулярную оси родства.

Поскольку ось родства х—х горизонтальна, рис. 60 представляет собой профиль плоскостей Р и Н₀; δ — угол падения плоскости Р; є — угол наклона направ­ления проектирования к горизонтальной плоскости; а₀ — ортогональная аффинная проекция точки А₀.

По рис. 60 ордината родства точки А₀ определяется из соотношения

у₀ = хА₀ cos δ = хА₀ sin є,

где хА₀ =у' (у' — ордината точки А₀).

Формула для ординат родства (аффинная ордината) любой точки, лежащей на плоскости Н₀,

у_о=у’sin є. (105)

Проведем горизонтальное сечение Н₁ на расстоянии h от основного сечения Н₀.

Для ординат родства у₁ некоторой точки А₁ имеет место следующее соотношение:

у ₁₌ ха_г = у ₀ + а ₀ а ₁

или

у ₁₌ ха_г = у ₀ + а ₀ а ₁ (106)

 

 

Для всех точек, лежащих на плоскости H_1t второе- слагаемое формулы (106) h соз є = h sinδ остается посто­янным.

Если ось родства х — х перенести параллельно самой себе на величину

h cos є = х — х’₁. то при построении точки а ₁ можно от этой оси откладывать только одно слагаемое ее ординатыу₁, а именно у sin є.

Этот перенос оси х—х равен переносу плоскости проекции Р в положение P₂.

Точка х₂ определяет проекцию линии пересечения плоскостей P₂ и Н₁, а сама ось x₂ —-х₂ лежит в одной вертикальной плоскости с осью х — х, т. е. на плане они сливаются в одну линию.

Для построения ординат родства точек, лежащих в плоскости H₁. ось родства х₂ — x₂ переносится в поло­жение оси х’₁ — x’₁, которая называется условной осью родства данного горизонта Н₁.

При построении ординат родства точек, лежащих в плоскости H₁, достаточно определить ординаты по формуле (105) и отложить их от условной оси родствах’₁ — x’₁.

Расстояние х — х₁’ = h' условной оси родства от оси х — х определяется по формуле

h'= h sin δ = h cosє, (107)

где h — превышение данного горизонта от основной го­ризонтальной плоскости Н₀.

Аналогично находят координаты родства и для дру­гих горизонтов.

Рассмотренное ортогональное проектирование на плос­кость Р называется аффинным проектированием, а са­ма плоскость Р — плоскостью аффинных проекций.

Аффинное проектирование может быть и косоуголь­ным.

На рис. 61 приведена схема ортогонального аффин­ного проектирования горных выработок двух горизонтов

 

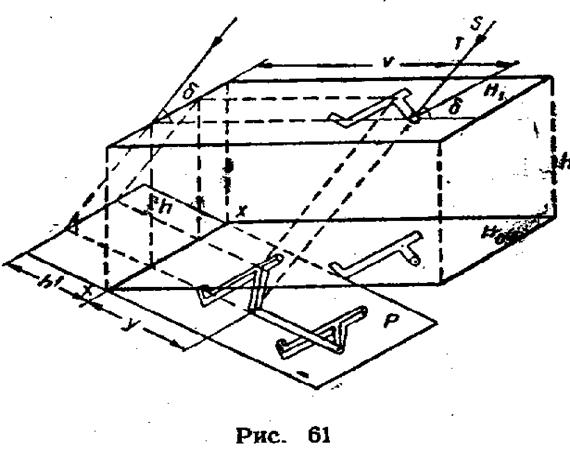
H₁ и Н₀. Направление проектирования ST перпендику­лярно плоскости Р, а с горизонтальной плоскостью Н₀ составляет угол δ.

Пример аффинного проектирования.

На рис. 62 изо­бражена в проекции с числовыми отметками усеченная

четырехгранная пирами­да. На плане выбирают ось родства — прямую ох. Опуская из вершин пирамиды на ось род­ства перпендикуляры, получают точки 1', 5', 2'. 6', 7, 3', 8’, 4'.

Для построения аф­финной проекции пира­миды (рис. 63) линию о'х' принимают за ось родства основной пло­скости плана (основания _; пирамиды) с отметкой 50.

Направление проек­тирования определяется углом є = зо°, при этом ординаты родства у₀. опре­деляемые по формуле (105), будут в два раза меньше ординат родства у' взятых с исходного плана.

На осях х — х (рис. 62) и х'—х' (рис. 63) произ­вольно устанавливают точки начала координат (о и о').

На оси х'—х' (рис. 63) отмечают абсциссы точек (принимая ось родства за, ось абсцисс), лежащих в плос­кости основания пирамиды с отметкой 50; отрезки о’—1”, о’—2", о’—3" и о’ —4" соответственно равны отрез­кам о—1', 0—2', о—3' и о— 4', полученным на рис. 62. Восстанавливая в точках 1”,3",2" и 4" перпендикуляры к оси о’х’, откладывают на них аффинные ординаты точек 1,2,3,4, т.е. отрезки 1”-1, 3-3”, 2-2”, 4-4”, соответственно равные половинам ординат этих точек, взятых с плана (рис. 62). Соединяя точки 1, 2

3 и 4, получают изображение нижней грани пирамиды. Затем на расстоянии h' в масштабе исходного плана проводят условную ось родства х"— х" горизонтальной плоскости с отметкой 70.

Перпендикуляр к оси х^г — х^г из точки 0' определит на оси х" — х" точку 0", от которой откладывают от­резки 0"—5", 0"—6", 0"—7", 0"—8", соответственно равные абсциссам 0—5', 0—7', 0—, 6', 0—8' исходного плана (рис. 62). На перпендикулярах, восставленных из точек 5", 7", 6" и 8" к оси х" — х", откладывают отрезки 5"—5, 7"— 7, 6"—6, 8" — 8, равные соответственно половинам отрезков 5'—5, 7'—7, 6'—6, 8' — 8 плана.

Полученные точки 5, 6, 7 и 8 определяют верхнее основание пирамиды с отметкой 70. Соединив соответ­ствующим образом все восемь точек прямыми, находят аффинную проекцию пирамиды.

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: