Стереографические проекции

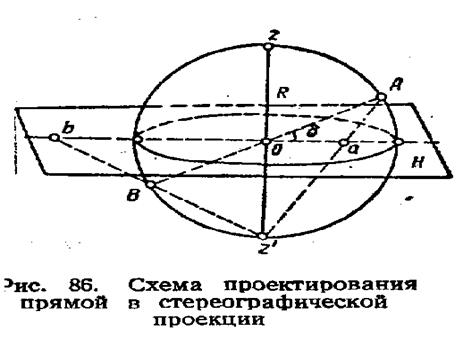
Перспективные проекции поверхности полусферы на плоскость называются стереографическими проекциями. Около некоторой точки описывают сферу радиусом R. Через центр сферы проводят горизонтальную плоскость Н, являющуюся плоскостью проекций (картинной плос­костью). Она пересекает сферу по большему кругу, на­зываемому кругом стереографических проекций. Ниж­нюю точку сферы Z' (рис. 86) принимают за точку зрения.

ПрямаяАВ, прове­денная через центр сфе­ры параллельно задан­ной прямой, проекти­руется на плоскость Н в виде ab. Чтобы опре­делить направление пря­мой в пространстве, до­статочно знать проекцию ее точки пересечения с верхней полусферой, т. к. вторая точка пря­мой находится всегда в центре сферы О,

Точка а, определяю­щая положение прямой АВ в стереографической проекции, отстоит от центра сферы на расстоянии Оа, определяемом по формуле

Оа = Rtg( 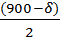), (114)

где R — радиус сферы;

δ — угол наклона прямой к плоскости Н.

Плоскость в стереографической проекции на плос­кость Я изображается дугой окружности.

 

Через центр сферы проводят прямую КМ, парал­лельную линии простирания плоскости. Через эту пря­мую проводят плоскость с углом ее падения δ; ED — линия падения. Плоскость пересечет верхнюю полусферу по дуге МЕК, проекция которой на пло­скость Н—дуга МеК (рис. 87, а).

Дуга МеК — дуга окружности, центр 0' которой от­стоит от центра 0 сферы на расстоянии 00 = Rtg δ (рис. 87, б) и делит отрезок ed пополам, т. е.

еО' = O'd - O'Z'.

Радиус этой окружности r = Rsec δ. (115)

 

 

Стереографическая проекция является равноугольной, т. к. углы между сферическими линиями, являющимися стереографическими проекциями плоскостей, равны углам между этими плоскостями. Это свойство стереографической проекции используется в маркшейдерском деле при определении углов между плоскостями и направлениями.

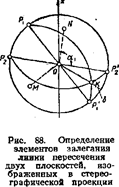
Для построения стереографических проекций плос­костей P₁ и Р₂, заданных элементами залегания (α₁, α₂ — азимутами линий простирания и δ₁, δ₂ — углами паде­ния), на круге стереографической проекции строят след Р₁Р’₁ плоскости Р₁ по дирекционному углу (азимуту) α₁, (рис. 88); проводят перпендикулярно следуР₁Р’₁ линию падения плоскости P₁, на ко­торой откладывают отрезок ОМ = R tg δ; описывают из трчки М дугу радиусом MP ₁ — стереографическую проекцию плоскости P₁.

Аналогично описанному строят стереографическую про­екцию плоскости Р₂ по ее элементам залегания (α₂, δ₂).

Для определения элементов залегания линии пересечения двух плоскостей P₁ и Р₂ про­водят линию ОК — стереогра­фическую проекцию линии пе­ресечения плоскостей и по положению точки К опреде­ляют искомые элементы зале­гания этой линии.

Угол между плоскостями P₁ и Р₂ определяется ост­рым двугранным углом MKN.

Для определения углов пользуются стереографичес­кими сетками, которые представляют собой стереогра­фическую проекцию сетки меридианов и параллелей верх­ней полусферы.

В кристаллографии широко применяется стерео­графическая сетка Вульфа.

Для маркшейдерских работ пользуются сеткой проф. В. В. Каврайского, представляющей собой изображение меридианов и

 

параллелей в поперечной равнопромежуточной азимутальной проекции (рис. 89).

Сетка Каврайского строится по точкам пересечения меридианов и параллелей через 5°. Эти точки пересече­ния наносят по полярным координатам, вычисляемым по формулам:

tgα = sin 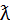\ ctg φ; (116)

 

Все построения производят на восковке, помещаемой на сетке, которую кладут на ровную поверхность стола так, чтобы северный конец диаметра SN находился вверху. На восковке карандашом намечают крестиком центр круга проекции, круг и вне круга сетки — север­ный конец диаметра сетки.

Для изображения отрезка прямой по элементам его залегания накладывают восковку на сетку, центрируют ее и начальный штрих совмещают с концом N диамет­ра сетки.

Затем от северного полюса сетки по большому кру­гу отсчитывают число градусов азимута простирания линии, отмечая отсчет штрихов вне круга. Вращая во­сковку, совмещают штрих с одним из диаметров сетки и от периферии к центру отсчитывают число градусов угла δ наклона прямой. Здесь и будет конечная точка, вектора (а). Соединив центр сетки с конечной точкой, получают отрезок Оа — проекцию отрезка данной прямой.

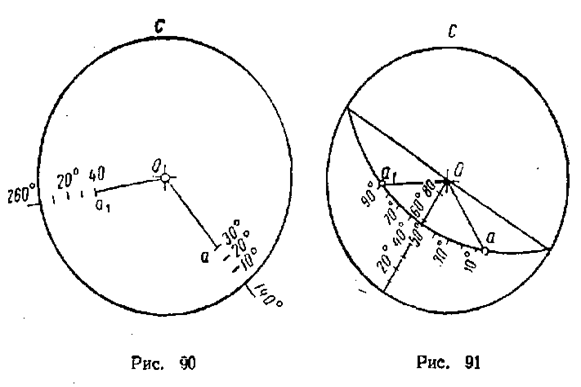
На рис. 90 отрезком Оа изображен отрезок прямой с простиранием 140° и углом наклона 30°; отрезком О а ₁ — прямая с простиранием 260° и углом наклона 40°

 

На рис. 91 приведено построение изображения плос­кости, заданной двумя прямыми с рис. 90.

Для определения угла между прямыми восковку с изображением отрезков Оа и Оа ₁ вращают так, чтобы точки а и a₁ расположились на одной дуге меридиана. Эта дуга вместе с соответствующим меридиану сетки диаметром изображает искомую плоскость. Число гра­дусов, заключенное между концами отрезков, отсчиты­вают по дуге меридиана. На рис. 91 угол между пря­мыми составляет 90⁰.

Если совместить диаметр построенной плоскости с одним из диаметров сетки, а по другому диаметру сет­ки к центру отсчитать число градусов до дуги проведенного меридиана, то получим угол падения плоскости (в примере угол равен 55°).

Для определения угла простирания устанавливают восковку в исходное положение и отсчитывают по кру­гу проекций число градусов, заключенных между север­ным полюсом сетки и направлением простирания плос­кости (в примере азимут равен 293°).

Для определения угла наклона линия пересечения.двух плоскостей Р и Q (рис. 92), азимута ее направле­ ния по восстанию и линейного угла между плоскостями строят изображение обеих плоскостей по их элементам залегания, соединяют точку пересечения соответствую­щих дуг плоскостей с центром сетки и получают проек­цию линии пересечения плоскостей; вращением восков­ки точку пересечения дуг переводят на диаметр WO сетки, по которому к центру отсчитывают число граду­сов до этой точки, что соответствует углу наклона ли­нии пересечения плоскостей. Чертеж приводят в исход­ное положение, линию пересечения продолжают до кру­га проекции, по которому от точки N, отсчитывают ази­мут ее направления.

 

 

Для определения угла между плоскостями проводят плоскость R перпендикулярно линии их пересечения. Вращением восковки точку р линии пересечения плоско­стей совмещают с диаметром сетки WO; от нее через центр сетки отсчитывают 90° и проводят дугу соответ­ствующего меридиана. Эта дуга с ее диаметром изобра­зит плоскость R. Отсчет по дуге меридиана плоскости R между точками А и В определит линейный угол между пересекающимися плоскостями Р и Q.

Сетка Каврайского позволяет удобно и просто опре­делять с достаточной точностью угловые соотношения между направлениями, плоскостями и их совокупно­стями.

Полярная стереографическая сетка. Вид полярной стереографической сетки меридианов и параллелей приведен на рис. 93, где пунктирными ли­ниями показано построение сетки.

Уравнение меридианов этой сетки — уравнение пря­мых, пересекающихся в точке полюса:

 

ходимо учитывать влияние поверхностей ослабления массива (трещины, кливаж, сланцеватость и т. д.). Прн этом элементы залегания этих поверхностей ослабле­ния замеряют во многих точках массива.

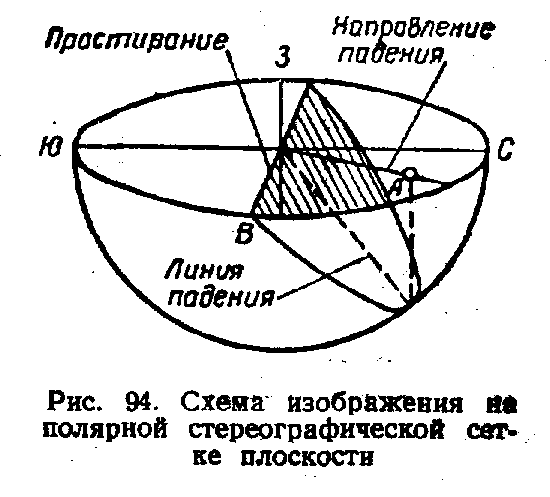
Каждую замеренную поверхность ослабления нано­сят по ее элементам залегания на полярную стереогра­фическую сетку в виде точки, для чего от северного конца вертикального диаметра сетки отсчитывают по ходу часовой стрелки азимут линии падения поверхно­сти ослабления и отмечают на внешней окружности сет­ки точку. Эту точку соединяют с центром сетки и на полученной линии, отсчитывая по параллелям от пери­ферии сетки к центру угол падения поверхности ослаб­ления, отмечают точку, определяющую данную поверх­ность ослабления.

Таким образом, каждая поверхность ослабления определится на сетке точкой А (рис. 94), представляющей

 

собой стереографическую проекцию точки пересе­чения линии падения поверхности ослабления с полу­сферой.

В результате нанесения всех поверхностей ослабле­ния на ёетку получают точечную диаграмму их распре­деления по элементам залегания.

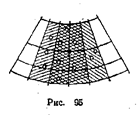
Для определения средних значений элементов зале­гания наиболее распространенных систем поверхностей ослабления данные точечной диаграммы подвергают статистической обработке. Выбирают статистическое окно, ограниченное параллелями и меридианами, отстоя­щими друг от друга на 10—30°, в зависимости от же­лательной детализации выявления концентрации поверх­ностей ослабления. После подсчета точек сетки, ока­завшихся на площадке окна, и надписи этого числа, выраженного в процентах от общего числа измерен­ных в натуре и нанесенных на диаграмму поверхно­стей ослабления, окно перемещают в соседнее положе­ние с таким расчетом, чтобы половина площади окна первого его положения была перекрыта площадью окна во втором его положении.

На рис. 95 изображена часть сетки, и на ней пока­зано штриховкой в разных направлениях два соседних положения окон подсчета. В первом положении в пре­делах окна оказалось де­вять точек, во втором — восемь. Результаты под­счета (в процентах) запи­сывают на восковке, наложенной на сетку с нанесенными на ней точками. Затем, задавшись сечением, проводят изолинии средних зна­чений концентрации поверхностей ослабления.

ВЕКТОРНЫЕ ПРОЕКЦИИ

Проекция точки. При векторном методе изображения некоторой точки А на плоскость Н точку проектируют двумя лучами: S — по перпендикуляру к плоскости Н, Т — под некоторым углом к ней (рис. 70).

 

 

Таким образом, каждой точке пространства в век­торной проекции соответст­вует направленный вектор.

Для определения поло­жения точки А в простран­стве по ее векторной проек­ции необходимо из точки а, называемой начальной про­екцией точки А, восстано­вить перпендикуляр к пло­скости Н, отложить на нем отрезок, соответствующий

расстоянию от точки а до точки А', которая называет­ся концевой проекцией точки А (рис. 71).

 

 

Проекция прямой. Проекции двух точек, произвольно взятых на прямой, дают два направленных вектора аА' и bВ' (рис. 72).

Соединив начальные проекции точек А и полу­чим а Ь — геометрическое место начальных проекций то­чек прямой — начальную проекцию прямой. Соединив концевые проекции точек А и В, получим А'В' — геометрическое место концевых проекций точек прямой —концевую проекцию прямой. Следовательно, прямая АВ в векторной проекции изобразится двумя прямыми ab и А'В' (рис. 73).

Если прямая параллельна плоскости проекции, то начальная и концевая проекции прямой параллельны (рис. 74). Прямая называется горизонталью, если основная плоскость проекции горизонтальна.

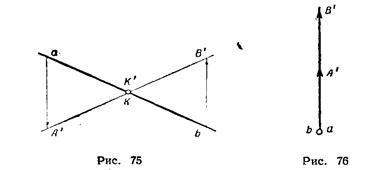
Если прямая пересекает основную плоскость проекции в пределах чертежа, то ее проекции (начальная и концевая) также пересекаются; точка пересечения по­следних определяет точку пересечения прямой с плос­костью проекции (рис. 75).

Прямая, перпендикулярная плоскости проекции, изо­бражается двумя векторами, лежащими на одной пря­мой (рис. 76).

 

 

Проекция плоскости. В векторной проекции плоскость может быть задана ее нулевой горизонталью (следом плоскости) и линией наибольшего ската.

На рис. 77 линия оо — след изображенной плоско­сти; kk' и аА' — проекция линии наибольшего ската плоскости.

Взаимоположение точек, прямых и плоскостей в век­торной проекции. 1. #очка X лежит на прямой АВ, если начало и конец вектора, изображающего данную точ­ку, лежат соответственно на начальной и концевой про­екциях прямой (рис. 78).

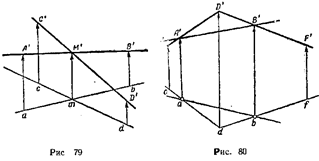
2. Две прямые А В и CD пересекаются, если вектор тМ\ изображающий точку М пересечения этих прямых, лежит соответственно своей начальной и онцевой точ­кой на пересечении начальных и концевых проекций прямых (рис. 79).

3. Прямая АВ лежит в плоскости Р, если начала (а, b) и концы (А\ В') векторов двух произвольных точек этой прямой лежат соответственно на начальных (cd, df) и концевых (C'D', D'F') проекциях прямых CD и DF, определяющих данную плоскость (рис. 80).

4.Точка А лежит в плоскости Р, если начало а и конец А ' вектора, изображающего точку А, лежат соот­ветственно на начальной аb и концевой А'В' проекциям прямой А В, лежащей в плоскости Р (рис. 80).

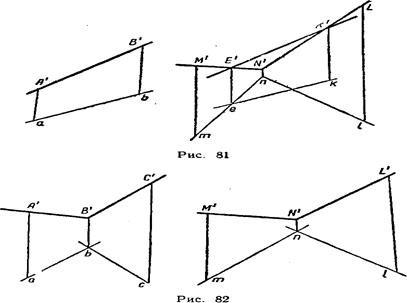
5.Прямая АВ параллельна плоскости Р, если на­чальная ab и концевая А'В' проекции этой прямой со­ответственно параллельны начальной ek и концевой Е'К’ проекциям прямой ЕК, лежащей в плоскости Р (рис. 81).

На рис. 81 плоскость Р дана векторными проекция­ми двух прямых MN и NL.

 

 

6. Две плоскости параллельны, если начальные аb и bc и концевые А'В' и В'С' проекции двух пересекаю­щихся прямых АВ и ВС одной плоскости соответственно па­раллельны началь­ным тп и пℓ и кон­цевым M'N' и N'U проекциям двух пе­ресекающихся пря­мых MN и NL другой плоскости (рис. 82).

Изображение топо­графической поверхно­сти в векторной проек­ции. На рис. 83 изобра­жен в горизонталях план участка рельефа в проекции с числовыми отметками. Для изображения его в векторной проекции на плане (рис. 83) прово­дят прямую, на которой отмечают точку со штрихом (с.-з. угол ри­сунка). На план накла­дывают восковку, копи­руют прямую и разби­вают на ней шкалу рис. 84). Деления на шкале наносят пропорционально сечению рельефа в масштабе плана и подписывают соот­ветственно отметкам горизонталей.

Совместив деление шкалы со штрихом на плане (при этом прямые на плане и на восковке должны сов­падать), копируют ту горизонталь, отметка которой одинакова с делением шкалы. Выверчивание начинают с горизонтали, у которой наибольшая отметка (65). За­тем передвигают восковку по прямой до совмещения штриха со следующим делением шкалы, перечерчивают следующую горизонталь (60) и т. д. и получают изобра­

 

жение поверхности рельефа в векторной проекции (рис. 84).

Эта проекция дает объемное изображение топогра­фической поверхности; протяженность и вид каждой горизонтали остаются теми же, что и на рис. 83.

На рис. 84 за плоскость проекции принята плоскость горизонтали 15.

Изображение горных выработок в векторной проек­ ции. Для составления векторного изображения горных выработок на исходном плане (см. рис. 64) проводят прямую, на которой сШечают стрелкой некоторую точ­ку. Затем на этот план накладывают восковку с нане­сенной на ней шкалой.

Деления шкалы пропорциональны разностям отме­ток горизонтов горных выработок. Первое деление про­порционально значению — 170—(—20) =—150 м; вто­рое деление пропорционально значению — 290 — (—170) = =—120 м.

Совместив восковку с ис­ходным планом, как указано выше, перечерчивают все гор­ные выработки верхнего гори­зонта (—20) и ствол шахты. Затем передвигают восковку по прямой так, чтобы стрелка указала на вторую точку шка­лы и перечерчивают гарные выработки следующего гори­зонта — 170 ж и т. д.

Между соответствующими точками отдельных горизонтов изображают штреки, квершла­ги и уклоны.

Эта проекция (рис. 85) дает объемное изображение горных выработок; протяженность, вид выработок и их взаимоположение на каждом отдельном горизонте остаются теми же, что и на исходном плане (см. рис. 64).

 

 

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: