Главная | Обратная связь | Поможем написать вашу работу! Архитектура Биология География Искусство История Информатика Маркетинг Математика Медицина Менеджмент Охрана труда Политика Правоотношение Разное Социология Строительство Физика Философия Финансы Химия Экология Экономика Электроника Метод среднего абсолютного прироста ⇐ ПредыдущаяСтр 11 из 16Следующая ⇒   Прогнозируемый уровень изучаемой величины изменяется в соответствии со средним абсолютным приростом этой величины в прошлом. Данный метод применяется, если общая тенденция в динамике линейна (для случая, приведенного на рисунке 32Б)     Где где 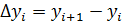y0 – базовый уровень экстраполяции выбирается как среднее значение нескольких последних значений исходного ряда - средний абсолютный прирост уровней ряда l – число интервалов прогнозирования   Пример. По данным из таблицы рассчитать прогнозное значение на t=13,14,15 В качестве базового уровня принято усредненное значение последних значений ряда, максимально трех.   t yi Δyi= yi+1-yi y0 Прогноз = y0+Δ*l                   68,2     -5 (60+75)/2=67,5 75,7       (60+75+70)/3=68,3 76,5     -3 (75+70+103)/3=82,7 90,9       (70+103+100)/3=91 99,2       (103+100+115)/3=106 114,2     -12 (100+115+125)/3=113,3 121,5       (115+125+113)/3=117,7 125,9     -2 (125+113+138)/3=125,3 133,5       (113+138+136)/3=129 137,2       (138+136+145)/3=139,7 147,9       (136+145+150)/3=143,7 143,7+8,2*1=151,9         143,7+8,2*2=160,1         143,7+8,2*3=168,3                 Метод среднего темпа роста Прогнозируемый уровень изучаемой величины изменяется в соответствии со средним темпом роста данной величины в прошлом. Данный метод применяется, если общая тенденция в динамике характеризуется показательной или экспоненциальной кривой (рисунок 32В) 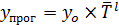  , где 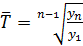– средний темп роста в прошлом l – число интервалов прогнозирования   Прогнозная оценка будет зависеть от того, в какую сторону от основной тенденции (тренда) отклоняется базовый уровень y0, поэтому рекомендуется рассчитывать y0 как усредненное значение нескольких последних значений ряда.   Пример.   t yi y0 Прогноз 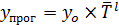,                         (60+65)/3=62,5 (65/60)1 =1,08 62,5*1,081 = 67,7     (60+65+70)/3=65 (70/60)1/2 =1,08 65*1,081 = 70,2     (65+70+68)/3=67,7 (68/60)1/3 =1,04 67,7*1,041 =70,5     (70+68+82)/3=73,3 (82/60)1/4 =1,08 73,3*1,081 =79,3     (68+82+80)/3=76,7 (80/60)1/5 =1,06 76,7*1,061 =81,2     (82+80+95)/3=85,7 (95/60)1/6 =1,08 85,7*1,081 =92,5     (80+95+113)/3=96 (113/60)1/7 =1,09 96*1,091 =105,1     (95+113+135)/3=114,3 (135/60)1/8 =1,11 114,3*1,111 =126,5     (113+135+140)/3=129,3 (140/60)1/9 =1,10 129,3*1,11 =142,1     (135+140+168)/3=147,7 (168/60)1/10 =1,11 147,7*1,111 =163,7     (140+168205)/3=171 (205/60)1/11 =1,12 171*1,121 =191,2         171*1,122 =213,8         171*1,123 =239,1

Прогнозирование на основе математических моделей

Наиболее распространенным методом прогнозирования является нахождение аналитического выражения (уравнения) тренда. Тренд экстраполируемого явления - это основная тенденцию временного ряда, в некоторой мере свободная от случайных воздействий.

Разработка прогноза заключается в определении вида экстраполирующей функции y=f(t), которая выражает зависимость изучаемой величины от времени на основе исходных наблюдаемых данных. Первым этапом является выбор оптимального вида функции, дающей наилучшее описание тренда. Наиболее часто используются следующие зависимости:

• линейная ;

• параболическая

• показательная функция

Проблемы нахождения коэффициентов линейной функции и прогноз на ее основе были рассмотрены в разделе «регрессионный анализ». Если форма кривой, описывающей тренд, имеет нелинейный характер, то задача оценки функции y=f(t) усложняется, и в этом случае необходимо привлечь к анализу специалистов по биостатистике и воспользоваться компьютерными программами по статистической обработке данных.

В большинстве реальных случаев временной ряд представляет собой сложную кривую, которую можно представить как сумму или произведение трендовой, сезонной, циклической и случайной компонент (рисунок 33).

Рисунок 33

Тренд представляет собой плавное изменение процесса во времени и обусловлен действием долговременных факторов. Сезонный эффект связан с наличием факторов, действующих с заранее известной периодичностью (например, времена года, лунные циклы). Циклическая компонента описывает длительные периоды относительного подъема и спада, состоит из циклов переменной длительности и амплитуды (например, некоторые эпидемии имеют длительный циклический характер). Случайная составляющая ряда отражает воздействие многочисленных факторов случайного характера и может иметь разнообразную структуру.

Анализ всех компонентов временного ряда и прогнозирование на их основе задача нетривиальная и требует специальной подготовки.