 |
Байесовский подход к диагностике и прогнозированию. Последовательный анализ Вальда
|
|
|
|
Когда к врачу приходит пациент, врач предварительно, основываясь на интуиции и своем опыте или знаниях о распространенности болезни в популяции, имеет некоторое предположение относительно заболевания - это априорная, или дотестовая вероятность. Далее, имея уже результаты клинического анамнеза и лабораторных тестов, он выстраивают картину болезни пациента, и увеличивает или уменьшает вероятность своего предположения – это апостериорная вероятность. В свете новых данных (например, по истечении некоторого времени лечения) апостериорная вероятность может быть пересмотрена.
Подобный алгоритм положен в основу Байесовского классификатора. Данный подход рассчитывает вероятность того, что гипотеза истинна, путем обновления предшествующих мнений о гипотезе, по мере того как новые данные становятся доступными Метод оперирует вероятностью особого типа, известной как условная вероятность. Это вероятность события при условии, что другое событие уже произошло. Например, распространенность сахарного диабета в Европе составляет 6% (вероятность 0,06), но если у конкретного пациента обнаружено повышенное содержание глюкозы в крови, то вероятность обнаружить у него сахарный диабет резко возрастает.
Апостериорная вероятность является фактически условной вероятностью гипотезы, использующей результаты исследования.
Теорема Байеса утверждает, что апостериорная вероятность пропорциональна априорной, умноженной на величину, называемую правдоподобием наблюдаемых результатов (которая описывает правдоподобие наблюдаемых результатов, если гипотеза верна).
Вероятность того, что событие А произойдет, если событие В уже произошло
|
|
|
Отношение правдоподобия положительного результата теста - это шанс положительного результата теста, если пациент имеет заболевание, деленный на шанс положительного результата теста, если он заболевания не имеет.
На формуле Байеса основана диагностическая процедура, которая использует метод последовательного статистического анализа А. Вальда. Рассмотрим суть этого метода. Пусть перед нами стоит задача выбора диагноза А или В. Известна распространенность этих заболеваний, т.е. априорные вероятности Р(А) и Р(В). После обнаружения у пациента признака х1
где 
- отношение априорных вероятностей
- отношение апостериорных вероятностей при условии обнаружения признака х1
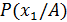- вероятность (относительная частота встречаемости) признака х1 при диагнозе А
- вероятность (относительная частота встречаемости) признака х1 при диагнозе В
-отношение правдоподобия
Тогда процесс дифференциальной диагностики выражается следующим образом
Т.е., если полученное выражение больше некоторого порогового значения А, то ставится диагноз А,если меньшенекоторого порогового значения В, то ставится диагноз В. Если ни один из порогов не достигнут, то для диагностики привлекается следующий признак х2 и проверяется неравенство
и т.д.
Если использована вся имеющаяся в распоряжении информация, и ни один из порогов так и не достигнут, то делается заключение, что информации не достаточно для постановки диагноза.
Пороговые значения устанавливаются по следующим формулам
где α – вероятность ошибки первого рода - вероятность ложно поставить диагноз В, когда на самом деле верен диагноз А
β – вероятность ошибки второго рода - вероятность ошибочно поставить диагноз А, когда на самом деле верен диагноз В
Вероятности ошибок первого и второго рода устанавливаются самим исследователем, исходя из сути решаемой проблемы.
|
|
|
Для удобства вычислений используются не сами отношения шансов, а их десятичные логарифмы, умноженные на число 10, и далее округленные до целых. Полученную величину называют диагностическим коэффициентом
Пороги также выражаются через логарифмы
Тогда алгоритм диагностики имеет следующий вид
Процесс диагностики значительно ускоряется, если использовать признаки в порядке убывания их информационной ценности. Под дифференциальной информативностью признака понимается степень различия его распределения при дифференцируемых состояниях А и В.
Удобной мерой для оценки информативности является мера Кульбаха
Если признак имеет диапазоны 
(например, возраст имеет диапазоны - дети, взрослые, пожилые), то информационная ценность всего признака
Вопрос о минимальной информативности признака еще не нашел своего решения, но некоторые авторы рекомендуют включать в процедуру прогноза признаки с 
Рассмотрим пример прогнозирования послеродовых осложнений. С этой целью были сформированы две выборки: основная (п =34) - это лица, у которых наблюдались послеродовые осложнения, и контрольная (без осложнений), в которую вошли 32 роженицы. Всего исследовано 20 признаков, которые имели от 2 до 3 диапазонов. Результаты всех расчетов приведены в таблице.
| № | Факторы риска
| 
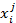
| Число случаев | 
| 
| Р/Р | ДК | 
| 
| |
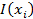
| Осн.гр.(A) п =34 | Контр. гр.(B) п =32 | |||||||||
| Мед аборты до настоящих родов 1-2 | есть | 0,206 | 0,094 | 2,196 | 0,19 | 0,22 | ||||
| нет | 0,794 | 0,906 | 0,876 | -1 | 0,03 | |||||
| Самопроизвольные выкидыш до настоящих родов | есть | 0,265 | 0,125 | 2,118 | 0,23 | 0,28 | ||||
| нет | 0,735 | 0,875 | 0,840 | -1 | 0,05 | |||||
| Патология шейки матки | есть | 0,147 | 0,125 | 1,176 | 0,01 | 0,01 | ||||
| нет | 0,853 | 0,875 | 0,975 | 0,00 | ||||||
| Бесплодие в анамнезе | есть | 0,176 | 0,031 | 5,647 | 0,55 | 0,59 | ||||
| нет | 0,824 | 0,969 | 0,850 | -1 | 0,05 | |||||
| Многоплодная беременность | есть | 0,176 | 0,094 | 1,882 | 0,11 | 0,13 | ||||
| нет | 0,824 | 0,906 | 0,909 | 0,02 | ||||||
| Токсикозы | в первой половине | 0,618 | 0,500 | 1,235 | 0,05 | 0,35 | ||||
| во второй половине | 0,235 | 0,188 | 1,255 | 0,02 | ||||||
| нет | 0,147 | 0,313 | 0,471 | -3 | 0,27 | |||||
| ОРВИ | 1 триместре | 0,500 | 0,156 | 3,200 | 0,87 | 2,84 | ||||
| 2 триместре | 0,059 | 0,063 | 0,941 | 0,00 | ||||||
| 3 триместре | 0,294 | 0,125 | 2,353 | 0,31 | ||||||
| нет | 0,147 | 0,656 | 0,224 | -7 | 1,65 | |||||
| Резус конфликт | есть | 0,088 | 0,031 | 2,824 | 0,13 | 0,14 | ||||
| нет | 0,912 | 0,969 | 0,941 | 0,01 | ||||||
| Хронические генитальные инфекции | есть | 0,706 | 0,469 | 1,506 | 0,21 | 0,51 | ||||
| нет | 0,294 | 0,531 | 0,554 | -3 | 0,30 | |||||
| Маловодие | есть | 0,382 | 0,281 | 1,359 | 0,07 | 0,10 | ||||
| нет | 0,618 | 0,719 | 0,859 | -1 | 0,03 | |||||
| Многоводие | есть | 0,500 | 0,344 | 1,455 | 0,13 | 0,22 | ||||
| нет | 0,500 | 0,656 | 0,762 | -1 | 0,09 | |||||
| Преждевременные роды | есть | 0,147 | 0,031 | 4,706 | 0,39 | 0,42 | ||||
| нет | 0,853 | 0,969 | 0,880 | -1 | 0,03 | |||||
| Кесарева сечение | есть | 0,206 | 0,063 | 3,294 | 0,37 | 0,42 | ||||
| нет | 0,794 | 0,938 | 0,847 | -1 | 0,05 | |||||
| Родостимуляция | есть | 0,147 | 0,063 | 2,353 | 0,16 | 0,17 | ||||
| нет | 0,853 | 0,938 | 0,910 | 0,02 | ||||||
| Аномальное предлежание | есть | 0,118 | 0,031 | 3,765 | 0,25 | 0,27 | ||||
| нет | 0,882 | 0,969 | 0,911 | 0,02 | ||||||
| Воды грязные | есть | 0,471 | 0,125 | 3,765 | 1,00 | 1,37 | ||||
| нет | 0,529 | 0,875 | 0,605 | -2 | 0,38 | |||||
| Отслойка плаценты | есть | 0,176 | 0,063 | 2,824 | 0,26 | 0,29 | ||||
| нет | 0,824 | 0,938 | 0,878 | -1 | 0,03 | |||||
| Преждевременные излитие околоплодных вод | есть | 0,294 | 0,031 | 9,412 | 1,28 | 1,46 | ||||
| нет | 0,706 | 0,969 | 0,729 | -1 | 0,18 | |||||
| Низкая плацентация | есть | 0,235 | 0,063 | 3,765 | 0,50 | 0,57 | ||||
| нет | 0,765 | 0,938 | 0,816 | -1 | 0,08 | |||||
| Сильное шевеление | есть | 0,529 | 0,188 | 2,824 | 0,77 | 1,18 | ||||
| нет | 0,471 | 0,813 | 0,579 | -2 | 0,41 |
|
|
|
В таблице ниже приведены первые 7 признаков, расположенные по мере убывания их и информационной ценности
| № | |||||||
| xi | ОРВИ | Преждевр. излитие околоплодных вод | Воды грязные | Сильное шевеление | Бесплодие в анамнезе | Низкая плацентация | Хрон. генитальные инфекции |
|
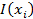
| 2,84 | 1,46 | 1,37 | 1,18 | 0,59 | 0,57 | 0,52 |
Из этой таблицы видно, что наиболее значимыми признаками послеродовых осложнений являются перенесенные ОРВИ, преждевременное излитие околоплодных вод, сильное шевеление плода и т.д.
|
|
|
Для реализации алгоритма прогноза в данном исследовании были заданы:
α – вероятность ошибки первого рода = 0,05
β – вероятность ошибки второго рода = 0,1
К вероятности α более жесткие требования, поскольку речь идет о том, что ошибочно не будут спрогнозированы послеродовые осложнения.
Тогда
Т.к. по литературным данным послеродовые осложнения достигают до 26% (априорная вероятность), то
Осуществим прогноз для пациентки со следующими признаками:
|
|
|
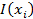
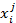
| ДК | 
|
| ОРВИ | 2,84 | 1 триместр | -5+5=0 | |
| Преждевременные излитие околоплодных вод | 1,40 | нет | -1 | -5+5-1=-1 |
| Воды грязные | 1,32 | есть | -5+5-1+6=5 | |
| Сильное шевеление | 1,18 | есть | -5+5-1+6+5=10 | |
| Бесплодие в анамнезе | 0,59 | нет | -1 | |
| … | … | … | … | … |
Уже на четвертом шаге превышается верхний порог и прогнозируются послеродовые осложнения.
|
|
|
