Лекция 3. Математические методы теории очередей.

Важным этапом в применении теории массового обслуживания является формальное описание функционирования этого объекта в терминах системы массового обслуживания (СМО). СМО считается заданной, если полностью описаны следующие ее компоненты:

- входящий поток запросов (заявок, требований, сообщений, вызовов);

- количество и типы обслуживающих устройств (приборов);

- емкости накопителей (буферов), где запросы, заставшие все приборы занятыми, ожидают начало обслуживания;

- времена обслуживания запросов на приборах;

- дисциплина обслуживания (она определяет порядок обработки запроса в системе, начиная с момента его поступления в систему и до момента, когда он покидает СМО).

Согласно символике Дж. Кендалла, введенной в 1953 году, в теории массового обслуживания принято кодирование основных СМО в виде совокупности четырех символов, разделенных вертикальными чертами: А|B|n|m. Символ n, n³ 1 задает число идентичных параллельных обслуживающих устройств. Символ m, m³0 задает число мест для ожидания в буфере. Если m=¥, то четвертый символ в описании СМО может отсутствовать. Символ А описывает входящий поток запросов, а символ В – распределение времен обслуживания запросов.

Входящий поток во многом определяет характеристики производительности функционирования СМО. Поэтому правильное описание потока запросов, поступающих в случайные моменты времени в реальную систему, и идентификация его параметров являются весьма важной задачей. Во входящем (случайном) потоке, запросы поступают в систему в некоторые случайные моменты времени t₁, t₂, …,t_n,…. Будем обозначать t_k = t_k-1 длину интервала между моментами поступления (k-1) -го и k –го запросов, k ³ 1 (t₀ полагается равным 0) и х_t – число моментов t_k.

Случайный поток считается заданным, если задано совместное распределение величин t_k, k=1,…,n для любого n, n³1 или задано совместное распределение величин x_t для всех значений t, t³0.

Определение 1. Случайный поток называется стационарным, если для любого числа m и любых неотрицательных чисел u₁,…,u_m совместное распределение величины (x_t+uk – x_t),k=1,…,m не зависит от величины t.

Определение 2. Случайный поток называется ординарным, если для любого t имеет место соотношение

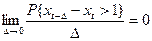
Определение 3. Говорят, что случайный поток является потоком без последствия, если числа заявок, поступивших на непересекающихся интервалах времени, являются независимыми в совокупности случайными величинами.

Определение 4. Случайный поток называется потоком с ограниченным последействием, если величины t_k, k³1 независимы в совокупности.

Определение 5. Случайный поток называется рекуррентным потоком, если поток является потоком с ограниченным последействием и величины t_k, k³1 одинаково распределены.

Их функцию распределения будем обозначать А(t) = P {t_k <t}. Функция А(t) полностью характеризует рекуррентный поток.

Если распределение А(t) – показательное: А(t) = 1- е^-lt, то первый символ принимает значение М.

Если распределение А(t) вырожденное, то есть запросы поступают через равные промежутки времени, то первый символ принимает значение D.

Если распределение А(t) – гиперэкспоненциальное, то первый символ принимает значение HMn.

Если распределение А(t) – эрланговское с параметрами (l, k), то первый символ принимает значение Ek.

Если о виде функции распределение А(t) не делается никаких предположений, то первый символ принимает значение G или GI.

Определение 6. Интенсивностью l стационарного случайного потока называется математическое ожидание (среднее значение) числа запросов, поступающих в единицу времени:

.

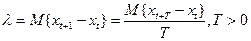Определение 7. Параметром a стационарного случайного потока называется положительная величина, определяемая соотношением:

.

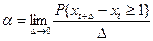Определение 8. Стационарный ординарный поток без последствий называется простейшим.