 |
Лекция 4. Модели анализа ВС. Однофазная модель ВС
|
|
|
|
Наиболее хорошо исследованными являются однолинейные однофазные системы массового обслуживания с простейшим входящим потоком и показательным распределением времени обслуживания. Это объясняется тем, что процессы, которые в первую очередь интересуют исследователей, а именно: Число запросов в системе в момент времени t, время ожидания запроса wt, который поступит (или может поступить) в момент времени t и др., являются одномерными и являются Марковскими.
Рассмотрим систему типа М/М/1 – это однолинейная СМО с ожиданием (буфером неограниченной емкости), в которую поступает простейший поток запросов интенсивности λ, а время обслуживания запросов имеет показательной распределение с параметром μ.
Анализируя поведение этой системы легко установить, что процесс it –число запросов в системе в момент t – является процессом гибели и размножения с параметрами:


Определение. Заявка ВС - запрос на выполнение всех видов работ по обслуживанию запроса.
В результате обслуживания запроса в системе выполняется комплекс программ реализующих весь набор обращений к ресурсам системы.
Для модели массового обслуживания (ММО) важно время обслуживания. Данная переменная в моделях ММО, может быть величиной детерминированной или случайной (заданной наперед).
В ММО используют гипотезу, что все времена обслуживания как правило подчиняются экспоненциальному закону распределения, который предполагает следующее:
1. Стационарность-неизменность средних величин;
2. Вероятность появления на интервале времени не более одного события;
3. Отсутствия последствия, т.е. нет влияния текущего события на последующие.
Пуассоновский закон распределения заявок описывает количество событий на интервале времени и описывает интенсивности этих событий. В ММО речь может вестись о стационарных и нестационарных режимах.
|
|
|
Стационарные режимы - это режимы обслуживания, в которых среднее число заявок не меняется. В противном случае речь идет о нестационарной системе. В целом ММО могут быть представлены в виде замкнутой и разомкнутой стохастических систем. Принципы построения таких моделей обусловлены спецификой моделирования тех или иных процессов.
Параметры однофазной модели (состав модели):
 - интенсивность поступления заявок
- интенсивность поступления заявок
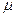 - интенсивность обслуживания
- интенсивность обслуживания
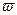 - производительность системы
- производительность системы
 - среднее время выполнения программы обработки
- среднее время выполнения программы обработки
 - коэффициент загрузки
- коэффициент загрузки
К - емкость буфера в количестве заявок

Если  , то система стационарна и
, то система стационарна и 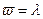 , если
, если  , то система не стационарна, а w=m.
, то система не стационарна, а w=m.
Стационарная система характеризуется постоянным средним количеством заявок в системе. Среднее число заявок в системе равно среднему числу заявок на обслуживании плюс среднее число заявок в очереди.
При ρ<1, среднее число ожидающих заявок является величиной стационарной.
При ρ>1, средняя очередь является бесконечно возрастающей. При конечном значении К возможна ситуации переполнения буфера памяти. Эти ситуации вызывают потерю входных заявок.
Кроме числа фаз модели массового обслуживания и параметров интенсивности обслуживания в качестве параметра определяется число линий по каждой фазе. Они определяются числом обслуживающих приборов в данной фазе.
Осн. лит. 1[34-38],
Доп. лит.5[16-28].
Контрольные вопросы:
1. Условие стационарности однофазной СМО.
2. Пуассоновский закон распределения.
3. Параметры однофазной модели.
4. Чем определяется число линий по каждой фазе?
Лекция 5. Анализ модели однолинейной однофазной системы массового обслуживания
 Б
Б
К 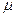
|
|
|
Рисунок 5.1- Схема однолинейной однофазной СМО
Предполагается, что времена обслуживания в фазе и интервалы поступления заявок являются случайными величинами (с экспоненциальным законом распределения).
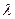 - интенсивность поступления входных запросов. Порядок последовательный. Закон поступления описывается Пуассоновским распределением. Поступающие запросы поступают в буфер Б – бесконечной емкости. Порядок обслуживания в очереди естественный (FIFO). Рассмотренная модель предполагает размер очереди К=
- интенсивность поступления входных запросов. Порядок последовательный. Закон поступления описывается Пуассоновским распределением. Поступающие запросы поступают в буфер Б – бесконечной емкости. Порядок обслуживания в очереди естественный (FIFO). Рассмотренная модель предполагает размер очереди К=  . Запросы на обслуживание берутся из очереди, при чем обслужится может только одна заявка. Вероятность состояния Pn систем показывает вероятность, когда в системе находится ровно n-заявок.
. Запросы на обслуживание берутся из очереди, при чем обслужится может только одна заявка. Вероятность состояния Pn систем показывает вероятность, когда в системе находится ровно n-заявок.
Для каждого состояния, согласно материалу из лекции 3, можно составить систему уравнений баланса:
 , для n=1,¥ (5.1)
, для n=1,¥ (5.1)
Решив системы уравнений с применением условие нормировки:
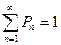 (5.2)
(5.2)
получаем:

для r=1,¥
По найденным вероятностям находятся характеристики однофазной СМО с бесконечным буфером.
Среднее число запросов в системе:

Отсюда следует, что в произвольный момент времени система простаивает с вероятностью 1-ρ.
Средняя длина очереди:

Среднее время ожидания запроса в очереди:
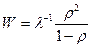
Среднее время пребывания запроса в системе(то есть, времени с момента поступления в систему до момента окончания обслуживания на приборе):

На основании данных расчетов можно решить среднее число запросов в системе и среднюю длину очереди по другому:

Данный показатель характеризует время с момента поступления в систему до момента окончания обслуживания на приборе и складывается из времени ожидания в очереди и времени обслуживания.
Все эти характеристики справедливы и для многих, более общих систем. Вышеперечисленные характеристики являются формулами Литтла.
Осн. лит. 1[34-38],
Доп. лит.5[16-28].
Контрольные вопросы:
1. Как влияет емкость буфера на характер приема поступающих заявок.
2. Что такое однофазная многоканальная СМО?
3. Из чего складывается время ожидания в очереди?
4. Что описывает формулы Литтла?
|
|
|


