Маршрутная матрица и потоки в сетях

Переход сообщения из одного центра после окончания обслужи­вания в нем в другой осуществляется в соответствии с заданным маршрутом, под которым понимается последовательность посеща­емых сообщением центров сети. Маршрут сообщения по сети МО задается матрицей маршрутов Р, вид которой зависит от того, яв­ляется ли сеть МО открытой или замкнутой. В открытую сеть МО сообщения поступают из внешнего источника и могут покидать сеть после завершения обслуживания. Если принять внешний источник за новый центр сети и обозначить индексом 0, то маршрут в откры­той сети задается стохастической неразложимой матрицей P=|| P_ij ||, где P_J0и P_0j - соответственно вероятность поступления в j-ыйцентр сообщения из источника и вероятность покидания сообщением се­ти после окончания обслуживания в j-томцентре (j = 1,М); P_ij - вероятность того, что сообщение, уходящее из i-го центра, перейдет в ji-й центр (i,j = 1,М). Очевидно, что выполняется равенство S_j=0^M P_ij=1 (i = 0,1,...,М), где P₀₀₌₀ (предположение P₀₀¹0 не представляет практического интереса).

Входящий из источника в сеть поток сообщений определяется сов­местным распределением случайных величин Z_R=t_R-t_R-1, где t_R - моменты поступления сообщений (R ³ 1, t₀ =0, 0 £ t₁ £ t₂ £…). Если случайные величины Z_Rнезависимы в совокупности, то та­кой поток называют потоком с ограниченным последействием и для его определения достаточно задать набор функций распределения H_R(t)=P{Z_R £ t}, R³ 1. Важную роль в теории систем и сетей МО играет рекуррентный поток, для которого H₁ (t) = H₂ (t) = …= H (t). Очевидно, что частным случаем рекуррентного потока является пуассоновский поток, для которого H (t) = 1-e^-lt, где интенсивность потока l может зависеть от общего числа сообщений N, находящихся в сети.

Для определения потоков, циркулирующих в стационарном ре­жиме в открытой сети МО, введем коэффициенты передачи e_iтакие, что e_il(N)представляет собой общую интенсивность потока сообще­ний в i-й центр сети (i = 1,М). Легко видеть, что интенсивность e_il(N)складывается из интенсивности поступления сообщений в i-й центр из источника P_0il (N) и интенсивностей поступления из других центров e_jP_ijl(N) (j = 1,М). Таким образом, величины e_iудовле­творяют следующей системе линейных уравнений:

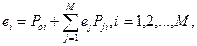(9.1)

В замкнутой сети МО сообщения извне не поступают и не по­кидают сеть; количество сообщений, циркулирующих в ней, посто­янно и равно N. Матрица Р, определяющая случайные маршруты движения сообщений, так же как и для открытой сети, предпола­гается стохастической и неразложимой, но не содержит в этом слу­чае нулевых столбца и строки (источник сообщений отсутствует) и (i=1,M) Система линейных уравнений (9.1) преоб­разуется к виду

(9.2)

Число независимых уравнений в системе (9.2) на единицу мень­ше количества переменных, так что ее решение единственно с точ­ностью до мультипликативной константы. Другими словами, если - решение системы уравнений (9.2), то при решением является и . Для отыскания однозадачного решения системы уравнений (9.2) достаточно произвольно задать значение е_i, например, положить . В этом случае величину можно интерпретировать как среднее число посещений со­общением центра j (j = ) между двумя последовательными посещениями им первого центра.

Пусть - поток, проходящий через i -й центр (i = ) в стаци­онарном режиме. Тогда очевидное выражение связывает потоки, проходящие через i -й и первый центры сети.

В силу статической однородности сообщений, циркулирующих в замкнутых стохастических сетях, такие сети называют однородными. При этом однородную сеть МО будем называть экспоненциальной, если функция распределения является экспоненциальной и немарковской, и если хотя бы одна из этих функций является произвольной.

Естественным обобщением однородных сетей МО являются сети с несколькими классами сообщений, отличающимися как маршрутами, так и длительностями обслуживания в центрах. Такая сеть может быть открытой, замкнутой или смешанной. Смешанная сеть МО открыта для одних классов сообщений, которые поступают в нее из вне и после окончания обслуживания покидают ее, и замкнута для других классов (количество сообщений каждого из таких классов внутри сети постоянно).

Основные подходы к исследованию сетей МО с несколькими классами базируется либо на прямом методе отыскания выражений для вероятностей состояний сети с использованием техники составлений уравнений баланса, либо на методике составления рекуррентных уравнений для средних значений.

Перечисленные методы позволяют находить точное решение для мультипликативных или локально-сбаллансированных сетей, вероятности состояний которых имеют мультипликативный вид.

Осн. лит. 1[90-104],

Доп. лит.5[33-47].

Контрольные вопросы:

1. Компоненты замкнутой стохастической сети.

2. Как задается маршрут прохождения заявки по сети?

3. Что такое число посещений сообщением центра обслуживания?

4. Чем определяются интенсивности потоков в замкнутой сети?

5. Как определяются потоки, циркулирующие в замкнутой сети?