 |
Глава 4. Этапы автоматизированного расчета конструкций на сейсмические воздействия
|
|
|
|
Глава 4. Этапы автоматизированного расчета конструкций на сейсмические воздействия
4. 1. Определение эквивалентной жесткости здания
Важной задачей является определение эквивалентной жесткости стержня. Для этого предлагается использовать условие равенства удельного перемещений точек A1 и A2 (рис. П1, а, б) при действии эквивалентных нагрузок. При этом, в случае перемены сечений колонн по высоте здания, необходимо учитывать это при определении значения эквивалентной жесткости.
(а) (б) (в)
Рис. 4. 1
К определению эквивалентной жесткости стержня
Величину перемещения 
следует определять из статического расчета конечно-элементной модели здания. Перемещение 
определяется по формуле Мора-Максвелла (рис. П2, в):
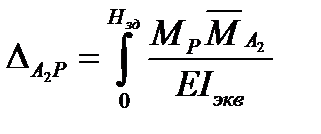. (4. 1)
Раскроем интеграл (П1) с помощью правила Верещагина:
. (4. 2)
Условие эквивалентности жесткостей примет вид:
, (4. 3)
или, с учетом (П2):
, (4. 4)
откуда
. (4. 5)
При этом можно задаваться любой величиной силы P, учитывая, что величина перемещения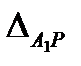 
всегда пропорциональна ей. Для повышения точности расчета рекомендуется выбирать силу P таким образом, чтобы перемещение 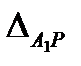не было исчезающее мало.
Рассмотрим решение задачи по определению эквивалентной жесткости на примере шестнадцатиэтажного каркасного здания. Для определения эквивалентной жесткости стержня был построена конечно-элементная модель в ПВК SCAD. Результаты статического расчета от воздействия единичной горизонтальной силы приведены на рис. П2.
|
|
|
Рис. 4. 2
Горизонтальные перемещения точек здания (мм)
С учетом полученного перемещения верхней точки здания, используя формулу (4. 5), получаем: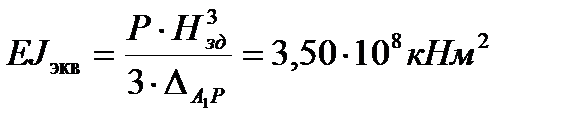 
.
4. 2. Определение форм собственных колебаний
Рассмотрим процесс определения форм собственных колебаний на примере системы с двумя степенями свободы (рис. 4. 3). Жесткости всех стержней EJ=104 кНм2, масса М=2т. Для определения удельных перемещений строим эпюры моментов от единичных сил, определяющих степени свободы системы (рис. 4. 3).
Рис. 4. 3
Эпюры моментов от единичных сил
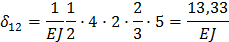
Уравнение частот принимает вид:
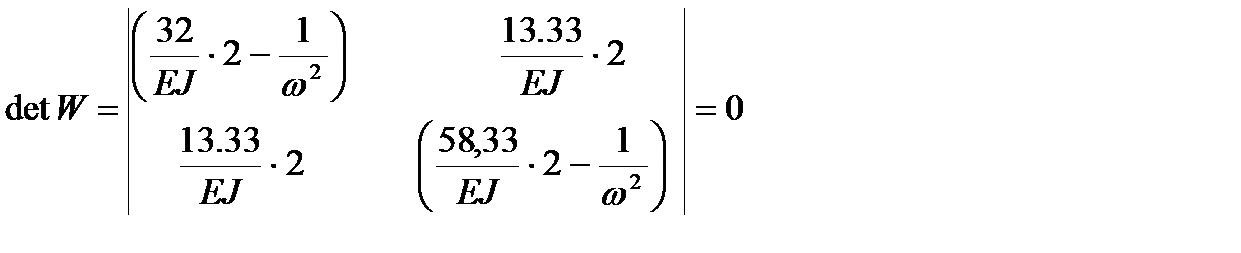
В результате раскрытия определителя получаем 
=8, 85 сек-1, 
= 13, 75 сек-1.
Принимая коэффициент формы в направлении первой степени свободы при первой частоте 
, определяем коэффициент формы в направлении второй степени свободы: 
.
Проверка значения – по формуле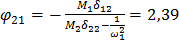 
.
Строим первую форму собственных колебаний (рис. 4. 4), откладывая в масштабе амплитудные значения колебаний – для направления первой степени свободы - , для направления второй степени свободы - 
. Представляем отклоненные положения рамы.
Рис. 4. 4
Первая форма собственных колебаний
Аналогично для частоты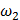 
находим 
. Строим вторую форму собственных колебаний (рис. 4. 5).
Рис. 4. 5.
Вторая форма собственных колебаний
4. 3. Определение сейсмических нагрузок на каркасное здание
4. 3. 1. Исходные данные
Рис. 4. 6 – План несущих конструкций на отм. 0, 000
Рис. 4. 7 – Разрез
4. 4. Определение динамических характеристик здания
4. 4. 1. Определение масс в уровнях перекрытий при двух загружениях
| (1) |
где: 
- нагрузка на i-перекрытие;
|
|
|
– площадь i-го перекрытия;
– ускорение свободного падения.
1-ое сочетание нагрузок:
Постоянная нагрузка = 1, 9 кПа;
Длительная нагрузка = 2, 9 кПа.
2-ое сочетание нагрузок:
Постоянная нагрузка = 1, 9 кПа;
Длительная нагрузка = 2, 9 кПа;
Полезная нагрузка = 3, 8 кПа;
Снеговая нагрузка = 0, 5 кПа.
I загружение:
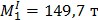
| II загружение:
|
|
|
|
