 |
Глава 5. Расчет трехэтажного железобетонного здания на сейсмические
|
|
|
|
Глава 5. Расчет трехэтажного железобетонного здания на сейсмические
воздействия. Неавтоматизированное проектирование
По спектральному методу определим величину сейсмических сил и построим эпюры изгибающих моментов и поперечных сил по высоте трехэтажного дома, предполагая, что интенсивность сейсмического воздействия равна 9 баллам по шкале MSK-64. т. е. 
=0, 4g. Грунты основания являются суглинками с характеристиками: 
, 
, 
.
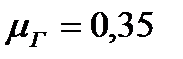Трехэтажный железобетонный дом, расчетная схема которого представлена на рис1., характеризуется следующими параметрами: 
, 
, 
. Размеры сооружения в плане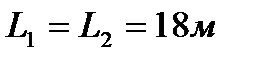 
. Логарифмический декремент затухания колебания принимается равным 
.
Рис. 5.
5. 1. Определение частоты собственных колебаний при горизонтально-вращательном движении здания, предполагая его абсолютно жестким телом
Скорости распространения продольных и поперечных сил грунтов принимают значения:
;
Далее определим квазистатические жесткости основания при сдвиговом и вращательном движении здания:
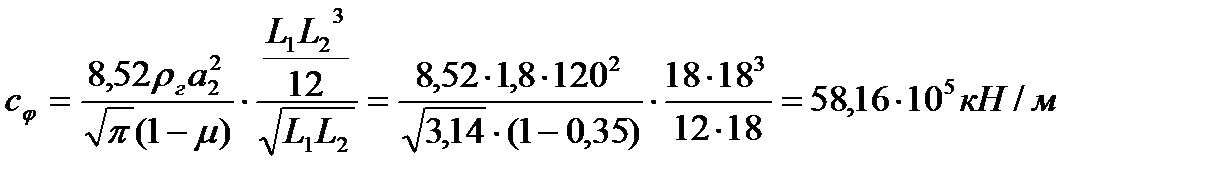
Определим общую массу здания и момент инерции сосредоточенных масс относительно центра вращения, т. е. относительно центра подошвы фундамента сооружения:
;
Частоты собственных колебаний здания в виде жесткого тела при горизонтальном и вращательном движениях принимают значения:
;
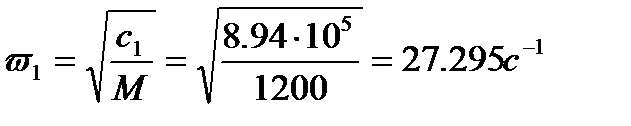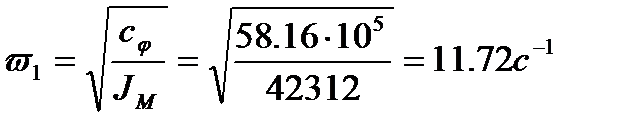
5. 2. Определение собственных частот колебания здания при одновременном учете изгибных и сдвиговых деформаций конструкции, без учета
податливости основания
Единичные эпюры моментов и поперечных сил изображены на Рис1.
Применяя формулу Мора с учетом эпюры моментов и поперечных сил, изображенных на Рис1, последовательно вычисляются:
|
|
|
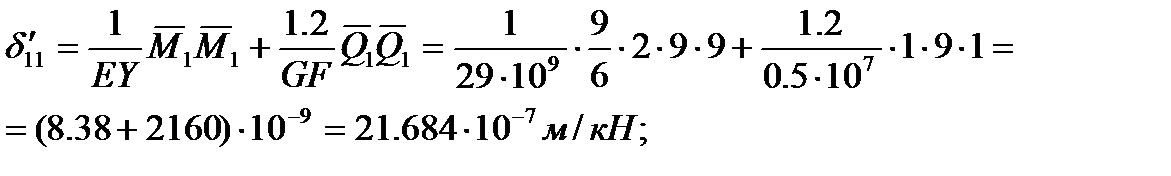
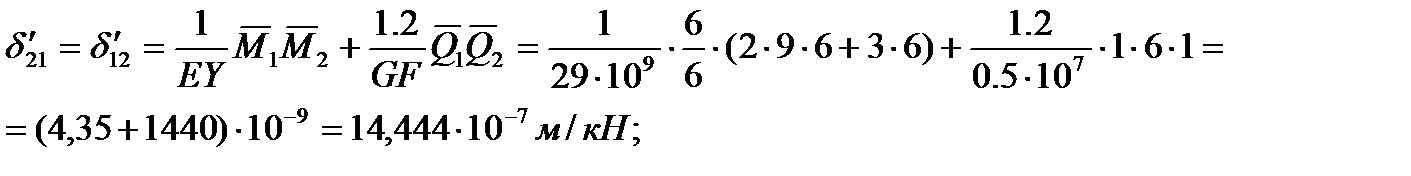
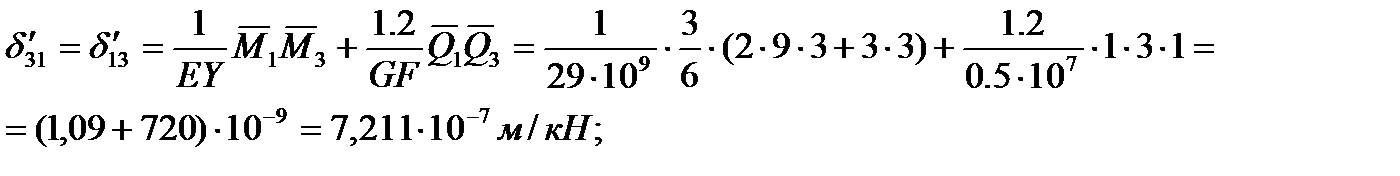
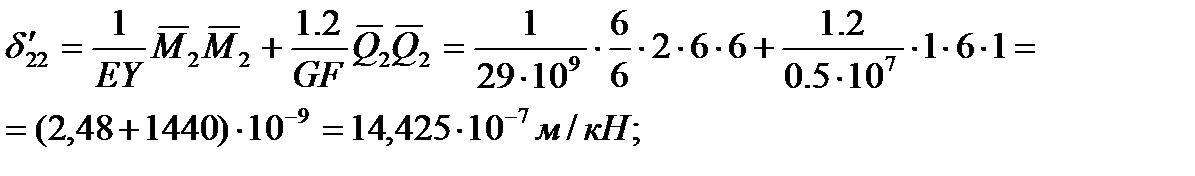
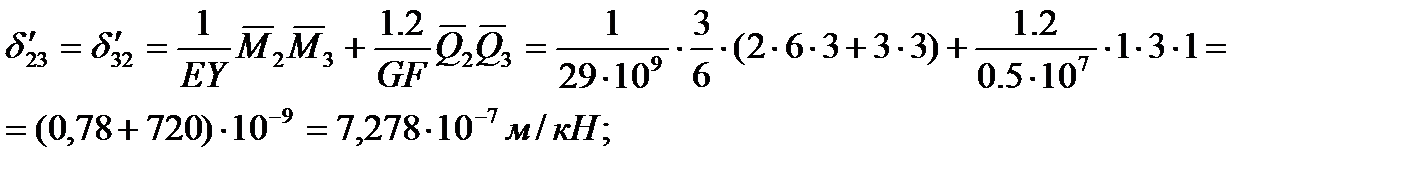
Для определения собственных частот воспользуемся частотным уравнением:
Делим каждый член последнего уравнения на 
и принимаем обозначение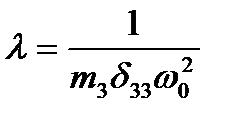 
, получим:
Коэффициенты кубического уравнения имеют следующие значения: a=1; b=-6; c=5; d=-1.
Для определения корней кубического уравнения по методу Кардано вводим следующие обозначения:
т. к. 
то 
Учитывая, что 
, имеем: 
Далее:
В возрастающем порядке 
определим частоты собственных колебаний здания без учета диссипативных свойств здания:
Собственная частота колебания здания с учетом диссипативных свойств здания принимает значение:
5. 3. Определение собственных значений, проверка ортогональности между различными формами колебания и построение формы колебания
Для первой формы колебаний имеем:
Последовательно вычисляем коэффициенты при неизвестных:
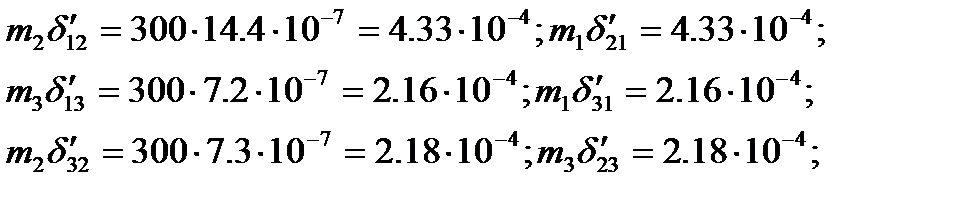
Подставляя коэффициенты и умножая каждый член уравнения на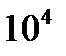 
, получим:
Так как данная система представляет собой систему однородных алгебраических уравнений, поэтому определяются относительные величины неизвестных. Полагая, что 
=1 из первых двух уравнений получим:
Решая данную систему уравнений, получим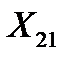 
=0, 8; 
=0, 44.
Для определения собственных значений, по второй форме колебаний здания, предварительно определим коэффициенты при неизвестных, содержащих собственные частоты:
Уравнение относительно собственных векторов по второй форме колебания принимают вид:
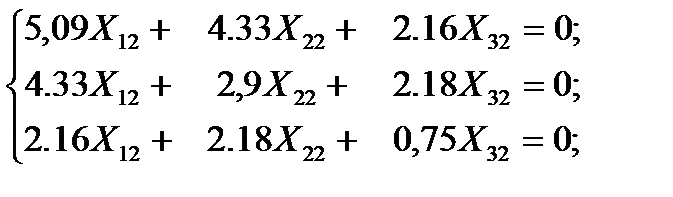
Принимая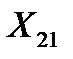 
=1, первые два уравнения последней системы преобразуются в виде:
Из решения последней системы определяются: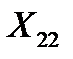 
=-0, 53; 
=-1, 25.
Для определения собственных значений, третьей форме колебаний здания, предварительно определим:
Система уравнений относительно собственных значений принимает вид:
Полагая 
=1, из двух первых уравнений, получим:
|
|
|
Отсюда: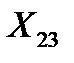 
=-2, 26; 
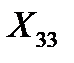=1, 82.
Учитывая что 
, условие ортогональности между первой и второй формой записывается в следующем виде:
Условие ортогональности между первой и третьей формой:
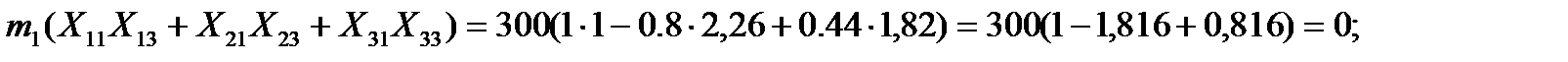Условие ортогональности между второй и третьей формой:
Рис. 5. 3. 1 Формы колебания системы.
|
|
|
