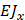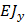 |
4.4.2.Определение эквивалентной жесткости здания
|
|
|
|
4. 4. 2. Определение эквивалентной жесткости здания
| (2) |
где: 
- вспомогательная единичная нагрузка, прикладываемая в уровне покрытия.
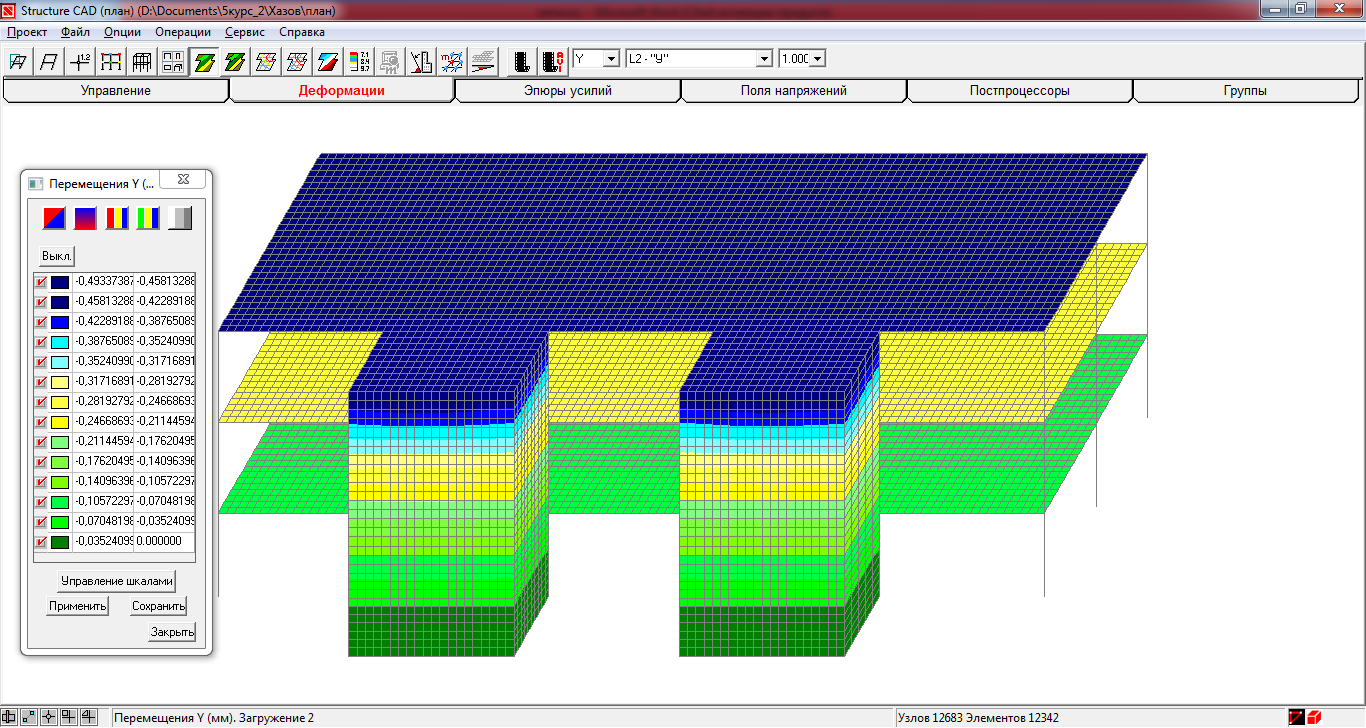
Рис. 4. 8
Горизонтальное перемещение вдоль оси у (мм)
Рис. 4. 9
Горизонтальное перемещение вдоль оси х (мм)
4. 4. 3. Составляем матрицу податливости
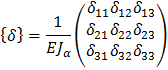
| (3) |
где δ ij – удельное перемещение точки сосредоточения i-ой массы от единичной силы, приложенной в точке сосредоточения j-ой массы. Для определения элементов матрицы податливости воспользуемся программно-вычислительным комплексом Полюс (рис. П10).
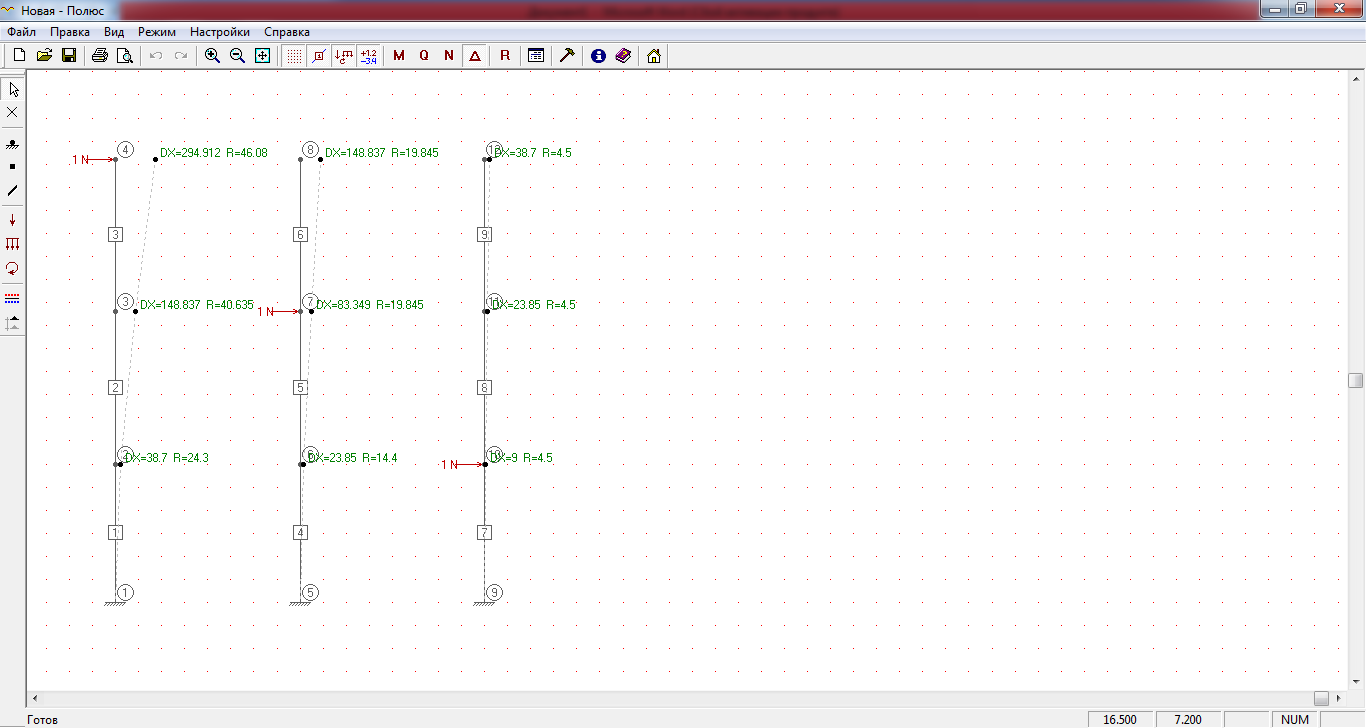
Рис. П10
К определению матрицы податливости
4. 4. 4. Определяем круговую частоту собственных колебаний
Составляем матрицу масс:
| (4) |
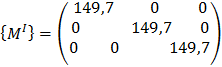
Уравнение колебаний имеет вид:
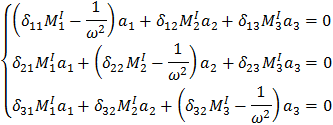
| (5) |
Составляем матрицу частот:
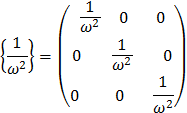
| (6) |
Система уравнений (5) имеет нулевое решение (ai=0), которое соответствует отсутствию колебаний и не имеет смысла в поставленной задаче, а так же ненулевое решение, которое существует только при выполнении условия:
detA 
| (7) |
Решение условия (7) находим с помощью комплекса электронных таблиц Microsoft Excelм путем перебора различных значений ω . Повторяем данную операцию для всех загружений при двух направлениях колебаний (для жесткостей 
и 
).
Результаты вычислений динамических характеристик здания сводим в таблицу 1.
Табл. 1 – Результаты вычислений динамических характеристик здания
| загруж. | относит. | относит. | ||||||
| 
| 
| 
| 
| 
| |||
|
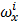
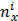
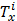
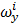
I | 5, 692 | 0, 9059 | 1, 1038 | 38, 218 | 6, 0825 | 0, 1644 | ||
| 37, 418 | 5, 9552 | 0, 1679 | 251, 242 | 39, 9864 | 0, 0250 | |||
| 100, 087 | 15, 9294 | 0, 0627 | 672, 018 | 106, 9549 | 0, 0093 | |||
|
II | 4, 1595 | 0, 6620 | 1, 5105 | 27, 928 | 4, 4448 | 0, 2249 | ||
| 27, 803 | 4, 4249 | 0, 2259 | 186, 678 | 29, 7107 | 0, 0336 | |||
| 74, 724 | 11, 8926 | 0, 0840 | 501, 726 | 79, 8521 | 0, 0125 | |||
4. 4. 5. Определение коэффициентов форм собственных колебаний
Учитывая уравнение (7) и систему уравнений (5), имеем бесконечное множество решений.
Выразим все амплитуды через амплитуды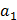 
, тогда неизвестными будут являться отношения:
| (8) |
где: i – номер массы(этажа);
k – номер формы собственных колебаний.
Система уравнений примет вид:
Получаем 3 системы из 2-х уравнений с двумя неизвестными:
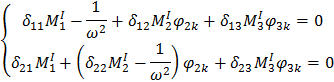
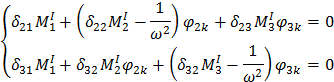
4. 4. 6. Определение форм для I загружения
Относительно ОХ и ОУ:
1 форма собственных колебаний
2 форма собственных колебаний
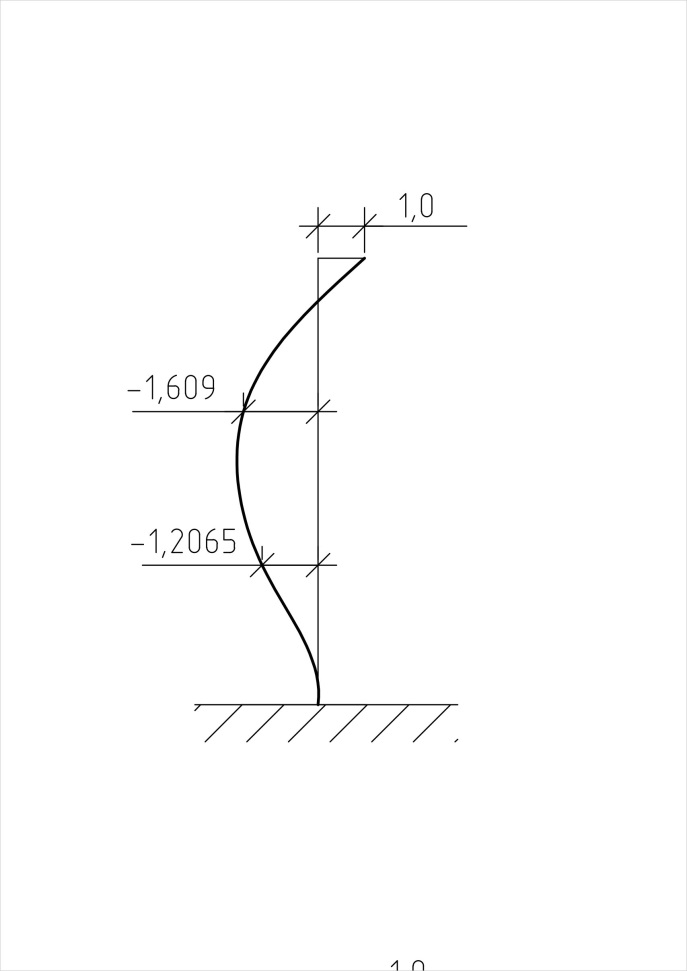
3 форма собственных колебаний
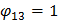
4. 4. 7. Определение форм для II загружения
Относительно ОХ и ОУ:
1 форма собственных колебаний
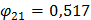
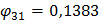
2 форма собственных колебаний
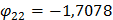
3 форма собственных колебаний
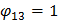
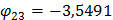
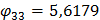
4. 4. 8. Сводим результаты в таблицу
Табл. 2 – Определение коэффициента формы
| Загруж. | Коэффициент формы | номер формы | |||||
| относит. OX | относит. OY | ||||||
|
I | 0, 5175 | 0, 1386 | 0, 5175 | 0, 1385 | |||
| -1, 609 | -1, 2065 | -1, 609 | -1, 2065 | ||||
| -3, 3504 | 5, 2967 | -3, 3504 | 5, 2967 | ||||
|
II | 0, 517 | 0, 1383 | 0, 517 | 0, 1383 | |||
| -1, 7078 | -1, 2673 | -1, 7078 | 1, 2673 | ||||
| -3, 5491 | 5, 6179 | -3, 5491 | -5, 6178 | ||||
4. 5. Определение сейсмических нагрузок на здание
Расчетное значение горизонтальной сейсмической нагрузки определяется по ф. 1 СП14. 13330. 2014 «Строительство в сейсмических районах»
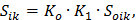
| (9) |
Где: 
– коэффициент, учитывающий назначения сооружения и его ответственность;
– коэффициент, учитывающий допускаемые повреждения зданий и сооружений для ж/б каркаса с диафрагмами и связями;
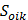– значение сейсмической нагрузки для i - формы собственных колебаний, определяемое в предположении упруго деформированных конструкциях, где k–номер изучаемой массы.
|
|
|
| (10) |
– масса, сосредоточенная в перекрытии с номером k;
– ускорение свободного падения;
– коэффициент, зависящий от расчетной сейсмичности, при 8б A=0, 2;
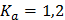– коэффициент, зависящий от расчетной сейсмичности;
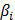– коэффициент динамичности, соответствующий i -форме собственных колебаний, зависящий от периода i-формы колебаний:
Для грунтов 1 и 2 категории:
При 
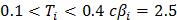
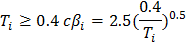
Результаты сводим в табл. 3
Табл. 3 – К определению к. динамичности
| № загруж. | Относит. OY | Относит. OX |
| I | 1, 5049 | 2, 5 |
| 2, 5 | 1, 0375 | |
| 1, 094 | 1, 0139 | |
| II | 1, 2865 | 2, 5 |
| 2, 5 | 1, 0504 | |
| 1, 126 | 1, 0187 |
– коэффициент, учитывающий способность здания рассеивать энергию;
– коэффициент, зависящий от формы деформации здания при его собственном колебании по i-форме.
Для зданий, рассчитываемых по консольной схеме:
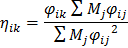
| (11) |
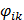– коэффициент формы колебаний;
Результаты сводим в табл. 4.
Табл. 4 – К определению к., зависящего от формы деформаций
| № загруж. | Коэффициент Формы | Номер формы | |||||
| Относит. ОХ | Относит ОУ | ||||||
| I | 1, 286775 | 0, 665906 | 0, 178347 | 1, 286725 | 0, 66588 | 0, 178211 | |
| -0, 3599 | 0, 579071 | 0, 434214 | -0, 3599 | 0, 579071 | 0, 434214 | ||
| 0, 073145 | -0, 24507 | 0, 387428 | 0, 073145 | -0, 24507 | 0, 387428 | ||
| II | 1, 274333 | 0, 65883 | 0, 17624 | 1, 274333 | 0, 65883 | 0, 17624 | |
| -0, 34347 | 0, 586578 | 0, 435279 | 0, 110689 | -0, 18903 | 0, 140276 | ||
| 0, 069159 | -0, 24545 | 0, 388529 | -0, 17934 | 0, 636494 | 1, 007493 | ||
Определяем значения 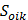, результаты сводим в табл. 5
Табл. 5 – Значение сейсмической нагрузки
| № загруж. | Коэффициент Формы | Номер формы | |||||
| Относит. ОХ | Относит ОУ | ||||||
| I | 682, 542 | 353, 2155 | 94, 60033 | 1133, 777 | 586, 7297 | 157, 0281 | |
| -317, 116 | 510, 2397 | 382, 6005 | -131, 603 | 211, 7495 | 158, 7792 | ||
| 28, 20489 | -94, 4977 | 149, 3929 | 26, 13989 | -87, 5791 | 138, 4552 | ||
| II | 1095, 509 | 535, 2076 | 143, 1706 | 2128, 856 | 1040, 046 | 278, 2174 | |
| -573, 788 | 925, 9861 | 687, 1427 | 77, 69299 | -125, 382 | 93, 04157 | ||
| 52, 03686 | -174, 52 | 276, 2491 | -122, 086 | 409, 4499 | 648, 1101 | ||
|
|
|
