Случайный процесс как модель сигнала

Все эти модели детерминированных сигналов являются известными функциями времени, их использование позволяет успешно решать задачи связанные с определением реакций конкретных систем на заданные входные сигналы.

Случайные составляющие, всегда имеющие место в реальном входном сигнале, всегда считают пренебрежительно малыми и не принимают во внимание.

Однако единственная, точно определённая во времени функция может служить математической моделью сигнала при передаче и преобразовании информации. Поскольку получение информации связано с устранением априорной неопределённости исходных состояний, однозначная функция времени только тогда будет нести информацию, когда она с определённой вероятностью выбрана из множества возможных функций.

Поэтому в качестве моделей сигнала используют случайный процесс.

Каждая выбранная детерминированная функция рассматривается как реализация этого случайного процесса.

Необходимость применения статистических методов исследования диктуется и тем, что в большинстве практически важных случаев пренебрежение воздействием помехи в процессах передачи и преобразовании информации недопустима.

Считается, что воздействие помехи на полезный сигнал проявляется в непредсказуемом искажении его формы.

Математическая модель помехи представлена также в виде случайного процесса, характеризующегося параметрами, определёнными на основе экспериментальных исследований.

Вероятные свойства помехи, как правило, отличны от свойств полезного сигнала, что и лежит основе методов из разделения.

Фундаментальные выводы теории информации базируются на статистическом подходе при описании сигналов и помех. Основными характеристиками случайного процесса как модели сигнала являются следствие:

Под случайным стохастическим процессом подразумевают такую случайную функцию времени U(t), значение которой в каждый момент t случайно.

Конкретный вид случайного процесса зарегистрирован в определённом опыте называемый реализации случайного процесса.

Точно предсказать, какой будет реализация в очередном опыте, практически невозможно. Могут быть определены лишь статистические данные, характеризующие все множество возможных реализаций, называемые ансамблем.

Ценность таких моделей сигналов в том, что появление возможно судить о поведении информационной системы не по отношению к конкретной реализации, а по отношению ко всему ансамблю возможных реализаций.

Основными признаками, по которым классифицируют случайные процессы, являются:

1) Пространство состояний

2) Временный параметр

3) Статистические зависимости между случайными величинами в разные моменты времени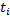

Пространством состояний называемых множество возможных значений величины

Случайный процесс,у которого множество состояний составляет континуум, а изменения состояний возможны только в любые моменты t называется непрерывным случайным процессом.

Если изменения состояний допускаются лишь в конечном или счётном числе моментов времени, то говорят о непрерывной случайной последовательности.

Случайны процесс с конечным множеством состояний, которые могут измениться в произвольные моменты времени, называется дискретнымслучайным процессом.

Если же изменения состояний возможны только в конечном или счетном числе моментов времени, то говорят о дискретных случайных последовательностях.

Примеры реализации указанных случайных процессов представлены на рис.3

Так как в современных информационных системах предпочтение отдается цифровым методам передачи и приобретения информации, то непрерывные сигналы с датчиков, как правило, преобразуются в дискретные, которые описывают дискретными случайными последовательностями.

Среди случайных процессов с дискретным множеством состояний интерес представляют такие, у которых статистические зависимости распространяются на ограниченное число k следующих друг за другом значений. Они называются обобщенными Марковскими процессами k порядка.