Энтропия как мера неопределённости выбора

Фактор получения информации всегда связан с неопределенностью. Необходимо установить количественную меру неопределенности. Рассмотрим источник информации, который может в каждый момент времени случайным образом принять одно из конечного множества возможных состояний.

Такой источник называется дискретным источником. Принято говорить, что различные состояния реализуются вследствие выбора их источником. Каждому состоянию источника можно поставить в соответствия условные обозначения в виде знака (в частности, буквы) из алфавита данного источника

Поскольку одни состояния выбираемы источником чаще, а другие реже, то в общем случае источник характеризуется ансамблем U, то есть полной совокупностью состояний с вероятностью их появления, составляющими в сумме 1. Аналогично ряду распределения дискретной случайно величине.

Опираясь на эти сведения, выведем меру неопределенности выбора состояний источника. Ее же можно рассматривать и как меру количества информации, получаемой при полном устранении неопределённости относительно состояний источника.

Эта мера должна удовлетворять ряду интуитивных требований, к числу которых относятся следующие:

Она должна монотонно возрастать с увеличением возможности выбора, то есть числа возможных состояний источника N, причем недопустимые состояния (состояний с вероятностями, равными 0) не должны учитываться, так как они не меняют неопределенности.

Ограничиваясь, только этим условием за меру неопределенности можно было бы взять число состояний, предположив, что они равновероятны. Однако такая мера противоречит некоторым интуитивным представления, например, при N=1 когда неопределенность отсутствует, она давала бы значение равное 1. Кроме того такая мера не отвечает требованию аддитивности, состоящему в следующем: если 2 независимых источника с числом равновероятностных состояний N и М рассматривать как 1 источник, одновременно реализующий пары состояний (), то естественно предположить, что неопределенность объединённого источника равно N М, то искомая функция должна удовлетворять условию:

Это соотношение (2) выполняется, если в качестве меры неопределённости источника с равновероятными состояниями и характеризующего его ансамбля U принять логарифм числа состояний (3)

Тогда при N=1 H(U)=0 и требование аддитивности выполнятся.

Указанная мера неопределенности (3) была предложена американским ученым Хартли в 1928г.

Основание логарифма не имеет принципиального значения и определяет только масштаб или единицу неопределенности, так как современная информационная техника базируется на элементах имеющих 2 устойчивых состояний, то обычно выбирают основание логарифма = 2. При этом единица неопределённости называется двоичной единицей или битом и представляет собой неопределённость выбора из двух равновероятностных событий «0» или «1», «да» или «нет».

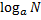
Если основание a=e, то неопределенность измеряется в натуральных единицах – натах.

Если a=10, то неопределённость измеряется в десятичных единицах на 1 состояний – дитах.

Определить меньшее число взвешиваний, которое необходимо произвести на равноплечих весах, чтобы среди 27 внешне неотличимых монет найти 1 фальшивую более легкую.

Общая неопределенность ансамбля U в соответствии с формулой составляет в данном случае двоичных единиц.

Одно взвешивание способно прояснить неопределенность U’, насчитывая 3 возможных исхода (левая чаша весов легче, правая чаша легче, весы находятся в равновесии). Эта неопределенность по той же самой формуле рассчитывается так как

Следовательно, для того, чтобы определить фальшивые монеты достаточно произвести 3 взвешивания.