 |
Взаимосвязь меры Шеннона и меры Хартли
|
|
|
|
Если в источнике может быть реализовано N различных состояний, то вероятность каждого из них 
и неопределенность по Хартли, приходящаяся на каждое состояние выражается числом 
.
Будем считать вероятности событий различными, а неопределенность, приходящаяся на одно конкретное состояние источника, характеризовать по аналогии величиной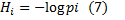 
Это частная неопределенность, представляет собой случайную величину, зависящую от того, какое состояниек источника в действительности реализуется. Усреднив по всему ансамблю ν состояний источника, найдем неопределенность, приходящую в среднем на одно состояние:
Следовательно мера Шеннона является обобщением меры Хартли на случай ансамбля с не равновероятными состояниями. Она позволяет учесть статистические свойства источника информации.
Пример: Сравнить неопределённость, приходящуюся на букву из источника информации ν (алфавита русского языка), характеризуемого ансамблем, представленным в таблице с неопределенностью, которая была бы у того же источника при равновероятном использовании букв.
При одинаковой вероятности появления всех 32 букв алфавита, неопределенность приходится на 1 букву состояния:
| Буква | Вероятность | Буква | Вероятность | Буква | Вероятность | Буква | Вероятность |
| А | 0,064 | Й | 0,010 | Т | 0,056 | Ь(Ъ) | 0,015 |
| Б | 0,015 | К | 0,029 | У | 0,021 | Ы | 0,016 |
| В | 0,039 | Л | 0,036 | Ф | 0,020 | Э | 0,003 |
| Г | 0,014 | М | 0,026 | Х | 0,009 | Ю | 0,007 |
| Д | 0,026 | Н | 0,056 | Ц | 0,004 | Я | 0,019 |
| Е(Ё) | 0,074 | О | 0,096 | Ч | 0,013 | - | 0,143 |
| Ж | 0,068 | П | 0,024 | Ш | 0,006 | 32 знака | |
| З | 0,015 | Р | 0,041 | Щ | 0,003 | ||
| И | 0,064 | С | 0,047 |
Энтропию источника характеризуемого заданным алфавитом найдем, используя формулу:
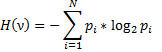
Таким образом, неравномерность распределения вероятностей используемых букв снижает энтропию источника с 5 до 4,42 дв. Ед.
|
|
|
Свойства Энтропии
Рассмотрим основные свойства энтропии, считая, что сформулированные выше условия (1-3) ждя меры неопределенности выполняются.
1) Энтропия является вещественной и неотрицательной величиной, так как
, следовательно 
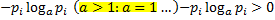
2) Энтропия – величина ограничена для слагаемых 
в диапазоне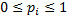 
ограниченность очевидна. Остается определить предел к которому стремится при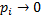 
поскольку 
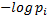неограниченно возрастает, найдем предел:
Воспользуемся правилом Лопиталя
=0
3) Энтропия обращается в 0 лишь в том случае, если вероятность 1 из состояний =1, тогда вероятности всех остальных состояний естественно = 0. Это положение соответсвует случаю, когда состояние источника полностью определено.
4) Энтропия максимальна, когда все состояния источника равновероятны, что легко доказываются методом неопределенных множителей Лагранжа
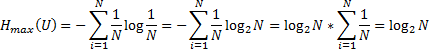
5) Энтропия источника u с двумя состояниями 
изменяющимися от 0 до 1, достигают максимума при равествен вероятностей этих состояний:
График зависимости H(ν) функции p имеет вид 
При p<<(1-p), то есть 
, частная неопределенность прихоидтся на состояние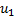 
велика, однако, такие состояния источника весьма редки.
Состояние 
реализуется часто, но неопределенность такого состояния очень мала, поэтому энтропия, характеризующая среднюю неопределенность на одно состояние ансамбля, также мала. Аналогичная ситуация наблюдается при 
то есть при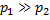 
Энтропия непрерывно зависит от вероятностей отдельных состояний, что непосредственно вытекает из неопределенности функций 
6) Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропий отдельных исходных источников. Не теряя общности, ограничимся рассмотрением объединенных u и v характеристик вероятностей всех возможных комбинаций состояний этих источников
|
|
|
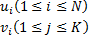
Под объединением двух источников u и v понимают обобщенный источник информации (u,v), характеризуемый вероятностями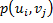 
всех возможных комбинаций состояний источника u и 
источника v. Аналогично трактуется и объединение ансамблей.
|
| 
| 
| … |
| … | 
| 
|
|
| 
| 
| … | 
| … | 
| 
| |
|
| 
| 
| … | 
| 
| 
| ||
| … | … | … | … | … | … | … | … | |
|
| 
| 
| … | 
| … | 
| 
| |
| … | … | … | … | … | … | … | … | |
| 
| 
| … | 
| … | 
| 
| |
| 
| 
| … |
| … | 
| 
|
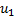
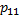
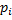
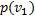
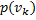
В соответствии с определением 8 энтропии объединения
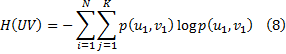
Где 
– вероятности совместной реализации состояний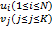 
В случае статистической независимости источников информации u и v запишем
, тогда
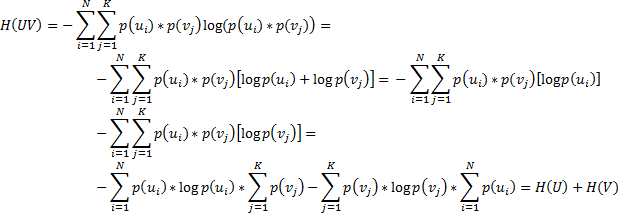
Соответственно для энтропии объединённых нескольких независимых источников u,v,z…w
В дальнейшем для придания общности полученного результата о неопределенности выбора будем говорить в основном применительно к математическим моделям источников информации в виде ансамблей.
7) Энтропия характеризует среднюю неопределенность выбора одного состояния из ансамбля состояний. При ее определении используют только вероятности состояний, полнностью игнорируя их содержательную сторону. Поэтому энтропия не может служить средством решения любых задач, связанных с неопределенностью. Например, при использовании энтропии для оценки неопределенности действия лекарства, приводящего к полному выздоровлению 90% и к улучшению 10%, она получит такую же как у лекарства, вызывавшую в 90% случаев значительное ухудшение состояния, а в 10% - незначительное ухудшения состояния.
8) Энтропия как мера неопределенности согласуется с экспериментальными данными, полученными при изучении психологических реакций человека, в частности, реакции выбора.
Установлено, что время безошибочной реакции на последовательность беспорядочно чередующихся равновероятных раздражителей (например, загорающихся лампочек) растет с увеличением их числа. Это время характеризует неопределенность выбора одного раздражителя. Замена равновероятных раздражителей неравномерно приводит к снижению среднего времени реакции равно на столько, на сколько уменьшается энтропия.
Пример: заданы ансамбли U V, 2 дискретные случайные величины U’ и V’
Сравнить их энтропии, для источников с N равновероятных состояний характеризует ансамблем энтропия U 
Так как вероятность всех состояний одинакова, то вероятность одного состояния 
|
|
|
Тогда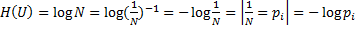 
Так как энтропия не зависит от конкретных значений случайно величины, а зависит только вероятность появления этих значений, то для данного примера эти энтропии одинаковы, поскольку каждая из случайных величин имеет одинаковые вероятности для разных значений, и число этих значений также одинаково.
Для U’ V’ N=4 
|
|
|
