 |
Если на начало экстраполяционного периода (год t) численность населения
|
|
|
|
S(t)= 100 000 000 человек, и предполагается, что население будет увеличиваться на 1% в год, то через год численность населения будет равна:
S(t+1)= 100 000 000×(100+1)/100=
=100 000 000×1,01=101 000 000
через два год численность населения будет равна:
S(t+1)= 101 000 000×1,01=102 010 000
Условный пример роста населения, изначальная численность которого 100000000
| Год (t) | Числ-ть насел. S(t) | Темп роста |
| 1,01 | ||
| 1,01 | ||
| 1,01 | ||
| 1,01 | ||
| 1,01 | ||
| 1,01 | ||
| 1,01 | ||
| 1,01 | ||
| 1,01 | ||
| 1,01 | ||
| 1,01 | ||
Если население увеличивается на 1% в год, то через два года оно вырастет не на 2%, а на 2,01%, через 3 года не на 3%, а на 3,03%, через 10 лет не на 10%, а на 10,46%. В данном случае, так же, как и в отношении денежного вклада в банке, действует правило сложных процентов.
Однако сами темпы прироста населения никогда НЕ ОСТАЮТСЯ ПОСТОЯННЫМИ. Со временем они изменяются по величине и даже по знаку, то есть прирост населения сменяется убылью населения.
По методу экстраполяции составлены прогнозы английского демографа Томаса Роберта Мальтуса (Thomas Robert Malthus, 1766-1834). Он считал, что численность населения увеличивается в два раза за каждые 25 лет.
Кроме того, при применении экстраполяционного метода прогнозируется только общая численность населения, а не его состав по полу и возрасту, который очень важен с социально-экономической точки зрения. Поэтому гораздо чаще используется метод компонент.
Метод компонент или метод ПЕРЕДВИЖКИ ВОЗРАСТОВ - предназначен как для составления краткосрочных демографических прогнозов, не более чем на 10 лет, так и для среднесрочных (на 10-30 лет) и долгосрочных (на 30 лет и более). Прогнозируется не только общая численность населения, но также и его состав по полу и возрасту.
|
|
|
Об алгоритме метода компонент или
ПЕРЕДВИЖКИ ВОЗРАСТОВ.
Существует еще один показатель таблиц смертности – СРЕДНЕЕ ЧИСЛО ЖИВУЩИХ в возрасте x, то есть, L(x) – не путать с ЧИСЛОМ ДОЖИВАЮЩИХ до возраста x, то есть, l(x).
Во всех возрастах старше одного года L(x) рассчитывается по формуле:
x ≥ 1
L(x)= 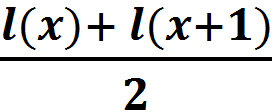
В возрасте до 1 года
x=0
L(0) = l(0)×a(0)+ l(1)×(1-a(0))
Где a(0) – это средний возраст детей, умерших на первом году жизни (в долях года)
В современных условиях
a(0) ≈0,15.
Т.е. L(0)=l(0)×0,15+ l(1)×0,85)
На основании показателей L(x) определяются
КОЭФФИЦИЕНТЫ ПЕРЕДВИЖКИ ВОЗРАСТОВ
P(x,x+1),
Которые используются для составления демографических прогнозов.
P(x,x+1) = 
Не следует смешивать или путать показатели
P(x,x+1)
И p(x), который тоже входит в таблицы смертности.
P(x) – это вероятность дожить от точного
возраста x до точного возраста x+1
p(x)=1-q(x) = 
Вероятности смерти q(x) и дожития p(x) – это вероятности умереть или дожить от одного дня рождения до другого дня рождения.
Но по данным переписи или оценки численности населения в возрасте x лет на начало года t S(x,t) – это не численность тех людей, которым только что исполнилось x лет (т.е. у которых день рождения). S(x,t) – это численность лиц, возраст которых составляет от ровно x лет до x лет 11 месяцев и 29 дней – в среднем же им по x+0,5 лет
В таблице смертности показателю S(x,t) соответствует не l(x), а L(x)
P(x,x+1) можно рассматривать как вероятность дожить от возраста x+0,5 до возраста x+1,5
С помощью коэффициентов передвижки возрастов численность населения в возрасте x лет на начало года t пересчитывается или передвигается с поправкой на смертность в возраст x+1 лет на начало года t+1
S(x,t)× P(x,x+1)= S(x+1,t+1)
Этот расчет делается отдельно для мужчин и женщин.
|
|
|
Для мужчин:
Sm(x,t)× Pm(x,x+1)= Sm(x+1,t+1)
Значок (индекс) m означает male – мужской пол
Для женщин:
Sf(x,t)× Pf(x,x+1)= Sf(x+1,t+1)
Значок (индекс) f означает female – женский пол
Прогнозируемое число родившихся определяется отдельно для каждого возраста женщин по формуле:
N(x,t)= 
Где
Sf(x,t) – численность женского населения в возрасте x лет на начало года t.
Sf(x,t+1) – численность женского населения в возрасте x лет на начало года t+1
|
|
|


