 |
Изучение динамики качественных показателей по нескольким единицам (территориям, предприятиям, странам)
|
|
|
|
Изменение себестоимости продукции А по фирме определяется индексом: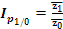 
, где 
, 
- средняя себестоимость единицы продукции по группе предприятий.
Средняя себестоимость единицы продукции исчисляется по формуле средней арифметической взвешенной: 
; 
.
Следовательно, 
: 
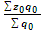- этот индекс называется индексом переменного состава, т.е. исчисление средней с меняющимися (переменными) весами.
Величины 
и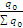 
отражают распределение продукции по предприятиям, поэтому формула индекса себестоимости переменного состава может быть записана в виде: 
..
= – = 
– 
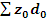- абсолютное изменение средней себестоимости по группе предприятий.
Чтобы устранить влияние изменений в структуре весов на показатель изменения уровня себестоимости, рассчитывается отношение средних с одними и теми же весами: 
= 
: 
= 
= 
- этот индекс отражает изменение уровня средней себестоимости в связи с изменением значений себестоимости по отдельным предприятиям:
= 
- абсолютное изменение средней себестоимости за счет изменения уровня себестоимости по предприятиям.
Индекс влияния структурных сдвигов в объеме продукции определяется по формуле: 
= 
= 
- абсолютное изменение средней себестоимости за счет структурных сдвигов в объеме выпуска продукции.
Поскольку изменение 
в целом по группе предприятий определяется изменением двух факторов, то 
= 
· 
. = + 
= – .
Использование индексного метода в анализе
Взаимосвязи экономических явлений
Индексный метод используется при изучении роли отдельных факторов в динамике какого-либо сложного явления, позволяя определить размер абсолютного и относительного изменения сложного явления за счет каждого фактора в отдельности.
|
|
|
Предположим сложный показатель: А= а·в (а,в – показатели-факторы). Изменение сложного явления можно представить индексом:
= 
= 
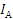Абсолютное изменение явления А под влиянием всех факторов представляет собой разность между числителем и знаменателем индекса:
= 
– 
= 
– 
.
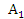Для выявления влияния каждого фактора в отдельности индекс сложного показателя раскладывают на частные (факторные) индексы, характеризующие роль каждого фактора.
Применяется два метода разложения общего индекса на частные:
1) метод обособленного изучения факторов;
2) метод последовательно-цепной.
Агрегатный индекс общей стоимости продукции
= 
· 
= 
Общее абсолютное изменение общей стоимости продукции за счет двух факторов: 
.
Абсолютное изменение общей стоимости продукции за счет отдельных факторов:
а) изменение физического объема продукции: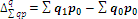 
.
б)среднее изменение цен на продукцию: 
Общее абсолютное изменение результативного показателя составит алгебраическую сумму абсолютных изменений за счет отдельных факторов, т.е.: 
.
Доля каждого фактора в общем абсолютном изменении результативного показателя определяют следующим образом:
а) физического объема продукции: 
.
б) среднего изменения цен на продукцию:: 
.
Агрегатный индекс общих затрат 
= · 
= 
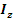Абсолютное изменение общих затрат на выпуск продукции за счет отдельных факторов:
а) изменение физического объема продукции: 
.
б)среднее изменение себестоимости единицы продукции: 
Общее абсолютное изменение общих затрат составит
.
Агрегатный индекс общих затрат рабочего времени на выпуск продукции 
= · 
= 
.
Выявление влияния отдельных факторов на абсолютное изменение общего объема затрат рабочего времени выполняется аналогично предыдущим:
а) изменение физического объема продукции: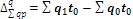 
.
б)изменение затрат рабочего времени: 
Общее абсолютное изменение: 
.
Задача.
Выпуск продукции по заводу за два квартала:
|
|
|
Определить:
1) изменение цен (%) по каждому виду продукции и среднее изменение цен по всему ассортименту продукции;
2) изменение (%) выпуска каждого вида продукции, а также изменение выпуска продукции в целом по предприятию;
3) абсолютное изменение общей стоимости продукции, выделив из общей суммы изменение за счет количества продукции и за счет цен.
Решение.
1) для характеристики изменения цен по каждому виду продукции используем индивидуальные индексы цен: 
:
1. плуги навесные: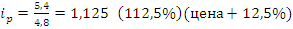 
2. плуги прицепные 
3. культиваторы: 
Среднее изменение цен: 
= 
Т.о. цены в среднем повысились на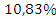 
, за счет чего стоимость продукции повысилась на 
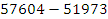= 5631 тыс.руб.
2) Для характеристики изменения выпуска продукции каждого вида найдем индивидуальные индексы: 
:
1. 
2. 
3. 
.
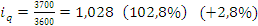Для характеристики изменения выпуска продукции в целом по предприятию вычисляется агрегатный индекс физического объема:
= 
= 
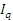Стоимость продукции увеличилась на 
руб.
3) = 
= 
– 
= 673 тыс. руб– абсолютное изменение стоимости за счет изменения выпуска продукции
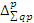= 5631 тыс.руб – абс. изменение стоимости за счет изменения цен
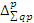= + = 673 + 5631 = 6304 тыс.руб. и соответствует раннее полученной сумме.
Доля каждого фактора:
а) физического объема продукции: 
= 
(10,68%)
б) среднего изменения цен: 
= 
(
%).
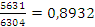Выборочное наблюдение
В целом ряде случаев средние и относительные величины для какой-либо совокупности рассчитываются на основе данных выборочного наблюдения, суть которого заключается в том, что из генеральной совокупности, наудачу, часто случайно, отбирается 𝑛 единиц, составляющих выборочную совокупность; для отобранных единиц рассчитываются обобщенные характеристики (средние или относительные показатели), а затем результаты выборочного обследования распространяются на всю генеральную совокупность. Основной задачей при этом является определение ошибок выборки.
Различают среднюю и предельную ошибки выборки.
Средняя ошибка выборки (𝜇) характеризует среднюю величину возможных расхождений выборочной и генеральной средней (или доли).
При случайном повторном отборе средняя ошибка выборочной средней определяется по формуле 𝜇 = 
, где 
- дисперсия изучаемого показателя в генеральной совокупности, а 𝑛 – объем выборки.
|
|
|
Средняя ошибка выборочной доли определяется по формуле 𝜇 = 
, где 𝑤 – выборочная доля единиц, обладающих изучаемым признаком, а 
- дисперсия доли (альтернативного признака).
При бесповторном отборе в формулах под знаком радикала появляется множитель 
, где 𝑁- численность генеральной совокупности.
Предельная ошибка выборки, обозначаемая через ∆, рассчитывается как ∆ = 𝑡𝜇, где 𝜇 – средняя ошибка выборки, 𝑡 – коэффициент доверия, показатель, определяющий размер ошибки в зависимости от того, с какой вероятностью 𝑷 она находится.
Значения 𝑡 и 𝑷 (вероятность допуска той или иной ошибки) даны в специальных таблицах, где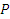 
рассматривается как функция 𝑡 и рассчитывается по формуле: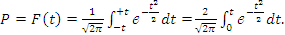 
Таким образом, общая формула предельной ошибки выборки ∆ = 𝑡𝜇 для средней приобретает вид ∆ = 𝑡 (для повторного отбора) или
∆ = 𝑡 
(для бесповторного отбора), а для доли соответственно
∆ = 𝑡 и ∆ = 𝑡 
.
Формулы предельной ошибки несколько конкретизируются и в зависимости от применяемого вида выборки. Так, указанные выше формулы применимы для собственно случайной и механической выборок.
Для типической ∆ = 𝑡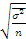 
или ∆ = 𝑡 
.
В этом случае ошибка выборки зависит от внутригрупповой вариации.
При серийной (гнездовой) выборке, ∆ = 𝑡 
.
Все рассмотренные выше формулы используются при так называемой большой выборке.
Если 𝑛 < 20, то выборка именуется малой и при расчете ошибок выборки необходимо учитывать следующие моменты:
1) в формуле средней ошибки в знаменателе принимается 𝑛 – 1, т.е.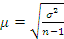 
2) при определении доверительных интервалов исследуемого показателя в генеральной совокупности пользуются таблицами вероятности Стьюдента, где 𝑃= 𝑆(𝑡,𝑛) определяется в зависимости от объема выборки и 𝑡.
Рассмотрим решение некоторых задач к этой теме с применением формул предельной ошибки выборки.
Задача 1.
Методом собственно случайной выборки обследована жирность молока у 100 коров. По данным выборки средняя жирность молока оказалась равной 3,64%, а дисперсия составила 2,56.
|
|
|
Определить:
1) среднюю ошибку выборки;
2) с вероятностью, равной 0,954, предельные значения генеральной средней.
Решение.
1) формула средней ошибки выборки: 𝜇 = . По условию 𝑛 = 100, = 2,56. Отсюда 𝜇 = 
2) формула предельной ошибки выборки: ∆ = 𝑡𝜇. По таблице значений 𝐹(𝑡) при 𝑃 = 0,954 находим, что 𝑡 = 2. Отсюда ∆ = 2·0,16 = 0,32, или 
= 
3,64 
0,32, т.е. предельные значения жирности молока (или доверительный интервал генеральной средней) определятся как
3,32% ≤ ≤ 3,96%.
Задача 2.
Для определения средней заработной платы рабочих завода была произведена 20% бесповторная выборка (по цехам) с отбором единиц пропорционально численности групп. Результаты выборки представлены в приводимой ниже таблице:
| цех | Объем выборки, чел., 𝑛 | Средняя заработная
плата, руб., 
| Среднее квадратическое
отклонение, руб., 
|
| Всего | – | – |
С вероятностью 0,997 (т.е. 𝑡 = 3) определить пределы, в которых находится средняя заработная плата всех рабочих завода.
Решение.
1) Находим общую выборочную среднюю заработную плату:
(руб)
2) Находим среднюю из групповых дисперсий:
= 
= 
3) Определяем предельную ошибку выборочной средней заработной платы. Для типической бесповторной выборки
∆ = 𝑡 
= 3 
= 
Отсюда генеральная средняя
= 
= 888,4 7,9 или 880,5 ≤ ≤ 896,3, т.е. средняя заработная плата всех рабочих находится в пределах от 880,5 до 896,3 руб.
|
|
|
