 |
Корреляционно-регрессионный анализ
|
|
|
|
При исследовании социально-экономических явлений часто приходится иметь дело со взаимосвязанными показателями. Изучить, насколько изменение одного показателя зависит от изменения другого (или нескольких), - одна из важнейших задач статистики.
Следует различать функциональные и корреляционные связи.
Основными задачами при изучении корреляционных зависимостей являются: 1) отыскание математической формулы, которая бы выражала эту зависимость y от x; 2) измерение тесноты такой зависимости.
Возможны различные формы связи: 
1) прямолинейная:  =
= 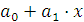 ;
;
2) криволинейная в виде:
а)  =
= 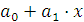 +
+  (или высших порядков);
(или высших порядков);
б) гиперболы:  =
= 
в) показательной функции:  =
=  и т.д.
и т.д.
Параметры для всех уравнений связи чаще всего определяют из так называемой системы нормальных уравнений, отвечающих требованию «метода наименьших квадратов» (МНК). Это требование можно записать как 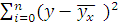 → min или, при линейной зависимости,
→ min или, при линейной зависимости,  =
= 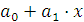 ,
, 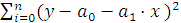 → min. Найдя частные производные указанной суммы по
→ min. Найдя частные производные указанной суммы по 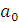 и
и  и приравняв их к нулю, получим систему уравнений, решение которой и дает параметры искомого уравнения регрессии:
и приравняв их к нулю, получим систему уравнений, решение которой и дает параметры искомого уравнения регрессии: 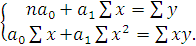
Если связь выражена параболой второго порядка  =
= 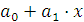 +
+  , то система нормальных уравнений для отыскания параметров
, то система нормальных уравнений для отыскания параметров 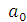
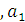 , и
, и 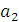 , выглядит следующим образом:
, выглядит следующим образом: 
Вторая задача - измерение тесноты зависимости – для всех форм связи может быть решена с помощью исчисления теоретического корреляционного отношения (η): 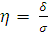 =
= 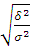 .
.
Линейный коэффициент корреляции можно выразить и другими формулами: 𝑟 =  ; 𝑟 =
; 𝑟 = 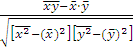 или 𝑟 =
или 𝑟 =  .
.
Линейный коэффициент корреляции может принимать по модулю значения от 0 до 1 (знак «+» при прямой зависимости и знак «–» при обратной зависимости).
Задача 1.
Пусть по 10 однотипным предприятиям имеются следующие данные о выпуске продукции (𝑥) в тыс. ед. и о расходе условного топлива (𝑦) в тоннах (графы 1 и 2 таблицы).
|
|
|
Требуется найти уравнение зависимости расхода топлива от выпуска продукции и измерить тесноту зависимости между ними.
Решение.
| 𝑥 | 𝑦 | 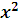
| 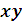
|  =1,16+0,547 =1,16+0,547 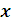
| 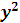
|
| 3,9 4,4 5,5 5,5 6,6 6,6 8,8 12,1 12,1 14,3 | |||||
1) Рассматривая уравнение регрессии в форме линейной функции вида  =
= 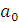 +
+ 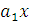 , параметры данного уравнения найдем из системы нормальных уравнений
, параметры данного уравнения найдем из системы нормальных уравнений 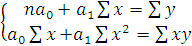 , а необходимые для решения суммы рассчитаны выше в таблице. Подставляем их в уравнение и решаем систему:
, а необходимые для решения суммы рассчитаны выше в таблице. Подставляем их в уравнение и решаем систему: 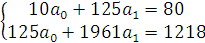 ,
, 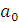 = 1,16 и
= 1,16 и 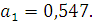
Отсюда 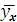 =1,16 + 0,547
=1,16 + 0,547 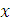 .
.
Подставляя в это уравнение последовательно значения 𝑥 = 5, 6, 8, 10 и т.д., получаем выравненные (теоретические) значения результативного показателя  (графа 5 таблицы).
(графа 5 таблицы).
Поскольку параметры уравнения регрессии являются оценочными, то для каждого из них рассчитывается средняя ошибка, т.е. 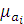 .
.
Конкретный расчет ошибок для 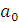 и
и  по данным нашего примера приведен далее.
по данным нашего примера приведен далее.
2) Для измерения тесноты зависимости между 𝑦 по 𝑥 воспользуемся прежде всего линейным коэффициентом корреляции:
находим 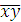 = 121,8;
= 121,8; 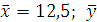 = 8;
= 8; 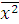 = 196,1,
= 196,1, 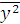 = 77,
= 77,
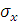 =
= 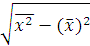 =
= 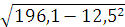 =
= 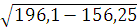 =
= 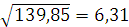
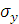 =
=  =
= 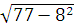 =
= 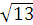
 .
.
Отсюда по формуле 𝑟 = 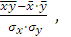 𝑟 =
𝑟 = 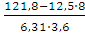 =
= 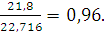
- характеризует не только меру тесноты зависимости вариации 𝑦 от вариации 𝑥, но и степень близости этой зависимости к линейной;
При расчете коэффициента корреляции, особенно если он исчислен для небольшого числа наблюдений (𝑛), очень важно оценить его надежность (значимость). Для этого рассчитывается средняя ошибка коэффициента корреляции ( 
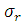 =
= 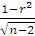 , где (
, где (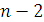 ) – число степеней свободы при линейной зависимости.
) – число степеней свободы при линейной зависимости.
А затем находится отношение коэффициента корреляции к его средней ошибке, т.е. 𝑡 =  , которое сравнивается с табличным значением 𝑡 –критерия Стьюдента.
, которое сравнивается с табличным значением 𝑡 –критерия Стьюдента.
В рассматриваемом примере средняя ошибка коэффициента корреляции: 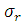 =
= 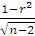 =
= 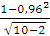 =
=  =
= 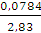 = 0,028, 𝑡 =
= 0,028, 𝑡 =  =
= 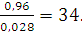
|
|
|
По таблице приложения находим, что при числе степеней свободы
𝑘 = 10 – 2 = 8 и уровне значимости α = 0,05 табличное 𝑡 равно 2,306, т.е. 𝑡табл = 2,306.
Поскольку фактическое (расчетное) 𝑡 больше табличного, т.е. 𝑡факт > 𝑡табл , то линейный коэффициент корреляции 𝑟 = 0,96 считается значимым, а связь между 𝑥 и 𝑦 - реальной.
|
|
|


