 |
Методы получения магнитных наноточек
|
|
|
|
Метод электрохимического осаждения.
Один из способов формирования магнитной наноструктуры – электрохимическое осаждение - почти полностью повторяет метод получения нанонитей, иллюстрированный на рис. 11.9. Модификация метода для осаждения наноточек изображена на рис. 12.1-12.3 [1]. На рис. 12.1 изображена схема и внешний вид прибора для анодирования алюминия с формированием пористой окиси алюминия. Используется обычная установка для электрохимической полировки. В ряде предлагаемых способов используются пониженные температуры, что обеспечивается охладителем (coolant). Варьируя условия анодизации,
 |
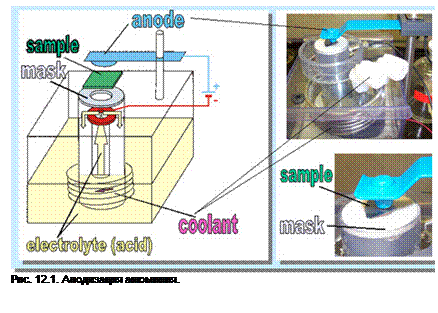состав и свойства электролитов (щавелевая, фосфорная, серная кислоты), время, напряжение (плотность тока) и.т.д., можно получать поры различного размера. Механизм формирования пор схематично изображен на рис. 12.2. В электрохимическом процессе анодизации алюминий превращается в окись алюминия. Процесс идет интенсивнее в области пор, поскольку именно там градиент потенциала выше. Вследствие конкуренции электрических и механических сил, поры имеют тенденцию формирования самоорганизованной гексагональной, плотноупакованной структуры [2,3].
Нанолитография с пористой окисью алюминия.
Схема получения магнитных наноточек изображена на рис.12.3. Описанным выше методом из Al, нанесенного на Si-подложку создается слой Al2O3, играющий роль пористой маски. Через образованные путем анодизации поры в Al2O3 производится осаждение магнитного материала, скажем с помощью испарения. Таким образом можно получить массив магнитных наноточек, покрывающий площадь более 1 cм2. [1,4].
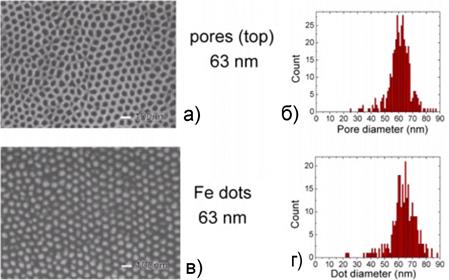
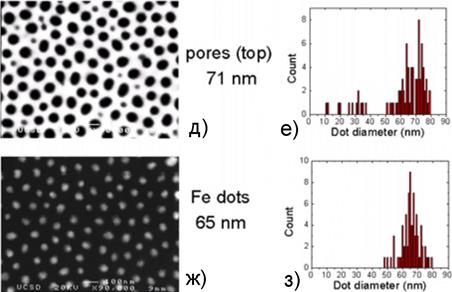
Если вместо кремниевой подложки использовать химически более активный материал, то такую подложку на конечном этапе можно растворить и получить самоподдерживающуюся маску в виде мембраны. Эти мембраны затем можно использовать для нанесения магнитных нанопроволок и наноточек, рис. 12.4. Также можно осадить наноточки через маску непосредственно на кремний. Рис.12.4 демонстрирует достаточно малый разброс диаметров нанопор и наноточек, осаждаемых с помощью такой пористой маски.
|
|
|
|
|
| Рис. 12.4. Осаждение магнитных наноточек либо с помощью самоподдерживающейся маски (а-г), либо через маску на кремнии (д-з). |
Намагниченность наноточек.
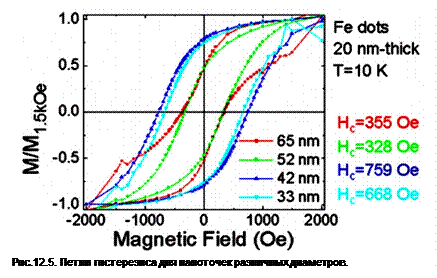Петли гистерезиса, полученные СКВИД-методом, для наноточек различных размеров приведены на рис. 12.5. Толщина (высота) точек была около 20 нм. Диаметр в интервале 33 нм – 65 нм. Видно, что с ростом поперечного размера частиц коэрцитивная сила уменьшается. В диапазоне диаметров от 30 до 100 нм происходит переход от монодоменной структуры к вихревой или вортексной (vortex) микромагнитной структуре. Петли более прямоугольны (M(H=0)/Ms больше) при меньших размерах наноточек за счет антиферромагнитного обменного взаимодействия с собственным окислом на поверхности. Прямое экспериментальное подтверждение существования вихревой структуры получено методом магнитосиловой микроскопии (МСМ, глава VII) [5]). Поскольку МСМ чувствительна к изменению вертикальной составляющей намагниченности Mz, то в МСМ изображениях вихревая структура появляется в виде контраста в центре наноточки, где МСМ детектирует наибольшее изменение поля рассеяния, вызванное вертикальной компонентой Mz, как это видно из рис. 12.6. Латеральное разрешение в МСМ недостаточно для того, чтобы дать информацию о размере ядра вихря. Для этого используются методы спин-поляризованной сканирующей туннельной микроскопии [6] и лорентцевской просвечивающей электронной микроскопии (ЛПЭМ, глава VII) [7].
|
|
|
|
| Рис. 12.6. МСМ изображение наноточек высотой 50 нм и различного диаметра [5]. |
|
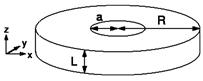
| Рис. 12.7. Геометрия цилиндрической наноточки. |
Теория и численное моделирование микромагнитной структуры наноточек.
Аналитическая модель микромагнитной структуры наноточек, так называемая модель жесткого вихря, была предложена Усовым [8,9]. Согласно этой модели наноточка состоит из двух цилиндрических областей центральной радиусом r<a, и внешней a<r<R, рис. 12.7. Вертикальная компонента намагниченности всюду равна нулю, за исключением центральной области, являющейся ядром вихря. Распределение намагниченности в отсутствие внешнего магнитного поля, Hext = 0, получается, исходя из вариационного принципа минимизации полной энергии (обменная плюс магнитостатическая). В результате получены следующие соотношения. Для r<a:
| 
| (11.1) | |
| 
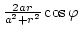
| (11.2) | |
| 
| ||
|  ,
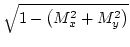
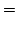
| (11.3) |
где r,φ – полярные координаты.
Для внешней области r > a:
| 
| (11.4) | |
| 
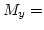
| (11.5) | |
| 
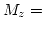
| (11.6) |
Радиус ядра дается выражением
(11.7)
где обменная длина lex имеет вид:
(11.8)
κ – численная константа ([8,9]), L высота наноточки и g = R/L – апексное отношение.
Различный вид lex (11.8) и δ0 = (А/<K>)1/2 в (9.2) обусловлен тем, что анизотропией при рассмотрении микромагнетизма наноточек можно пренебречь. Анизотропия играет большую роль в распределении магнитных моментов для частиц с размерами около и более сотен нанометров [10], на уровне десятков нанометров микромагнитная структура в основном определяется обменным и магнитостатическим взаимодействием. Обменные силы заставляют магнитные моменты ориентироваться параллельно, магнитостатические силы противостоят образованию магнитных полюсов. Чем меньше образец, тем существеннее роль обменных сил, так что в точках размером в десятки нанометров магнитные моменты почти параллельны. При больших размерах точек намагниченность конфигурируется таким образом, чтобы избегать формирования полюсов на поверхности, что приводит к закручиванию магнитных моментов и формированию вихревой структуры.
Для пермаллоя Ni80Fe20 с типичными параметрами Ms = 8x105 А/м, μ0Ms ≈1 Тл, обменная константа А = 13х10-12Дж/м = 1.3х106 эрг/см, получаем lex ≈ 5.7 нм и для R=100 нм и L = 20 нм получаем а ≈ 11 нм.
|
|
|
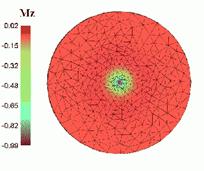
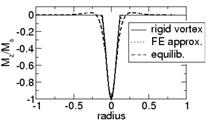
Результаты численного моделирования показаны на рис. 12.8 и 12.9 [11]. На рис. 12.8. изображено распределение Mz, рассчитанное методом конечных элементов, которое показывает присутствие вихревого распределения в центре (латеральное распределение Mx,y вне ядра также имеет вихревую структуру, но оно не показано из-за мелкого масштаба сетки, использованной в расчете). Радиальное распределение Mz, рассчитанное в приближении конечных элементов (FE approx.), на рис. 12.9 сопоставлено с предсказаниями модели жесткого вихря (rigid vortex) и с результатами расчетов релаксации
| 
|
| Рис. 12.8. Распределение Mz по результатам [11] | Рис. 12.9. Радиальное распределение Mz. |
магнитных моментов путем интегрирования уравнений Ландау-Лифшица [11]. Из этого рисунка видно, что имеется качественное и неплохое количественное согласие сопоставляемых методов расчета. Расхождение имеется в оценке диаметра вихря – модель релаксации магнитных моментов дает примерно на 50% больший размер ядра вихря. Помимо этого, эта модель предсказывает положительную составляющую намагниченности в области, прилегающей к ядру до r ≈ 50 нм.
Теоретическая кривая гистерезиса.
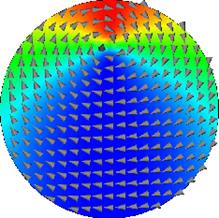
На рис. 12.10 показана теоретическая кривая гистерезиса. Для очень большого внешнего магнитного поля, ориентированного в плоскости наноточки (точка (а)), микромагнитная структура однородна, магнитные моменты ориентируются вдоль поля, рис. 12.11(а). С уменьшением поля (сплошная линия на рис. 12.10) распределение магнитных моментов, под воздействием магнитостатического поля
(а)
|  (b)
|
(c)
| 
(d)
|
| Рис. 12.11. Микромагнитная структура наноточки во внешнем поле Hex, соответствующем точкам (а) – (d). |
рассеяния, становится все более неоднородным. При дальнейшем уменьшении поля микромагнитная симметрия нарушается и развивается предвихревое “C” –состояние. При поле около 5 кА/м формируется вихревая конфигурация на периферии, рис. 12.11(b), но вихрь быстро смещается в центральную область. Средняя намагниченность наноточки резко падает, точка (b) на рис.12.10. Когда Hex = 0, то ядро вихря занимает центр и намагниченность становится также равной нулю, рис. 12.11с (точка С на рис. 12.10). При увеличении поля в отрицательную область ядро вихря выталкивается к периферии и при Hex = -70 кА/м вихрь полностью исчезает (аннигилирует). Возникает второй скачок в петле гистерезиса, точка (d) на рис. 12.10.
|
|
|
Сопоставляя результаты расчетов и экспериментальные результаты можно сделать вывод, что аналитическая модель жесткого вихря хорошо описывает магнитную восприимчивость, распределение намагниченности и поле аннигиляции вихря для невысоких внешних полей в широком интервале диаметров наноточек [14,15,16,17]. Экспериментально наблюдаемое поле зарождения вихря оказывается несколько более высоким, чем предсказываемое моделью жесткого вихря [18]. Это, по-видимому, связано с упрощенной С-формой зарождающегося вихря при реверсировании внешнего поля в круглых наноточках, принятой в этой модели. Исследования показывают, что начальная восприимчивость, поле зарождения и поле аннигиляции вихря зависят от намагниченности насыщения Ms и масштабируются как функции безразмерного параметра L/R [14,15].
Фазовая диаграмма.
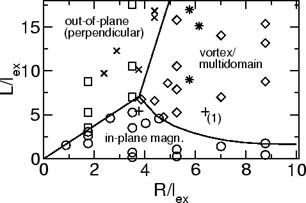
Результаты исследований по микромагнитной структуре наноточек можно обобщить в своего рода фазовой диаграмме, изображенной на рис. 12.12. Открытые символы изображают результаты расчетов методом конечных элементов [11]. Кружки (О) изображают состояния с наинизшей энергией и намагниченностью в плоскости, квадраты (□) – с
|
| Рис.12.12. Фазовая диаграмма намагниченности в функции размеров наноточек, приведенных к обменной длине. |
перпендикуляр-ной намагни-ченностью, ромбики (◊) – с вихревой или мультидоменной структурой. Эксперимен-тальные данные (Ross et al. [12]): (х) – перпендику-лярная намагни-ченность, (+) – продольная (в плоскости) намаг-ниченность, (*) – вихревая/мультидоменная намагниченность. Сплошные линии – аналитическая равновесная однодоменная модель (Metlov et al. [13]). Как видно из диаграммы, переход из намагниченности, ориентированной в плоскости, в вихревую достаточно резкий. Это связано с разрушением одной симметрии
L/R = 1, R = 10 нм
|
L/R = 1, R = 25 нм
|
L/R = 1, R = 28 нм
|
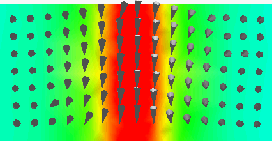
| Рис. 12.13. Равновесное распределение намагниченности в отсутствие внешнего поля в сечении вдоль оси цилиндра. |
(однородной намагниченности) и формированием другой (цилиндрической симметрии). Линия, разделяющая продольную (in-plane) и поперечную (out-of-plane) намагниченности имеет наклон равный 1.8, который находится в соответствии с данными Ross et al. [12] и аналитическими расчетами [19]. Магнитооптические измерения кривой гистерезиса [20] также свидетельствуют о четкой границе между этими двумя режимами. Однодоменные частицы сохраняют высокую остаточную намагниченность и
|
|
|
L/R = 2, R = 10 нм
| 
L/R = 2, R = 25 нм
|
L/R = 2, R = 40 нм
| Рис. 12.14. Распределение намагниченности в наноточке с L/R = 2 в сечении через ось цилиндра. |
переключаются при очень низких полях, в то время как внезапная потеря намагниченности при уменьшении внешнего поля (рис. 12.10) свидетельствует о замыкании магнитного потока, характерного для вихревой конфигурации, рис. 12.13. Однако, переход из вихревого состояния в перпендикулярное намагничивание не очень хорошо определен. Численные эксперименты показывают, что этот переход происходит плавно. С уменьшением размерного отношения L/R появляется нестабильность намагничивания и возникает достаточно неоднородное распределение намагничивания, рис. 12.14. Линия для перехода в состояние перпендикулярной намагниченности на рис. 12.12 проведена из условия Mz/Ms = 0.75. Несмотря на то, что задача не является двумерной (необходимо учитывать компоненту Mz), тем не менее, экспериментальные данные и результаты численного моделирования находятся в хорошем согласии с результатом аналитического расчета [13].
|
|
|
