Наведенная магнитная анизотропия

Подавление магнитокристаллической анизотропии означает, что, с одной стороны, материал становится магнитно-изотропным, с другой – более мягким, поскольку отпадает необходимость преодолевать поле анизотропии.

Н_к = 2К₁/I_s. (9.7)

Однако отсутствие анизотропии не везде полезно. В частности, как мы увидим далее, в переменных магнитных и высокочастотных магнитных полях важно сместить область ферромагнитного резонанса, как можно дальше к высоким частотам. Частота ферромагнитного резонанса

f_FMR= γμ₀(I_sH_k)^1/2, (СИ) (9.8)

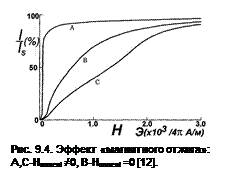
где γ = geħ/(2m) ≈ 2.2 10⁵ м/(А сек) – гиромагнитная постоянная. Таким образом, чем выше H_k, тем лучше высокочастотные свойства материала. Проблема решается созданием наведенной анизотропии в нанокристаллических материалах взамен магнитокристаллической. Наведенная анизотропия возникает при создании в процессе формирования материала определенного выделенного направления. Например, при затвердевании, охлаждении, осаждении, росте, отжиге материала в магнитном поле. В качестве примера на рис. 9.4 приведены кривые намагниченности пермаллоя (21.5%Fe-Ni), охлаждаемого c 600 ⁰С в присутствии (А, С) (т.н. «магнитный отжиг») и в отсутствие (В) магнитного поля [12]. Намагниченность измерялась вдоль (А) и поперек (С) направления поля во время охлаждения. Из рисунка видно, что при такой обработке возникает ОЛН, ориентированная вдоль внешнего поля. Аналогичным образом при росте нанокристаллических магнитных пленок создается одноосная магнитная анизотропия в направлении приложенного магнитного поля.

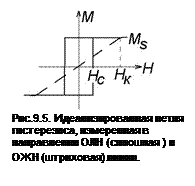Величина магнитной анизотропии определяется по величине внешнего поля, приложенного в жестком направлении, при котором достигается намагниченность насыщения в петле гистерезиса, рис.9.5.

Механизм появления наведенной магнитной анизотропии не всегда понятен. На рис. 9.6а приведена зависимость наведенной магнитной анизотропии в системе FeZrN от концентрации азота [13]. В системе FeXN, где Х = Ta, Zr, Tl и др. составляют лишь фракцию от 1 до нескольких ат. %, основным механизмом, согласно [13] является выстраивание, под влиянием магнитного поля при осаждении, атомов азота, занимающих тетраэдрические междоузельные позиции в решетке α-Fe, рис.9.6б. При этом смещение атомов Fe, окружающих внедренный атом N, оказывается неодинаковым, что и создает выделенное направление.

 

Микромагнитный риппл.

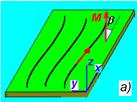
Из сказанного выше следует, что степень подавления магнитокристаллической анизотропии в нанокристаллических материалах зависит от соотношения размера зерна и обменной длины. Усреднение магнитокристаллической анизотропии обычно не бывает полным. Это приводит к отклонениям вектора намагниченности М относительно среднего направления < M >, совпадающего, в отсутствие внешнего поля, с ОЛН, рис. 9.7. Обменные силы при этом упорядочивают отклонения, сводя их к достаточно систематическим осцилляциям, описываемым небольшим набором гармонических членов, а в простейшем случае к одноволновому приближению.

Рис.9.7. Микромагнитный риппл (a), наблюдаемый в ЛПЭМ(в,д) и изображение в фокусе того же участка поверхности (б,г) [14].

Экспериментальные доказательства существования микромагнитных осцилляций получены из многочисленных наблюдений методом лорентцевской просвечивающей электронной микроскопии (ЛПЭМ). На рис. 9.7 приведены примеры изображений ПЭМ в фокусе микроскопа (б,г) и дефокусированные изображения (в,д - режим Френеля, один из методов ЛПЭМ) [14]. Принцип наблюдения микромагнитного риппла тот же, что и доменных границ, рис. 7.10. Электроны, проходя через магнитную пленку, испытывают воздействие силы Лоренца и отклоняются, создавая усиление и ослабление интенсивности в плоскости изображения, смещенной относительно фокальной плоскости микроскопа [15]. Следует обратить внимание на то, что осцилляторное отклонение намагниченности (рис.9.7а) передается в ЛПЭМ-изображении как прямолинейная вариация контраста (рис.9.7в).

 

Теория Хоффманна.

Хоффманном была развита теория [16,17], согласно которой, скоррелированные осцилляции намагниченности порождают магнитные полюса и соответствующее внутреннее поле рассеяния (ВПР, stray field). Конфигурация магнитного поля в ферромагнетике определяется балансом 5-ти вкладов в полную энергию:

1) обменной энергии

ε_ex = A (grad β)²; (9.9)

2) энергии одноосной анизотропии

ε_u = K_usin²β; (9.10)

3) энергии магнитокристаллической анизотропии

ε_k = Kf(φ,α₁,α₂,α₃); (9.11)

4) магнитостатической энергии

ε_m = -HMcos(β-θ); (9.12)

5) внутреннего поля рассеяния

ε_st = -(1/2) H _st M. (9.13)

Здесь А – плотность обменной энергии, β – угол локального отклонения намагниченности от среднего направления; θ – угол между внешним полем и намагниченностью, K_u – константа одноосной анизотропии, К – константа магнитокристаллической анизотропии, α₁,α₂,α₃ – направляющие косинусы магнитного момента в решетке кристаллита, H _st – внутреннее поле рассеяния. Стабильная конфигурация может быть получена вариационным методом:

dE =d∫∫∫_V(ε_ex+ε_u+ε_k+ε_k+ε_m+ε_st) =0 (9.14)

Интегрирование происходит по объему ферромагнитного связывания, который, в свою очередь, зависит от среднего размера зерна, магнитных параметров вещества и величины приложенного магнитного поля. В частности, величина остаточной магнитокристаллической анизотропии K_eff зависит от числа кристаллитов N в объеме обменного связывания:

K_eff = K/N^1/2, (9.15)

в соответствии с (9.1). Хоффманном теоретически показано, что область обменного связывания является эллипсоидом, вытянутым в направлении, перпендикулярном ОЛН, как схематично показано на рис. 9.8. Длина полуоси эллипсоида вдоль ОЛН

l_L ≈(A/K_u)^1/2(H_L/H_k+1)^-1/2, (9.16)

где H_k=2K_u/M_s. Т.е. при отсутствии внешнего поля (Н_L=0, индекс L символизирует направленность вдоль ОЛН) (9.16) совпадает с (9.2) для обменной длины δ₀. В поперечном направлении (вдоль оси жесткого намагничения) область обменного связывания составляет несколько микрон и более, т.е. может охватывать всю толщину ферромагнитной нанокристаллической пленки. Это согласуется с представлением о том, что поперечные осцилляции намагниченности подавлены обменным взаимодействием.

Точное решение вариационной проблемы (9.14) осложняется необходимостью учитывать вклад внутреннего поля рассеяния (9.13). Ниже приводится оценка этого вклада для наиболее простого вида осцилляций.

 

Внутреннее поле рассеяния (ВПР).

Пусть в пленке, расположенной в плоскости xy, среднее направление ОЛН будет параллельно оси х. Для простоты представим себе, что отклонение локальной ОЛН от среднего направления ОЛН подчиняется гармоническому закону. Т.е., локальная намагниченность имеет вид

Mx = M cosb, My = M sinb, где b = b­­₀ sin(2px/l). (9.17)

Для тонкой пленки z-компонента намагниченности полностью компенсируется размагничивающим полем. В (9.17) мы учитываем только продольные осцилляции вектора намагниченности, поскольку, как показано [16,17], поперечные осцилляции энергетически не выгодны. Кроме того, считаем, что вариации М однородны по толщине пленки. Соответственно, для наведенного магнитного заряда можно записать:

r(r) = - div (M) = Msinb(¶b/¶x) - Mcosb(¶b/¶y) = (pMb₀²/l) sin (4px/l),(9.18)

т.е. вариация наведенных магнитных зарядов происходит только в направлении оси x. Для магнитного потенциала имеем:

U = òòòr(r’)/| r’-r₀ |dV’, (9.19)

И для ВПР:

H _str(r₀) = - grad (U). (9.20)

Следуя (9.19) и (9.20) для у -компоненты ВПР в пленке, толщиной d и бесконечной в плоскости xy, получаем [18],

H_str,y = -¶U/¶y =

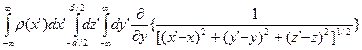=- =0, (9.21)

поскольку после дифференцирования мы будем иметь интеграл от нечетной функции в симметричных пределах.

Ввиду конечной толщины пленки, полной взаимной компенсации ВПР магнитных зарядов вдоль оси z не происходит. Для z -компоненты поля рассеяния имеем:

H_str,z = -¶U/¶z = -pM_ob_0²sin(4px/l)х 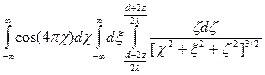, (9.22)

где z= (z’-z)/l, x=(y’-y)/l, c=(x’-x)/l. Интеграл в (9.22) берется точно, окончательно имеем:

H_str,z = -pM_ob_0²sin(4px/l)S_z, (9.23)

где S_z = (1/4)exp(-2pd/l)sh(4pz/l). (9.24)

При толщине d более 0.6 l z -компонента поля рассеяния становится пренебрежимо слабой.

Аналогично, для x -компоненты ВПР можно получить:

H_str,x = - pM_ob_0²cos(4px/l)S_x(z), (9.25)

где S_x(z) = =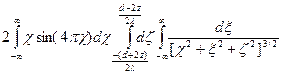

= exp[-p(d-2z)/l]sh[p(d-2z)/l]+ exp[-p(d+2z)/l]sh[p(d+2z)/l]. (9.26)

 

Амплитуда угловой дисперсии, полученная Хоффманном [16]

β₀ = DK/{(4πM)^1/2(2d)^1/4[AK_u(H_L/H_K+1)^3/8]}, (9.27)

где D- размер зерен, d – толщина пленки.

 

Теоретическая длина волны осцилляций [16].

λ=2π(A/K_u)^1/2(H_L/H_K+1)^-1/2 = 2πl_L. (9.28)

Таким образом, длина волны в 2π-раз больше обменной длины в продольном направлении.

 

 

X. ДИНАМИКА НАМАГНИЧЕНИЯ

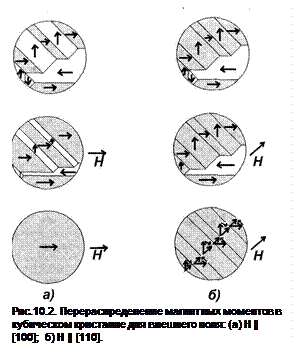
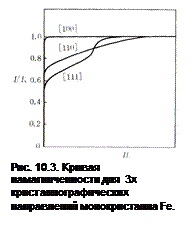
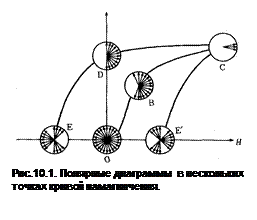С ростом величины магнитного поля, как мы знаем, происходит переориентация магнитных моментов в образце вдоль направления внешнего поля. На рис. 10.1. показаны полярные диаграммы в нескольких точках кривой намагничения. Намагниченность возрастает при движении от равномерного распределения магнитных моментов в размагниченном состоянии (О) до ориентированного вдоль поля в состоянии, близком к насыщению (С). Намагниченность падает при уменьшении поля от насыщения до остаточной намагниченности (D), далее до нуля при H=-H_c, где моменты компенсируют друг друга. В главе VI мы рассматривали лишь один механизм намагничения за счет движения доменных стенок таким образом, что домены с выгодной ориентацией намагничения растут за счет доменов с менее выгодной ориентации. Другим механизмом является намагничение за счет вращения магнитных моментов. На рис. 10.2 схематично изображено перераспределение магнитных моментов в кубическом кристалле для внешнего поля Н || [100] (т.е. вдоль ОЛН) (a) и H || [110] (б). В первом случае намагничение происходит за счет движения границ, во втором случае частично за счет смещения границ и частично за счет вращения магнитных моментов. Сложный вид кривой намагниченности на рис. 10.3 для направления [111] монокристалла Fe отражает композицию указанных механизмов намагничивания.

 

Намагничение смещением доменных стенок

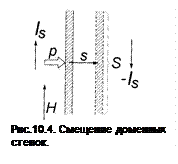
Смещение доменных стенок можно представить как обычное смещение под действием гипотетического давления р, при котором стенка площадью S смещается на некоторое расстояние s, рис. 10.4. Работа по перемагничиванию для поля параллельного 180⁰-стенки при этом равна механической работе давления

W = 2I_sSsH = pSs. (10.1)

Отсюда p = 2I_sH (10.2a)

Для поля, направленного под углом θ к I_s

p = 2I_sHcos θ. (10.2б)

Для 90⁰-стенки и поля, ориентированного под углами θ₁ и θ₂ к I_s по обе стороны от стенки

p = 2I_sH(cos θ₁-cos θ₂). (10.2в)

Доменные стенки не являются жесткими [1]. Если стенка связана дефектами, то под давлением поля она может упруго прогибаться [2], рис. 10.5. Если поле направлено под углом θ к намагниченности I_s, давление (10.2б) «выдавливает» стенку в виде фрагмента цилиндрической поверхности радиуса r так, что для стенки с плотностью энергии σ выполняется соотношение

σ/r = p = 2I_sHcosθ. (10.3)

Прирост намагниченности за счет изгиба стенки

ΔI = (4/3) I_s (cosθ)Ss, (10.4)

где S – площадь доменных стенок на единицу объема. Поскольку s приблизительно равно

s = l²/(8r), (10.5)

то ΔI = (Sl²I_s²/3σ)Н cos² θ. (10.6)

В тех случаях, когда <cos²θ> =1/3, получаем для 180⁰-стенок

χ_a,180 = S l² I_s² /(9σ) (10.7)

Для точек пиннинга (связывания) в виде немагнитных включений или пор, упорядоченных в кубическую сверхструктуру с периодом l имеем

χ_а = 2lI_s²/(9σ) (10.8)

Для железа I_s = 2.15 (Вб/м²), σ = 1.6 10^-3 Дж/м², и l = 10^{-4 м, получаем,}

<μ_a>≈ <χ_a>≈ 2x(2.15)² x10^-4/[9x1.6x10^-3x4πx10^-7] = 51 000

Хорошо отожженное чистое железо имеет <χ_a> ≈ 10 000. Т.е. столь грубая модель дает верный порядок величин.

Когда поле становится достаточно сильным, стенка отрывается от точек пиннинга, смещение становится необратимым. Вариация энергетического профиля обусловлена, как впервые заметил Кондорский [3], хаотично распределенными внутренними напряжениями. Схематично энергетический профиль можно представить в функции смещения, как изображено на рис. 10.6. Смещение под давлением (10.2б), обусловленным полем, происходит до тех пор, пока оно не уравновешивается реставрирующей силой, обусловленной градиентом (!) потенциала

∂ε_w/∂s = p = 2I_sHcos θ. (10.9)

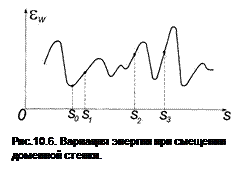Как только, смещение достигает точки s₁ на рис. 10.6, где градиент максимален, дальнейшее увеличение поля приводит к необратимому смещению стенки к другой точке равновесия s₂, где условие (10.9) удовлетворяется для нового значения поля. Если поле убирается, то стенка возвращается к ближайшему положению с минимумом потенциала. Таким образом, критическое поле, приводящее к устранению доменных границ обусловлено максимальным градиентом потенциального рельефа

H₀ = [1/(2I_scos θ)](∂ε_w/∂s)_мах. (10.10)

 

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: