Динамические свойства ферромагнетиков

 

Фактор магнитных потерь.

Желаемые характеристики высокочастотных, т.е. магнитомягких, ферромагнетиков – высокая восприимчивость и низкие потери при высоких частотах. Если материал помещен в переменное магнитное поле Н = Н₀ exp(iωt), то плотность магнитного потока В обычно запаздывает по фазе на угол δ вследствие энергетических потерь. Магнитная проницаемость тогда равна

μ = В/Н = В₀ exp(iωt-iδ)/ Н₀ exp(iωt) =(В₀/Н₀)exp(-iδ)=

= (В₀/Н₀)cosδ –i(В₀/Н₀)sinδ. (10.24)

Или μ = μ’– iμ’’, где μ’ = (В₀/Н₀)cosδ, μ’’= (В₀/Н₀)sinδ. (10.25)

Здесь μ’ характеризует компоненту B, имеющую ту же фазу, что и Н, т.е. μ’- нормальная проницаемость. Мнимая часть проницаемости μ’’ характеризует компоненту В, отстающую от Н на угол π/2. Наличие такой компоненты требует подпитки энергией для поддержания изменяющейся во времени намагниченности независимо от причин запаздывания. Отношение

μ’’/μ’= tan δ, (10.26)

т.е. величину tan δ, называют фактором потерь. Качество магнитомягкого материала часто характеризуют параметром μ/tan δ.

Природа и характер магнитных потерь зависят от частоты ω. В низкочастотной области наиболее существенными оказываются потери, связанные с гистерезисом. Потери на гистерезис становятся менее значимыми при высоких частотах, поскольку смещение доменных границ, являющееся основной причиной гистерезиса, в этой области в значительной мере задавлены, уступая вращению намагниченности.

 

Потери на вихревые токи (eddy current loss).

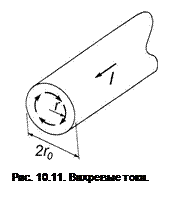Следующим по важности вклада в потери являются потери на вихревые токи. Изменение намагниченности вызывает вихревые токи, препятствующие такому изменению. В соответствии с законом электромагнитной индукции для контура с радиусом r с центром на оси цилиндра, рис.10.11,

∫E_sds = -∫∫(dB_n/dt) dS. (10.27)

Предполагая однородную намагниченность I, мы имеем

2πrE(r) = -πr²(dI/dt) и

E(r) = -(r/2)(dI/dt). (10.28)

Вихревой ток:

i(r) = -(r/2ρ) dI/dt, (10.29)

где ρ – удельное сопротивление. Потери на вихревые токи:

P = (1/πr₀²) ∫₀^r02πE(r)i(r)rdr = (1/2ρr₀²)(dI/dt)²∫₀^r0r³ dr =

= r₀²/(8ρ)(dI/dt)². (10.30)

Т.о. потери на вихревой ток пропорциональны квадрату скорости изменения намагниченности, т.е. квадрату частоты, если имеется полное проникновение в материал. Т.е. потери на вихревые токи будут возрастать с ростом частоты. Кроме этого, P ~ r₀². Это означает, что потери можно уменьшить путем разделения материала на электрически изолированные слои. Эффективным способом борьбы с вихревыми токами является увеличение сопротивления. Это реализуется в нанокристаллических пленках, получаемых испарением, электрохимическим осаждением и т.д. Тонкие пленки таких материалов используются, в частности, в быстродействующих и высокоплотных устройствах магнитной памяти. Высоким сопротивлением обладают прессованные из порошков сердечники трансформаторов, ферриты, особенно Ni-ферриты (~100 μΩ см), редкоземельные железные гранаты, не имеющие дивалентных металлов, типа Fe²⁺, снижающих сопротивление за счет прыжковой проводимости. Некоторые виды гранатов имеют настолько малые потери в области высоких частот, что становятся прозрачными для видимого света. Плата за это, как правило, низкая намагниченность насыщения и низкая восприимчивость.

Если dI/dt достаточно велико, то вихревые токи становятся достаточно большими, чтобы генерировать магнитные поля, сравнимые с внешним. Поскольку вихревой ток, который течет вокруг цилиндра радиусом r генерирует магнитное поле только внутри этого цилиндра, то интегрированное поле вихревого тока максимально в центре и уменьшается до нуля на поверхности цилиндра. Магнитное поле вихревого тока всегда препятствует изменениям намагниченности, вызывающим этот вихревой ток. Поэтому, намагниченность на оси цилиндра погашена. Амплитуда осцилляций намагниченности на поверхности уменьшается в е-раз на глубине

s = (2ρ/ωμ)^1/2, (10.31)

где ω – угловая частота изменяющегося магнитного поля и μ – проницаемость. Глубина s называется скин- слоем. Для магнитного металла с ρ = 1 10^‑7 Ω м (10μΩ см), <μ> = 500 и частоте 50 Гц скин слой составляет s = [2х1х10^-7/(2πх50х500х4πх10^-7)] ≈ 1.0х10^-3 (м) = 1 мм. При частоте 1 ГГц этот слой будет s≈2х10^-4мм=0.2μм. Исходя из этого, сердечники трансформаторов делают из тонких, электрически изолированных пластин, а для СВЧ не применяют толстых ферромагнитных пленок.

 

Магнитное последействие (magnetic after-effect).

Вихревые токи, вызывающие задержку фазы намагничивания в переменных магнитных полях, можно отнести к чисто электрическим явлениям. Изменение намагниченности также может происходить из-за изменений в фазовом составе или в структуре. Эти эффекты называются эффектами старения (aging). Под магнитным последействием понимают эффекты, связанные с магнитной вязкостью.

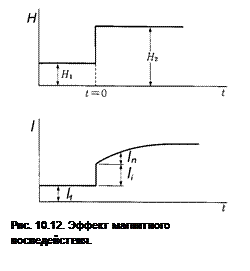
Эффект состоит в том, что при скачкообразном изменении приложенного к образцу магнитного поля с Н₁ до Н₂, намагниченность изменяется мгновенно с I₁ до I_i и затем плавно до насыщения, рис. 10.12. В простейшем случае зависящая от времени составляющая I_n(t) определяется одной константой релаксации τ, так что

I_n(t) = I_n0(1-exp(-t/τ)). (10.32)

Общий вид намагниченности имеет вид

I = χ_aH{1+ζ(1-exp(-t/τ))}, (10.33)

где ζ = I_n0/ I_i. Дифференциальное уравнение

d(I-χ_aH)/dt = -{ I-χ_aH(1+ ζ)}/τ (10.34)

описывает поведение намагниченности (10.33).

При осциллирующем магнитном поле

H = H₀exp(iωt), (10.35)

намагниченность испытывает задержку по фазе

I = I₀exp (iωt –iδ). (10.36)

Подставляя (10.35) и (10.36) в (10.34) получаем

tan δ = ζωτ/(1+ζ+ω²τ²), (10.37),

I₀=ωτχ_aH/(ωτcosδ–sin δ). (10.38)

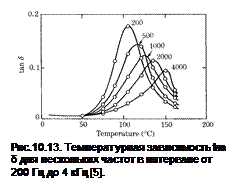
Так же как и в случае вихревых токов, в эффекте магнитного последействия δ называют углом потерь, а tan δ – фактором потерь. Фактор потерь зависит от частоты и температуры. Как видно из рис. 10.13, tan δ имеет максимум при определенной температуре. Температурная вариация обусловлена изменением времени релаксации с температурой. Рассматривая tan δ как функцию τ, получаем, что максимум приходится на

τ = (1+ζ)^1/2/ω. (10.39)

Наиболее простое объяснение этому эффекту дал Сноек [5]. Переменное магнитное поле, согласно модели Сноека, подобно шарику, осциллирующему под действием переменной силы взад и вперед по вогнутой поверхности, покрытой вязким слоем, рис.10.14. При низкой температуре, вязкий слой становится жестким, и шарик движется по твердой поверхности с малой потерей энергии, а при высокой температуре шарик движется по слою с низкой вязкостью, также не требующей больших затрат. При промежуточных температурах затухание колебаний шарика будет максимальным.

Ферромагнитный резонанс.

Ферромагнитные материалы интенсивно поглощают электромагнитное излучение некоторой резонансной частоты, определяемой самим материалом, его формой и внешними условиями, например, присутствием постоянного магнитного поля. Ферромагнитный резонанс (ФМР) – один из видов магнитного резонанса в твердом теле, но в отличие от электронного парамагнитного резонанса (ЭПР) и ядерного магнитного резонанса (ЯМР), он определяется взаимодействием переменного поля с макроскопической коллективной намагниченностью образца. Это приводит к гораздо более сильному поглощению в резонансе. Явление ФМР было предсказано в 1913 г. В.К. Аркадьевым [6] из классических, а в 1923 г. Я.Г. Дорфманом из квантовых соображений [7]. В 1935 г. Л.Д. Ландау и Е.М. Лифшиц вывели уравнение движения магнитного момента, являющегося основой классической теории ФМР [8]. В 1948 г. Ч. Киттель получил важные соотношения, учитывающие влияние формы образца и магнитной анизотропии [9]. Экспериментально ФМР был обнаружен Грифитсом [10] и Завойским [11].

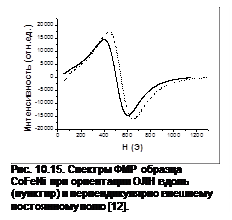Установки (спектрометры) ФМР бывают двух типов. Первый - принципиально не отличается от установок ЭПР и включают в себя генератор СВЧ, волновод и резонатор с исследуемым образцом, детектор с системой индикации амплитуды СВЧ и систему обеспечения постоянного поля, сканируемого в определенном интервале значений, рис.10.15. Во втором, сканирование производится изменением частоты СВЧ при установленном магнитном поле (или в его отсутствие).

Если внутреннее магнитное поле Н и намагниченность М в материале однородны, то они связаны с внешим полем Н_е соотношением

H = H_e – Ň M, (10.40)

где Ň – симметричный тензор размагничивания. Рассмотрение Киттеля ФМР в ферромагнитном эллипсоиде показывает, что этот тензор в осях координат, совпадающих с осями эллипсоида, становится диагональным и его компоненты называются размагничивающими факторами. Их сумма

N_x + N_y + N_z = 4 π. (10.41)

В режиме фиксированной частоты СВЧ – излучения ω₀, резонанс будет происходить при значении постоянного поля H_r, определяемом соотношением

ω₀ = g{[H_r + (N_y-N_z)M][H_r+(N_x-N_z)M]}^1/2, (10.42)

где, также как и в (9.8), гиромагнитный фактор g = gm_B = geħ/(2m) = 1.105·10⁵g (м/(Ас)), g= 2.023≈2 – фактор спектроскопического расщепления. Для сферы N_x = N_y = N_z = 4 π /3, поэтому

ω₀ = gH_r. (10.43)

Для плоской пластины, если внешнее поле направлено перпендикулярно поверхности, то N_x = N_y = 0 и N_z = 4 π и

ω₀ = g(H_r – 4πM). (10.44)

Если же поле направлено вдоль пластины в плоскости xz, то N_x = N_z = 0 и N_y = 4 π и

ω₀ = g[H_r (H_r+4πM)]^1/2. (10.45)

Соотношения (10.42)-(10.45) называются соотношениями Киттеля [9]. Они приведены в системе единиц СГСМ. В системе СИ 4πM необходимо заменить на μ₀M.

В приведенных соотношениях пренебрегалось пока наличием магнитной анизотропии. Важным частным случаем является случай одноосной (наведенной) анизотропии. Показано, что в этом случае резонансное значение поля зависит от того, направлено ли поле вдоль «легкой» оси (ЕА), либо вдоль «жесткой» оси (HA). Соотношения Киттеля в этом случае имеют вид, соответственно:

ω² = g²(H_r^EA + H _k )(H_r^EA + H _k + 4πM) (10.46)

ω² = g²(H_r^HA - H _k )(H_r^HA - H _k + 4πM), (10.47)

где H _k – поле одноосной анизотропии.

 

Уравнение Ландау-Лифшица.

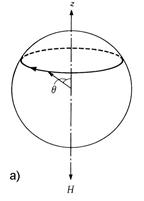
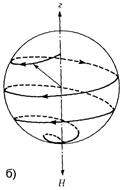
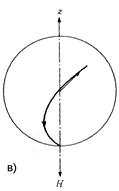
Рис. 10.16. Прецессия магнитного момента в поле Н без затухания (а), со слабым затуханием (б) и с сильным затуханием (в)

При включении магнитного поля магнитный момент начинает прецессировать, рис.10.16а. Благодаря коллективному характеру, магнитный момент M (намагниченность) некоторого объема (макроскопического,микроскопического, наноразмерного) магнитного вещества имеет несопоставимо большее значение, чем магнитный момент изолированного иона и, следовательно, расщепление прецессия может рассматриваться как классическое движение, а не как квантовый перескок между соседними достаточно разнесенными уровнями. Ландау и Лифшиц впервые предложили описание прецессии магнитного момента с учетом затухания [8], в виде уравнения, называемого уравнением Ландау-Лифшица (Л-Л):

d M /dt = -g(M ´Н_eff )+ R. (10.48)

Эффективное магнитное поле Н_eff включает постоянное H₀ и СВЧ H_rf поля Н_eff = H₀ + H_rf. R – диссипативный член в форме Л-Л

R = -(λ/M²) (M´ ( M´H_eff )), (10.49)

в форме, познее предложенной Гильбертом [13]:

R = (α/M) (M´ (dM / dt), (10.50)

в форме Блоха-Бломбергена [14]

R =-ω_r (M – (M₀/H₀) H_eff), (10.51)

где M₀ – постоянная составляющая магнитного момента, ω_r –резонансная частота. В используемом линейном приближении и при малых потерях эти три формы эквивалентны и входящие в них параметры связаны соотношением

λ = αgM₀ = ω_rM₀/H₀. (10.52)

Уравнение Ландау-Лифшица с диссипативным членом в форме Гильберта

d M /dt = g(M ´Н_eff )- (ag/M)(M ´ (M ´Н_eff )), (10.53)

часто используется для исследования динамики микромагнитных процессов. Если затухания нет, т.е. α = 0, то магнитный момент будет двигаться по боковой поверхности конуса неограниченно долго, рис. 10.16а. При сильном же затухании магнитный момент развернется вдоль поля, не сделав ни одного оборота, рис. 10.16в.

 

 

Размерный резонанс.

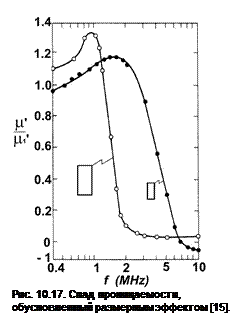В практических приложениях внешнее постоянное магнитное поле и, соответственно, постоянная составвляющая намагниченности могут отсутствовать, что не исключает проявлений магнитного резонанса. Было замечено, что при достаточно больших размерах сечений сердечников магнитов на частотах (в МГц-диапазоне) выше определенной появляется спад в проницаемости [15]. Спад смещается в сторону больших частот, если сечение уменьшается, рис. 10.17. Этот спад был отнесен за счет стоячих электромагнитных волн, распространяющихся в сердечнике. Скорость распространения электромагнитной волны в среде уменьшается в сравнению со скоростью в вакууме. Соответственно, длина волны будет

λ = с/[f(<ε><μ>)^-1/2]. (10.54)

Здесь f – частота, <ε> и <μ> относительные диэлектрическая и магнитная проницаемости. При <ε> ~ 5 10⁴ и <μ> ~ 10³, характерных для Mn-Zn- ферритов, где этот эффект был обнаружен [15], для f=1.5 МГц длина волны λ должна быть равной 2.6 см, что близко по значению с размерами сердечника. Если размеры кратны длине волны, то электромагнитные волны будут резонировать в сердечнике, создавая стоячую волну. Спад в зависимости μ’(f) обусловлен резонансным поведением, получившим название размерного резонанса.

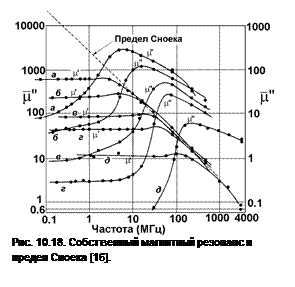
Собственный магнитный резонанс.

В области высоких частот проницаемость падает, а магнитные потери растут благодаря магнитному резонансу. На рис. 10.18 представлены зависимости действительной и мнимой частей проницаемости для ферритов Ni-Zn с разным химическим составом [16]. Можно заметить, что материалы с более высокой проницаемостью имеют более узкий частотный диапазон. Сноек [17] объяснил этот эффект как следствие резонанса вращения намагниченности под действием поля анизотропии. В соответствии с уравнением (10.46), резонансная частота может быть получена при Н =0 и М =0, что дает

ω = γН_k. (10.55)

Если включается высокочастотное поле с частотой (10.55), то вращение намагниченности вокруг ОЛН будет резонировать с полем, что приведет к резкому изменению μ’ и μ’’. Если взять К₁ = -5 10² Дж/м³, М_s = 0.3 Тл, для ферритов Ni-Zr, мы можем оценить поле анизотропии по (10.23б)

Н_К = (4х5х10²)/(3х3х10^-1) ≈ 2.2х10³(А/м) (≈27 Э).

Полагая g =2, из (10.54) имеем

ω = (1.105х10⁵)х2х2.2х10³) ≈ 5х10⁸, f = ω/(2π) ≈ 8 10⁷Гц (80 МГц). Это значение находится в области, где наблюдается резонанс. Явление называется собственным магнитным резонансом, рис.10.18.

 

Предел Сноека.

Для материала с положительной анизотропией К₁>0, согласно (10.23а),

Н_К = 2К₁/I_s.

Резонансная частота ω = 2gК₁/ I_s. (10.56)

С другой стороны, увеличение К₁ ведет к уменьшению проницаемости:

<μ>=I_s²/(3K₁μ₀). (10.57)

Перемножая это, получаем

ω<μ> = 2gI_s/(3μ₀). (10.58)

Аналогичное соотношение справедливо и для К₁<0. Полагая I_s = 0.3 Тл и μ= 4π х 10^-7<μ>, имеем

f<μ> ≈ 5.6 х 10⁹ = 5.6 ГГц. (10.59)

Линия на рис. 10.18 проведена через точки, где μ’ составляет 0.5 от своего максимального значения. Условие (10.59) примерно совпадает с этой линией. Линия называется пределом Сноека. Он ограничивает величину проницаемости условием (10.59) для материалов с кубической анизотропией. В материалах с особым типом анизотропии, предел Сноека может нарушаться.

Устойчивая доменная структура в переменных полях.

Стационарная картина доменов деформируется или полностью меняется, если образец подвергается воздействию переменного магнитного поля. При этом возможны устойчивые конфигурации доменов, форма которых весьма чувствительна как к небольшим изменениям параметров внешнего поля, так и к микроструктуре и электрофизическим параметрам материала. На рис. 10.19 представлены динамические доменные картины наблюдаемой на одном и том же месте пленки феррита-граната толщиной 9 мкм в переменном магнитном поле с частотой, увеличивающейся последовательно - от (а) к (г) - от 10 кГц до 100 кГц и варьируемой амплитудой H₀.

	а	б	в	г
	Рис. 10.19. Эволюция динамических доменных структур. Частота поля увеличивается от (а) к (г) [18].

При некоторых комбинациях f и H_о весь образец может оставаться намагниченным в одном направлении. Кристалл как бы перестает "замечать" переменное поле, никак не реагирует на него. Реализуется так называемая динамическая однодоменность.

 

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: