Кинетостатический (силовой) расчет механизма

Теория механизмов и машин

 

Пояснительная записка к курсовому проекту

 

 

Студент: ______________________________

______________________________

Группа: ЭСЭУ-3 (СП)

 

 

Севастополь 2012

СИНТЕЗ И КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ

РЫЧАЖНОГО МЕХАНИЗМА

 

№ вар.	noa об/мин	Размеры звеньев, мм
OA	AB	BD	CB	DE
10.0

 

Таблица 1. Таблица кинематических пар:

Обозначение пары	Подвижность пары	Звенья, образующие пару	Вращ., пост.
0-1	одноподвижная	Стойка-кривошип	вращательная
1-2	одноподвижная	Кривошип-шатун	вращательная
2-3	одноподвижная	Шатун-коромысло	вращательная
3-0	Одноподвижная	Коромысло-стойка	вращательная
3-4	одноподвижная	Коромысло-шатун	вращательная
4-5	одноподвижная	Шатун-ползун	вращательная
5-0	одноподвижная	Ползун-стойка	поступательная

 

Количество звеньев механизма: 5

Количество низших кинематических пар : 7

Определяем степень свободы механизма:

(1.1)

Механизм работает, одно ведущее звено.

1.1 Описание построений плана положений механизма.

Примем длину кривошипа 0,05 м. Рассчитаем масштабный коэффициент по формуле:

м/мм (1.2)

В этом масштабе вычерчиваем планы механизма в 12 равноотстоящих положениях кривошипа. За нулевое принимаем одно из крайних положений механизма. Для этого необходимо найти длины от­резков всех остальных звеньев механизма, которые будут изображать их на чертеже:

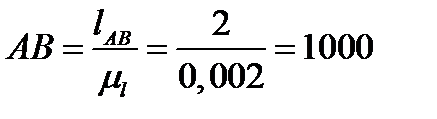мм, (1,3)

мм, (1.4)

и так далее.

1.2 Описание построения диаграмм перемещения, скоростей, ускорений ползуна E.

Диаграмму перемещения строим в координатах S, На оси абсцисс откладываем отрезок L=120 мм, изображающий полный угол поворота кривошипа. Делим этот отрезок на 12 частей. Таким образом, получаем масштабный коэффициент оси φ.

(1.5)

По оси ординат откладываем перемещения ползуна S, полученные из плана положений. Для этого измеряем величину отрезков от нулевого положения ползуна до текущего. Откладываем их на диаграмме перемещений от соответствующих точек оси абсцисс вертикально вверх в масштабе:

Полученные точки соединяем плавной кривой.

Диаграмма скорости ползуна строится методом графического дифференцирования диаграммы перемещений. Для этого под диаграммой перемещений строим оси координат и φ. На продолжении оси абсцисс - слева откладываем отрезок длиной .

Из точки проводим лучи, параллельные координатам кривой S(φ) на соответствующих участках. Эти лучи продолжаем до пересечения с осью ординат . Затем от точек пересечения проводим прямые, параллельные оси абсцисс до середины соответствующего участка. Полученные точки соединяем плавной кривой.

Имея диаграмму скорости ползуна, аналогично построим диаграмму тангенциальных ускорений ползуна. Масштабный коэффициент для диаграмм остаётся неизменным. На продолжении оси абсцисс φ влево откладываем отрезок .

Угловая скорость вращения кривошипа определяется по формуле:

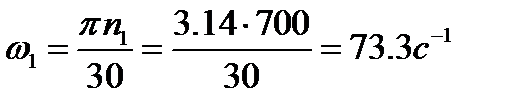(1.6)

Масштабные коэффициенты осей и найдём по формулам:

(1.7)

(1.8)

1.3. Описание построения планов скоростей

Рис.1

Рассмотрим построение плана скоростей для 5 положения. Выбираем произвольно полюс Р (рис.1) и откладываем от него отрезок перпендикулярно к звену ОА в сторону вращения кривошипа вектор, Pa=40 мм, изображающий скорость в масштабе:

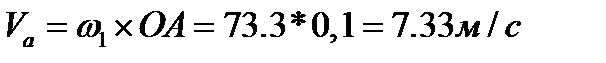(1.9)

(1.10)

Скорость точки В находится из условия:

(1.11)

(1.12)

Векторы относительных скоростей V_ВA и V_BC известны только по направлению. Вектор относительной ско­рости V_ВA перпендикулярен звену AВ, а вектор V_ВC — звену CВ.

Точка C неподвижна, поэтому V_C=0. Таким образом, рассматри­ваемая группа присоединена к двум точкам, скорости которых известны и по направлению, и по величине.

В соответствии с векторным уравнением (1.11) на плане скоростей прово­дим через точку (а) прямую, перпендикулярную звену AВ. Это есть ли­ния вектора V_BA. В соответствии с векторным равенством (1.12) про­водим через точку C на плане скоростей прямую, перпендикулярную звену CB. Это будет линия вектора V_CB. Точка (в) пересечения этих двух пря­мых и будет определять конец вектора, изображающего на плане скоро­стей вектор Vв. Чтобы определить истинную величину любого из векто­ров в м/с, надо его длину умножить на масштаб плана скоростей.

Напри­мер:

Для определения скорости точки D воспользуемся тем, что кар­тина относительных скоростей образует на плане скоростей фигуру, по­добную фигуре звена и повернутую относительно ее на 90° в сторону вращения звена. В соответствии с этим отрезок рb плана скоростей раз­делим в отно­ше­нии DВ: CB, т. е.

Откуда

Величина скорости точки D, м/с

Для определения скорости точки E напишем векторные уравнения

 

(1.13)

(1.14)

Вектор относительной скорости V_ED и вектор абсолютной скорости V_E не известны по величине, но известны по направлению. В соответствии с векторным уравнением через точку D на плане скоростей проводим пря­мую, перпендикулярную звену ED. Это будет линия относительной скоро­сти, где далее проводим линию параллельно направляющей

Х-Х. Точка E, пе­ресечения этих прямых и есть искомая точка. Истинная величина скорости точки E, м/с

Определим угловые скорости. Угловая скорость звена 2, рад/с, оп­ределяется по формуле

(1.15)

Чтобы определить направление угловой скорости w₂, следует век­тор относительной скорости V_BA перенести в точку В механизма, а точку A мысленно закрепить. Тогда вектор V_BA будет стремиться вращать звено 2 по ходу часовой стрелки. Это и будет направление угловой ско­рости w₂

Остальные угловые скорости:

(1.16)

(1.17)

Угловая скорость w₃ направлена против часовой стрелки, w₄ — по часовой стрелке.

Таблица 2. Таблица линейных и угловых скоростей звеньев в 12 положениях.

 

1.4. Описание построения планов ускорений

Рис.2

Рассмотрим построение плана ускорений на примере некоторого положения. Из произвольного полюса (рис.2) откладываем вектор, параллельный звену ОА и направленный от точки А к точке О. В нашем случае величина =50 мм, изображающий ускорение в масштабе:

(1.18)

(1.19)

Для определения ускорения точки В напишем уравнение, рассмотрев движение точки В относительно точек A и C:

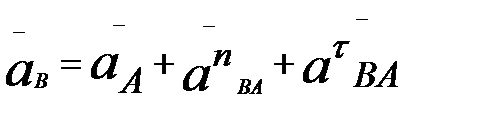(1.20)

(1.21)

Ввиду того, что у точки А будет только нормальное ускорение и не будет тангенционального.

Нормальные ускорения можно определить по величине и направ­ле­нию. Величина вектора

(1.22)

(1.23)

Вектор 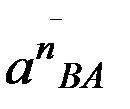направлен вдоль звена AВ от точки В к точке A (к цен­тру относительного вращения). Вектор 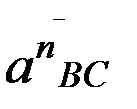направлен вдоль звена BC от точки B к точке С.

Для того, чтобы построить ускорение точки В на плане ускорений, нужно из конца вектора отложить вектора в следующей последовательности:

,

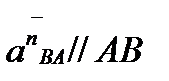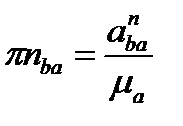
Затем строим сумму векторов правой части векторного уравне­ния (1.21). Для этого проводим из полюса параллельно звену СВ вектор a ⁿ_BС. Его масштабная величина на плане ускорений pn_bc = a ⁿ_ВC/m_a. Затем через точку n_bc перпендикулярно звену CВ проводим вектор тангенци­аль­ного ускорения a ^t_BC. Пересечение векторов a ^t_BC и a ^t_BA определит точку b. Вектор n_bab выражает ускорение a ^t_BA, а вектор n_bcb выражает уско­рение a ^t_BC.Если соединить точку а с точкой b на плане ускорений, то вектор аb выра­зит полное относительное ускорение a _BA, так как является геометрической суммой векторов a ⁿ_BA и a ^t_BA. И, наконец, вектор pb выражает на плане ускорений вектор абсолютного ускорения точки В.

Для определения ускорения точки D воспользуемся свойством по­добия. На основании теоремы подобия имеем

Тогда

Для определения ускорения точки E напишем векторное уравне­ние

(1.24)

Рассмотрим векторы, входящие в данное уравнение. Вектор a_D мы определили ранее. Величина вектора aⁿ_ED, м/с², определяется по формуле

(1.25)

а остальные векторы известны только по направлению.

Достраиваем план ускорений. Из точки d параллельно звену ED проводим вектор a ⁿ_ED, масштабная величина которого, мм, на плане ус­ко­рений равна dn_ed = a ⁿ_ED /m_a

Через точку перпендикулярно звену DE проводим вектор a ^t_ED, а через точку p параллельно направляющей — вектор a _E. На пересечении векторов a ^t_ED и a _E получим точку e, которая определит их ве­личины. По­лученный вектор n_ede на плане ускорений выражает в масштабе ускорение a ^t_ED, а вектор pe является изображением вектора ускорения a _e. Если соединить точку (d) с точкой (e), то вектор de будет изображать пол­ное от­носительное ускорение a _ED.

1.5 Определим угловые ускорения. Ведущее звено 1 вращается с по­стоянной угловой скоростью, поэтому его угловое ускорение e₁=0.

Угловое ускорение звена 2, с^-2, равно величине тангенциального (касательного) ускорения a ^t_BA, деленной на длину звена AB, т.е.:

 

(1.26)

 

Чтобы определить направление углового ускорения e₂, вектор от­но­сительного ускорения a ^t_BA следует перенести с плана ускорений в точку В механизма, а точку A мысленно закрепить. Тогда вектор a ^t_BA бу­дет стре­миться вращать звено 2 против хода часовой стрелки. Это и бу­дет направ­ление e₂.

Подобным образом находим угловые ускорения остальных звеньев;

 

(1.27)

(1.28)

e₃ направлен против хода часовой стрелки, e₄ направлен по ходу часовой стрелки.

Таблица3. Таблица ускорений для 0-го и 5-го положений.

 

	686,51	386,27
	257,44	257,44
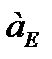
	457,64	202,44
	394,62	95,5
	686,51	384,5
	168,1	155,36
	986,55	238,75
	3813,94	2136,11
	373,56	345,24

 

КИНЕТОСТАТИЧЕСКИЙ (СИЛОВОЙ) РАСЧЕТ МЕХАНИЗМА

 

№ вар.		Веса звеньев, Н
OA	AB	BD	Е	DE
10.0

 

К механизму машины во время ее движения приложены различные силы. Это движущие силы, силы сопротивления, силы тяжести и другие. Ха­рактер действия сил может быть разным: некоторые из них зависят от поло­жения звеньев механизма, другие - от их скорости, силы могут быть и посто­янными. Своим действием приложенные силы сообщают механизму тот или иной закон движения.

Кинематические характеристики: скорость, ускорение, время сра­батывания и др. - определяются посредством решения уравнения движе­ния. Выбор способа решения уравнения движения зависит от характера дейст­вия заданных сил и от передаточных свойств механизма. При этом размеры, массы и моменты инерции звеньев должны быть известны. При этом необ­ходимо подчеркнуть, что при решении обеих задач предполагается, что все звенья механизма являются абсолютно жесткими.

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: