Описание построения диаграмм скорости, ускорения и перемещения толкателя.

Для построения диаграммы ускорений, по оси x отложим отрезок длинной 180 мм, представляющий собой угол поворота кулачка, равный 2 (или 360º), то масштаб углов поворота равен:

Далее переводим заданные углы , и в полученный мас­штаб и откладываем их на оси х.

Площади F₁ и F₂, а также F₂' и F₁ ' (рисунок 5.6) должны быть равны между собой, поскольку скорость толкателя в начале и конце углов удаления и возвращения равна нулю. Для того, чтобы получить равен­ство этих площадей на диаграмме, необходимо, чтобы наибольшие орди­наты h ' и h " обоих участков диаграммы (на углах удаления и возврата) берутся в отношении, обратно пропорциональном квадратам углов и , т.е.:

(3.4)

мм

Величину отрезка h' берется произвольно h'=50 мм, а затем по зависимо­сти (5.2) рассчитываем величину h"=50 мм. Далее строим диаграмму S" - так, чтобы она была симметричной относительно оси х.

Проинтегрируем дважды графически полученную зависимость. Для этого:

1)разбиваем угол удаления на 8 равных частей 01; 12; 23;...;

2)построим ординаты аb, сd,..., соответствующие серединам интервалов 01,12,.., и отложим отрезки Оb' = аb, Od’ =cd на оси ординат;

3) соединим произвольно взятую точку P₁ на продолжении оси х влево (получив полюсное расстояние O P₁ = 28,57 мм) с точками b ', d',...;

4) на графике у' (х) из точки O проводим отрезок Ob" в интервале O1 параллельно лучу P₁ b', отрезок b"d" в интервале 1-2 параллельно лучу P₁d' и т. д.

Далее разбиваем угол возврата на равные 8 частей и при том же полюсном расстоянии 28,57 мм повторяем пункты 2-4.

Полученная ломаная линия (в пределе - кривая) в графической форме представляет собой первый интеграл заданной зависимости, т. е. кри­вую и, значит, с учетом масштаба .

Аналогично, интегрируя кривую у' = у' (х), получаем вторую интегральную кривую у=у(x),с учетом масштаба S = S () (график у (х)).

В задании на проект задан максимальный ход толкателя . На кривой S - он представлен максимальной ординатой величина кото­рой определяется непосредственно на этой кривой после графического интегрирования. Зная и , можно найти масштаб , а именно:

Динамический синтез кулачковых механизмов

Задачей динамического синтеза в данном случае является определение такого минимального радиус-вектора профиля кулачка , при котором перемен­ный угол передачи движения ни в одном положении кулачкового механизма не будет меньше . Для этого необходимо построить диаграмму 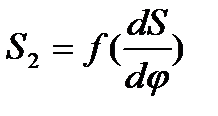, представляющую собой изменение перемещения толкателя () в зависимости от его скоро­сти (), графически исключив ось из диаграмм и .

На построенных координатах начинаем построение, для этого нам необходимо использовать две диаграммы - скорости и перемещения.

С диаграммы перемещения, замеряем отрезок по оси ординат, для текущего положения, и откладываем его на графике вдоль оси S из точки О. Затем по диаграмме скорости определяем скорость для данного положения и откладываем его параллельно оси абсцисс из полученной точки. Проделываем это действие для всех положений ползуна, полученные отрезки соединяем.

Далее проводим касательные прямые под углом (с обеих сторон полученного кулачка). Прямые в точке максимального подъёма толкателя пересекутся в некоторой точке, определяющей минимальный радиус кулачковой шайбы. Центр вращения кулачка выбираем в точке С, расположенной в области допустимых положений центров (заштрихована), образуемой прямыми. Это производится для избежания больших по величине локальных напряжений в зоне контакта кулачка с роликом.

ОС= – радиус начальной шайбы.

В нашем случае начальный радиус принят – =60 мм.