Определение реакций в группах Ассура

Делим механизм на группы Ассура и вычерчиваем каждую группу отдельно, отбросив связи и заменив их реакциями.

Решать начинаем группу, наиболее удаленную от кривошипа(рис.2.2 а).

а) б)

рис. 2.2

Составляем уравнение суммы моментов сил, действующих на сис­тему, относительно точки D. Таким образом избавляемся от двух неизвест­ных, которые дает реакция R₃₄, так как ее момент будет равен нулю:

Из этого уравнения определяем неизвестную реакцию R ₀₅:

 

Знак "-", полученный при расчете, показывает, что направле­ние реакции было выбрано неверно и его надо изменить на противоположное.

Далее составляем векторное уравнение суммы сил, действую­щих на звенья 4 и 5:

Векторное уравнение решается графически, методом построения плана сил в масштабе (см. рисунок 2.2 б ). Масштаб сил определя­ется через самую большую силу, приложенную к системе:

.

Переводим все известные силы в масштаб и строим много­угольник сил для группы 4-5.

1. Откладываем вектор в масштабе .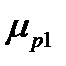

2. Из конца вектора произвольно откладываем вектора:

.

3. Соединяем начало вектора с концом получившегося вектора.

4. Это и будет сила реакции .

Опреде­ляем действительную величину реакции:

Рассматриваем группу звеньев 2 и 3.

 

 

а) б)

рис 2.3

Для упрощения расчетов вы­черчиваем звенья группы, разделив шарнир B (см. рисунок 2.3, а).

Рассматриваем звено AB. Составляем уравнение моментов сил, приложенных к звену, относительно точки B, так как сила R₁₂ не известна ни по величине, ни по направлению, разобьем ее на две составляющие и .

Знак "-", полученный при расчете, показывает, что направле­ние реакции было выбрано не правильно и его надо изменить на противоположное. Рассматриваем звено 2. Составляем уравнение моментов сил, приложенных к звену, относительно точки А (тем самым исключив из него момент неизвестной реакции R₁₂ ).

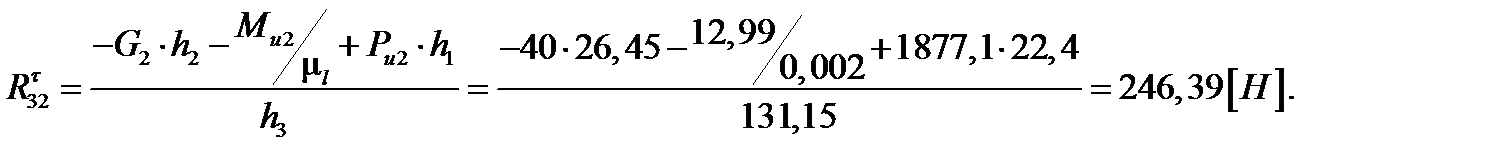
Знак "+", полученный при расчете, показывает, что направле­ние реакции было выбрано правильно.

 

Рассматриваем звено 3. Составляем уравнение моментов сил, приложенных к звену, относительно точки С (тем самым, исключив из него момент неизвестной реакции R_С3 ).

Знак "+", полученный при расчете, показывает, что направле­ние реакции было выбрано правильно.

Таким образом, мы определили обе составляющие реакции .

Далее составляем векторное уравнение суммы сил, действующих на звено 2, в которое войдут все внешние силы, обе составляющие реакции в точке B и реакция R₁₂ ..

Решая уравнение построением силового многоугольника (плана сил) в масштабе (рисунок 2.3, б), определим из построения величину и направ­ление реакции R₁₂. Определяем действительную величину реакции:

Составляем векторное уравнение суммы сил, действующих на звено 3, в которое войдут все внешние силы, обе составляющие реакции в точке B и реакция R_C3.

Решая уравнение построением силового многоугольника (плана сил) в масштабе , определим из построения величину и направление реакции R_C3(рисунок 2.3, б). Определяем действительную величину реакции:

Рассматриваем ведущее звено. Так как к ведущему звену приложен закон движения, степень подвижности этого звена W = 1, то есть оно не является статически определимой системен Для того, чтобы ведущее звено находи­лось в равновесии под действием приложенных к нему сил, необходимо учесть влияние привода (двигателя и редуктора), который и задает ведущему звену закон движения Для этого к ведущему звену прикладывают урав­новешивающую силу ли уравновешивающий момент. Уравновешиваю­щую силу прикладывают в крайнюю точку кривошипа (точку A на рис 2.4 а) перпендикулярно звену, так как в этом случае плечо этой силы относительно центра вращения звена (точки О) является максимальным. Таким образом, нам известна точка приложения уравновешивающей силы (центр шарнира А) и ее линия действия, а неизвестной является ее величина.

 

 

а) б)

рис 2.4

Составляем уравнение моментов сил, приложенных к звену, относительно точки О (тем самым исключив из него момент неизвестной реакции R₀₁ ).

Знак "+", полученный при расчете, показывает, что направле­ние реакции было выбрано правильно.

Составляем векторное уравнение суммы сил, действующих на звено 1:

Решая уравнение построением силового многоугольника (плана сил) в масштабе определим из построения величину и направление реакции R₀₁(рисунок 2.4, б). Определяем действительную величину реакции:

.

Силовой рычаг Жуковского.

План скоростей разворачиваем на 90˚.В соответствующие точки прикладываем силы, действующие на механизм. Моменты заменяем на пары сил. Производим расчёт суммы моментов относительно полюса.

 

 

Погрешность:

Силовой расчет заканчиваем определением мощности, которую не­обходимо приложить к ведущему звену, чтобы механизм совершал работу, для выполнения которой он создан. Для этого необходимо величину уравновеши­вающей силы умножить на скорость точки, в которую эта сила приложена:

 

3. Синтез кулачкового механизма

 

 

№ вар	n Об/мин				h мм
градусы

 

Плоские трехзвенные кулачковые механизмы состоят из стойки и двух подвижных звеньев, причем подвижные звенья образуют со стойкой низшие кинематические пары (вращательные или поступательные), а друг с другом -высшую кинематическую пару.

Ведущее звено в кулачковом механизме, имеющее переменный радиус кри­визны, называют кулачком, ведомое - толкателем.

В кулачковых механизмах за один оборот кулачка чаще всего наблюдается 4 фазы движения:

1-я фаза соответствует прямому ходу или удалению толкателя от центра вращения кулачка и описывается углом удаления ;

2-я фаза соответствует выстою толкателя в самой дальней точке профиля и описывается углом дальнего стояния (дальнего выстоя) ;

3-я фаза соответствует обратному ходу или возврату толкателя к центру вращения кулачка и описывается углом возврата ;

4-я фаза соответствует выстою толкателя в ближней точке профиля и описывается углом ближнего выстоя .

Очевидно, что:

+ + + =2 (3.1)

Сумму углов , 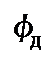и называют рабочим углом и обозначают :

+ + = . (3.2)

Определяем степень свободы механизма по формуле Чебышева:

, (3.3)

где

n — число подвижных звеньев;

p5—число кинематических пар 5-го класса (низшие кинематиче­ские пары).

р4—число кинематических пар 4-го класса (высшие кинематиче­ские пары).

О - низшая кинематическая пара (кп) 5-го класса, совершает вращательное движение;

А – высшая кп образованная звеном 1 и 2, 4-го класса;

В – низшая кп образованная звеном 2 и 3, 5-го класса, совершает вращательное движение;

С – низшая кп 5-го класса, совершает поступательное движение;

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: