Точность процесса обработки информации. Расчетное определение погрешностей.

В процессе обработки информации в ИС возникают погрешности вычислений, которые зависят от параметров алгоритма вычислений и технических характеристик устройств.

Погрешности делятся на погрешности аппроксимации, вычислительные погрешности, трансформационные погрешности, параметрические погрешности, динамические погрешности [4].

Погрешности имеют случайный характер и оцениваются законами распределения. В основном, для описания погрешностей пользуются симметричными законами распределений. Чаще всего они аппроксимируются нормальным и равномерным законами распределения. Параметрами этих законов распределения являются математическое ожидание и дисперсия.

Мерами погрешности вычислений могут быть:

– абсолютная погрешность единичного вычисления, оценивается в физических величинах значений y:

Δy = Аy – ay,

где Аy – истинное значение, аy – расчетное значение параметра;

- относительная погрешность вычисления, которая является безразмерной величиной:

,

или относительная приведенная погрешность вычислений:

,

где a_y^н - номинальное значение вычисляемого параметра или диапазон изменения параметра.

В зависимости от значения относительной приведенной погрешности вычислений различают вычислители (системы):

- прецизионные: δу<0,5 – 1,5%;

- точные: δу может принимать значения: 0,5%; 1,0%; 2,5%;

- невысокой точности: δу до 10%.

В технических системах управления используются точные вычислители.

дисперсия погрешности вычислений будет равна сумме компонент:

, (11)

где - дисперсия погрешности аппроксимации; 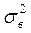- дисперсия вычислительной погрешности; σ2т - дисперсия трансформационной погрешности; - дисперсия параметрической погрешности;

- дисперсия динамической погрешности.

Погрешность аппроксимации зависит от структуры алгоритма, т. е. выбранного численного метода решения задач. При известном законе распределения плотности вероятностей максимальная вероятная ошибка вычисления может быть оценена по формуле:

,

где g - параметр, зависящий от закона распределения и задаваемой вероятности оценки погрешностей.

Трансформационная погрешность σ²_т определяется, в основном, разрядностью аналого-цифрового преобразователя (АЦП) или же точностью вводимых данных. Погрешность исходных данных пересчитывается к выходной величине, рассчитываемой по формуле:

у = φ (х), (14)

где у – расчетная выходная величина, х – входная информация, j(х) - алгоритм вычисления.

Вычислительная погрешность σ²_в зависит от количества вычислительных операций в алгоритме решения задачи, разрядности ЭВМ, а также формы представления данных и масштабирования данных. Вычисления можно представить совокупностью отдельных вычислительных операций. Дисперсия погрешности одной вычислительной операции при равномерном законе распределения погрешности может быть оценена по формуле:

, (17)

где Dy – цена младшего разряда расчетной выходной величины.

 

Если в программе реализуется N _в вычислительных операций, тогда дисперсия погрешности вычислений будет равна:

σ²_в = N _в σ²₀₁. (18)

 

Параметрическая погрешность σ² _псвязана с погрешностями квантования констант вычислительных алгоритмов. Зависит от разрядности и формы представления чисел, имеет равномерный закон распределения. Дисперсия параметрической погрешности рассчитывается по формуле:

, (19)

где Dk – абсолютная погрешность хранения констант.

 

Динамическая погрешность σ²_д обусловлена конечной продолжительностью времени выполнения вычислений и, следовательно, с запаздыванием выдачи управляющих воздействий (решения задачи), в общем случае, на k – тактов. Величина абсолютной динамической погрешности определяется формулой:

D д (n D t) = y (n D t) - j(x (n – k)D t),

где D t – шаг квантования; n D t – момент определения погрешности.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: