 |
Характеристика классической сети Петри. Свойства сетей Петри.
|
|
|
|
для моделирования динамических вычислительных процессов могут использоваться сети Петри. Сети Петри позволяют строить модели сложных систем в виде соответствующих структур, образованных из элементов двух типов – событий и условий. В свою очередь в сетях события и условия представлены в виде двух непересекающихся подмножеств, а именно множеством позиций и множеством переходов. Атрибутивная сеть является подклассом сетей Петри [10].
Формально атрибутивная сеть представляет собой набор
N = (P, T, F, W, M0) (1)
где P – множество элементов сети, называемых позициями;
T – множество элементов сети, называемых переходами;
F _ P? T?? T? P – отношение инцидентности;
W: P ® N – функция кратности дуг;
M0: P ® N – функция начальной разметки.
В графическом представлении сетей переходы представляются “барьерами”, а позиции – кружками (рис.24).
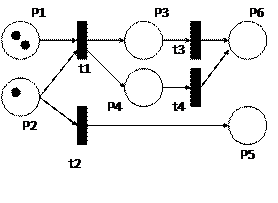 |
Рисунок 24 – Графическое представление сети Петри
В соответствии с выражением (1) P условия-позиции и события-переходы связаны отношением непосредственной зависимости (причинно-следственной связи), которое изображается с помощью направленных дуг, ведущих из позиций в переходы и из переходов в позиции. При этом функция W сопоставляет каждой дуге число n > 0 (кратность дуг). Позиции, из которых ведут дуги на данный переход, называются его входными позициями. Позиции, на которые ведут дуги из данного перехода, называются его входными позициями. Так, в сети на рис. 24 позиции p1 и p2 являются входными для перехода t1, а места p3 и p4 – выходными. В этом же примере позиция p2 является выходным одновременно для двух переходов t1 и t2, а позиции p6 являются входным одновременно для двух переходов – t3 и t4.
|
|
|
Выполнение условия изображается разметкой соответствующей позиции, а именно помещением числа n или n фишек (маркеров) в эту позицию, где n > 0. Функция M сопоставляет каждой позиции p Î P некоторое число
M0(p) Î N (разметка позиции) (2)
Динамика поведения моделируемой системы отражается в функционировании сети в виде совокупности локальных действий, которые называются срабатыванием переходов. Они соответствуют реализациям событий и приводят к изменению разметки позиций, т.е. к локальному изменению условий в системе.
Переход может сработать, если выполнены все условия реализации соответствующего события. Срабатывание перехода – неделимое действие, изменяющее разметку его входных и выходных позиций следующим образом: из каждой входной позиции изымается по одной фишке, а в каждую входную позицию добавляется по одной фишке. Тем самым реализация события, изображенного переходом, изменяет состояние (емкость) непосредственно связанных с ним условий так, что емкость предусловий, вызвавших реализацию этого события, уменьшается, емкость постусловий на которые оно влияет, увеличивается. Переход t1 на рис.24 может сработать, так как обе его входные позиции p1 и p2 содержат фишки, а после срабатывания t1 разметка его входных и выходных позиций изменяется так, как показано на рис.25.
 |
Рисунок 25 – Изменение маркировок после срабатывания перехода t1
Если два перехода (и более), например t3 и t4 на рис.25, могут сработать и они не имеют общих входных позиций, то их срабатывания являются независимыми действиями, осуществляемыми в любой последовательности или параллельно. Таким образом, в сети моделируется параллелизм событий (рис. 26).
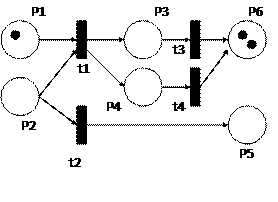 |
Рисунок 26 – Параллельное срабатывание переходов t1, t2
Если несколько переходов могут сработать и имеют общую входную позицию (как переходы t1 и t2 на рис.24), то срабатывает только один (любой) из них. При этом может оказаться, что, сработав, этот переход лишит возможности сработать другие переходы (рис.27). Таким образом, в сети моделируется конфликт между событиями, когда реализация одного из них может исключить возможность реализации других. Аналогичный конфликт возникает в том случае, когда несколько переходов могут сработать и они имеют общие выходные позиции t3 и t4.
|
|
|

Рисунок 27 – Моделирование конфликтов между событиями
В процессе функционирования сети происходит смена разметок позиций, как результат срабатывания ее переходов. Сеть останавливается, если ни один из ее переходов не может сработать.
Таким образом, атрибутивные сети формализуют понятие абстрактной асинхронной системы – динамической структуры из событий и условий.
Для анализа сетей используются понятия определенных свойств сетей:
-ограниченности позиций сети и сети в целом;
-безопасности позиции сети и сети в целом;
-консервативности сети;
-живости и мертвости переходов;
-живости сети;
-устойчивости переходов и сети в целом;
При решении практических задач моделирования сетями дискретных систем производится анализ сетевых моделей систем, в частности пакетом Design/IDEF моделей IDEF0/CPN, на предмет обладания данными свойствами [11]. Результаты анализа позволяют судить о свойствах поведения моделируемой системы.
Таким образом, с формальной точки зрения IDEF/CPN – модель представляет собой атрибутивную или иерархическую раскрашено–предикатную сеть.
|
|
|


