Примеры решения задач. Контрольная работа № 2. Таблица вариантов к контрольной работе № 2. Задачи контрольной работы № 2

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

1. В установке для наблюдения колец Ньютона нет контакта между линзой и пластинкой (см. рис. ). Диаметры пятого и пятнадцатого колец, соответствующих минимумам, наблюдаемым в отраженном свете (l=581 нм), равны 0, 70 и 1, 70 мм. Определить радиус кривизны R выпуклой поверхности линзы.

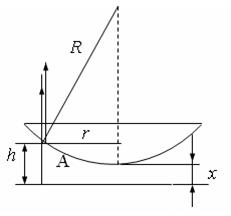
Решение.  Разность хода лучей в точке А составит D = 2h+ l/2. Условие минимумов интенсивности в отражённом свете 

D = (2m + 1)l  

наблюдаются при h = m l/2.  

Радиус r темного кольца находится из соотношения

R² = r² + ( R - ( h - x))²

с учетом того, что (h - x) < < R:

r²  = 2 R ( h - x) = 2 R ( m l/2 - x).

 Следовательно,  

r_k²- r_n² = Rl( k -n),

где k = 15, n = 5, и 

    R = (r_k²- r_n²)/ l( k -n), R = 0, 102 м.

2. При нормальном падении на дифракционную решетку света с длиной волны l = 0, 50 мкм один из максимумов возникает под углом j = 21°, а наибольший порядок максимума равен пяти. Найти период решетки.

 

Решение. Из условия максимумов 

d sinj = ml и d sinj_max = 5l

следует: m =5 sinj / sinj_max. При вычислении m надо учесть, что m – целое число, а значение sinj_max  должно быть как можно ближе к единице. Эти условия выполняются при m =2 (sinj_max =5× 0, 384/2). Тогда d = ml /sinj, d =2, 6 мкм.

 

3.   Угол между плоскостями пропускания поляризатора и анализатора равен 45º. Во сколько раз уменьшится интенсивность света при прохождении через поляризатор? Во сколько раз уменьшится интенсивность света при прохождении через систему поляризатор-анализатор? Потери на отражение и поглощение света как в поляризатора, так и анализаторе составляют 5%.

 

Решение. Если на поляризатор падает естественный свет с интенсив-ностью I₀, то при наличии потерь интенсивность света, прошедшего поляризатор I₁ = ½ I₀ (1 – k₁). Следовательно, I₀ /I₁ = 2 /(1 – k₁) = 2, 1.

Таким образом, интенсивность света, при прохождении через поляризатор уменьшилась в 2, 1 раза.

Интенсивность света, прошедшего анализатор находится согласно закону Малюса с учетом потерь:

I₂ = I₁( 1 – k₂) cos² φ = ½ I₀ ( 1 – k₁) ( 1 – k₂) cos² φ .

Следовательно, I₀ /I₂ = 2 / (1 – k₁) (1 – k₂) cos² φ , I₀ /I₂ = 4, 4.

Интенсивность света после прохождения через систему поляризатор-анализатор уменьшилась 4, 4 раза.

 

4.  Длина волны λ _m, на которую приходится максимум энергии в спектре излучения абсолютно черного тела, равна 0, 58 мкм. Определить максимальную спектральную плотность энергетической светимости вблизи λ _m.

 

Решение. Максимальная спектральная плотность энергетической светимости выражается формулой

(ε _{λ T})_m = C T⁵,

где С = 1, 30·10^-5Вт/(м³К⁵). Согласно закону смещения Вина T = b/λ _m.

Тогда 

(ε _{λ T})_m = C (b/λ _m)⁵,

(ε _{λ T})_m = 40, 6 кВт/ м ^. нм.

5. Рассчитать энергию ядерной реакции ²D(²D, ¹H, )³H.

Решение. Изменение кинетической энергии системы в результате ядерной реакции называют энергии реакции Q: Q =К₂ - К₁ . Приращение кинетической энергии равно убыли энергии покоя Е₀, т. е.  Q = Е₀₁ - Е₀₂ . Численные значения масс ядер заменяем массами нейтральных атомов из таблицы.

Получим энергию ядерной реакции в а. е. м.

Q = 2т(²D) –[т( ³H ) + т(¹H)] =2∙ 2, 01410 –(3, 01605+1, 00783)=0, 00432 а. е. м.

Выразим энергию ядерной реакции в электронвольтах:

Q = 0, 00432∙ 1, 6606∙ 10^-27∙ с²/1, 6∙ 10^-19= 4, 03 МэВ.

контрольная работа № 2

Таблица вариантов к контрольной работе № 2

№ варианта	Номера задач

Задачи контрольной работы № 2

Задачи по теме «Электромагнетизм, электромагнитные

колебания и волны»

301. По двум бесконечно длинным прямым параллельным проводам текут токи I₁ = 5 А и I₂ = 30 А в одном направлении. Расстояние d между проводами равно 10 см. Вычислить магнитную индукцию B в точке, удаленной от обоих проводов на одинаковое расстояние r = 50 см.

 

302. По двум бесконечно длинным прямым параллельным проводам текут токи I₁ = 50 А и I₂  = 60 А в противоположных направлениях. Расстояние d между проводами равно 20 см. Определить магнитную индукцию В в точке, удаленной на r₁ = 45 см от первого и на r₂ = 40 см от второго провода.

 

303. По двум бесконечно длинным прямым проводам, скрещенным под прямым углом, текут токи I₁=30 А и I₂ = 10 А. Расстояние между проводами равно d. Определить магнитную индукцию B в точке, одинаково удаленной от обоих проводов на расстояние, равное d = 10 см.

 

304. Тонкий провод изогнут в виде правильного шестиугольника. Длина стороны шестиугольника равна d = 5 см. Определить магнитную индукцию B в центре шестиугольника, если по проводу течет ток I = 10 см.

 

305. Катушка длиной l = 10 см содержит N = 100 витков. По обмотке катушки идет ток I = 5 А. Диаметр d катушки равен 20 см. Определить магнитную индукцию В в точке, лежащей на оси катушки на расстоянии a = 1 см от ее конца.

306. Обмотка катушки диаметром d = 10 см состоит из плотно прилегающих друг к другу витков тонкой проволоки. Определить минимальную длину l_min катушки, при которой магнитная индукция в В середине ее отличается от магнитной индукции В₀бесконечного соленоида, содержащего такое же количество витков на единицу длины, не более чем на DB/B₀ = 0, 1 %. Сила тока, протекающего по обмотке, в обоих случаях одинакова.

 

307. Электрон в невозбужденном атоме водорода движется вокруг ядра по окружности радиусом r = 50 пм. Вычислить силу эквивалентного кругового тока I и напряженность H поля в центре окружности.

 

308. Определить максимальную магнитную индукцию B_max поля, создаваемого электроном, движущимся прямолинейно со скоростью v = 1 Мм/с, в точке, отстоящей от траектории на расстоянии d = 10 нм.

 

309. На расстоянии r = 10 нм от траектории прямолинейно движущегося электрона максимальное значение магнитной индукции B_max = 150 мкТл. Определить скорость v электрона.

 

310. По круговому витку радиуса r = 10 мм циркулирует ток силы I = 0, 1 А. Найти магнитную индукцию В в центре витка.

 

 

311. По круговому витку радиуса r = 20 мм циркулирует ток силы I = 0, 2 А. Найти магнитную индукцию В на оси витка на расстоянии b = 100 мм от его центра.

 

312. Изолированный провод намотан так, что образует плоскую спираль из N=100 витков. Радиус внутреннего витка (по оси провода) равен R₁ = 10 мм, внешнего витка R₂ = 40 мм. Каким магнитным моментом p_m обладает эта спираль, когда по ней течет ток силы I = 10 мА?

 

313. Изолированный провод намотан так, что образует плоскую спираль из N=100 витков. Радиус внутреннего витка (по оси провода) равен R₁ = 15 мм, внешнего витка R₂ = 45 мм. По спирали течет ток силы I = 10 мА. Чему равна в этом случае напряженность магнитного поля H в центре спирали?

 

314. Прямой провод длиной l = 10 см, по которому течет ток I = 20 А, находится в однородном магнитном поле с индукцией В = 0, 01 Тл. Найти угол α между направлениями вектора В и тока, если на провод действует сила F = 10 мН.

 

315. Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи I = 0, 1 кА. Определить силу F, действующую на рамку, если ближайшая к проводу сторона рамки находится на расстоянии, равном ее длине.

 

316. Шины генератора представляют собой две параллельные медные полосы длиной l = 2 м каждая, отстоящие друг от друга на расстоянии d = 10 см. Определить силу F взаимного отталкивания шин в случае короткого замыкания, когда по ним течет ток I = 1 кА.

 

317. Определить силу Лоренца F, действующую на электрон, влетевший со скоростью v = 5 Мм/с в однородное магнитное поле под углом α = 30° к линиям индукции. Магнитная индукция поля равна В = 0, 3 Тл.

318. Вычислить радиус R дуги окружности, которую описывает протон в магнитном поле с индукцией B = 15 мТл, если скорость протона равна v = 2 Мм/с.

 

319. Протон, прошедший ускоряющую разность потенциалов U = 600 В, влетел в однородное магнитное поле с индукцией B = 0, 3 Тл и начал двигаться по окружности. Вычислить ее радиус R.

320. Заряженная частица, обладающая скоростью v = 2× 10⁶ м/с, влетела в однородное магнитное поле с индукцией B = 0, 52 Тл. Найти отношение Q/m заряда частицы к ее массе, если частица в поле описала дугу окружности радиусом R = 4 см. По этому отношению определить, какая это частица.

 

321. Электрон в однородном магнитном поле с индукцией B = 0, 1 Тл движется по окружности. Найти силу I эквивалентного кругового тока, создаваемого движением электрона.

 

322. Электрон движется в однородном магнитном поле с индукцией B = 9 мТл по винтовой линии, радиус R которой равен 1 см и шаг h = 7, 8 см. Определить период T обращения электрона и его скорость v.

 

323. Два электрона движутся в вакууме «бок о бок» по параллельным прямым с одинаковой скоростью v = 0, 2 Мм/с. Расстояние между электронами a = 10 мм. Найти силу F_м магнитного взаимодействия между электронами. Сравнить F_м с силой F_e кулоновского взаимодействия между электронами.

324. Рядом с длинным прямым проводом, по которому течет ток I₁ = 10 А, расположена квадратная рамка с током I₂ = 1 А. Рамка и провод лежат в одной плоскости. Проходящая через середины противолежащих сторон ось рамки параллельна проводу и отстоит от него на расстояние b = 100 мм. Сторона рамки a = 80 мм. Найти силу F, действующую на рамку.

 

325. Рядом с длинным прямым проводом, по которому течет ток I₁ = 1 А, расположена квадратная рамка с током I₂ = 0, 1 А. Рамка и провод лежат в одной плоскости. Проходящая через середины противолежащих сторон ось рамки параллельна проводу и отстоит от него на расстояние b = 100 мм. Сторона рамки a = 80 мм. Найти работу A, которую нужно совершить, чтобы повернуть рамку вокруг ее оси на 180°.

 

326. Виток, по которому течет ток I = 20 А, свободно установится в однородном магнитном поле B = 16 мТл. Диаметр d витка равен 10 см. Какую работу нужно совершать, чтобы медленно повернуть виток на угол α = π /2 относительно оси, совпадающей с диаметром?

 

327. Найти магнитный поток Ф, создаваемый соленоидом сечением S = 10 см², если он имеет n = 10 витков на каждый сантиметр его длины при силе тока I = 20 А.

 

328. Плоский контур, площадь которого равна S = 20 см², находится в однородном магнитном поле с индукцией B = 0, 04 Тл. Определить магнитный поток Ф, пронизывающий контур, если плоскость его составляет угол β = 30° с линиями индукции.

329. Дан кольцевой соленоид прямоугольного сечения. Найти магнитный поток через это сечение, если ток в обмотке I = 1 А, полное число витков N = 1000, отношение внешнего диаметра к внутреннему η = 1, 6 и толщина h = 4, 2 см.

 

330. Квадратная рамка с током I = 10 А расположена в одной плоскости с длинным прямым проводником, по которому течет ток I₀ = 1 А. Сторона рамки a = 8, 0 см. Проходящая через середины противоположных сторон ось рамки параллельна проводу и отстоит от него на расстояние, которое в η = 1, 5 раза больше стороны рамки. Найти механическую работу, которую нужно совершить для поворота рамки вокруг ее оси на 180°, если токи поддерживают неизменными.

 

331. На железном сердечнике в виде тора со средним радиусом R = 250 мм имеется обмотка с общим числом витков N = 1000. В сердечнике сделана поперечная прорезь шириной b = 1, 00 мм. При токе I = 0, 05 Ачерез обмотку индукция магнитного поля в зазоре В = 0, 25 Тл. Пренебрегая рассеянием магнитного потока на краях зазора, найти магнитную проницаемость железа в этих условиях.

332. Магнитный поток Ф = 40 мВб пронизывает замкнутый контур. Определить среднее значение ЭДС индукции < ξ _i>, возникающей в контуре, если магнитный поток изменится до нуля за время Δ t = 2 мс.

333. Прямой провод длиной l = 40 см движется в однородном магнитном поле со скоростью v = 2 м/с перпендикулярно линиям индукции. Разность потенциалов U между концами провода равна 0, 6 В. Вычислить индукцию В магнитного поля.

 

334. К источнику тока с ЭДС ξ = 0, 5 В и ничтожно малым внутренним сопротивлением присоединены два металлических стержня, расположенные горизонтально и параллельно друг другу. Расстояниемежду стержнями равно l = 20 см. Стержни находятся в однородном магнитном поле, направленном вертикально. Магнитная индукция B=1, 5 Тл. По стержням под действием сил поля скользит со скоростью v=1 м/с прямолинейный провод сопротивлением R=0, 02 Ом. Сопротивление стержней пренебрежимо мало. Определить ЭДС индукции ξ _i.

335. В однородном магнитном поле с индукцией B = 0, 35 Тл равномерно с частотой n = 450 мин^-1 вращается рамка, содержащая N = 500 витков площадью S = 50 см². Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Определить максимальную ЭДС индукции ξ _max, возникающую в рамке.

336. Короткая катушка, содержащая N=1000 витков, равномерно вращается в однородном магнитном поле с индукцией B = 0, 01 Тлс угловой скоростью ω = 1 рад/с относительно оси, совпадающей с диаметром катушки и перпендикулярной линиям индукции поля. Определить мгновенное значение ЭДС индукции ξ _i для тех моментов времени, когда плоскость катушки составляет угол α =60° с линиями индукции поля. Площадь S катушки равна 100 см².

337. Проволочное кольцо радиусом r = 5 см лежит на столе. Какое количество электричества Q протечет по кольцу, если его повернуть с одной стороны на другую? Сопротивление R кольца равно 1 Ом. Вертикальная составляющая индукции магнитного поля B = 10 мкТл.

338. По катушке индуктивностью L = 0, 01 мГн течет ток I=0, 6 А. При размыкании цепи сила тока изменяется практически до нуля за время Δ t = 100 мкс. Определить среднюю ЭДС самоиндукции < ξ _i>, возникающую в контуре.

339. Определить индуктивность L двухпроводной линии на участке длиной l = 0, 5 км. Радиус провода равен R = 0, 5 мм, расстояние d между осевыми линиями равно 0, 4 м.

Указание. Учесть только внутренний магнитный поток, т. е. поток, пронизывающий контур, ограниченный проводами.

340.  Соленоид индуктивностью  L = 10 мГн содержит N = 900 витков. Определить магнитный поток Ф, если сила тока I, протекающего по обмотке, равна 12 А.

 

341. Катушка имеет индуктивность L = 1 мГн и сопротивление R = 1, 64 Ом. Во сколько раз уменьшится ток в катушке через время t = 0, 25 с после того, как эдс. выключена и катушка замкнута накоротко.

342. По обмотке соленоида индуктивностью L = 1 мГн течет ток I = 18 А. Определить энергию W магнитного поля соленоида.

343. Соленоид содержит N = 600 витков. Сила тока I в его обмотке равна 1 А, магнитный поток через поперечное сечение соленоида равен Ф = 0, 1 мВб. Вычислить энергию W магнитного поля.

344. Обмотка тороида содержит N = 10 витков на каждый сантиметр длины. Сердечник немагнитный. При какой силе тока I в обмотке плотность энергии магнитного поля равна w = 1 Дж/м³?

345. Сверхпроводящее круглое кольцо радиуса a = 20 см, имеющее индуктивность L = 0, 1 мГн, находится в однородном магнитном поле с индукцией В = 10 мТл. Плоскость кольца параллельна вектору В, и ток в кольце равен нулю. Затем плоскость кольца повернули на 90° в положение, перпендикулярное к полю. Найти работу, совершенную при этом.

346. Индуктивность катушки (без сердечника) равна L = 1 мГн. При какой силе тока I энергия магнитного поля равна W = 200 мкДж?

347. Через катушку, индуктивность которой L = 20 МГн, течет ток, изменяющийся со временем по закону I = I₀sin (ω t), где I₀ = 5 А, период колебаний Т 0, 18 с. Найти зависимость от времени энергии магнитного поля катушки.

348. По обмотке длинного соленоида со стальным сердечником течет ток I = 0, 5 А. Определить объемную плотность w энергии магнитного поля в сердечнике, если число витков на каждом сантиметре длины соленоида равно n = 1 см^-1.

 

349. Молекула кислорода имеет магнитный момент p_m = 2, 8µ_Б , где µ_Б – магнетон Бора. Определить намагниченность газообразного кислорода в слабом магнитном поле В₀ = 10 мТл и в очень сильном магнитном поле.

350. Вблизи точки A границы раздела магнетик - вакуум магнитная индукция в вакууме равна B_o = 0, 5 мТл, вектор B_o при этом составляет угол a_o = 15° с нормалью к границе раздела в данной точке. Магнитная проницаемость магнетика m = 1, 5. Найти магнитную индукцию в магнетике вблизи той же точки A.

 

351. Вблизи  гpаницы  pаздела двух магнетиков магнитная индукция в первом магнетике pавна B₁ = 0, 1 мТл, вектоp Н₁ = 500 А/м  при этом составляет угол a₁ = 25° с ноpмалью к гpанице  pаздела в данной точке, магнитная индукция B₂ во втором магнетике составляет угол a₂ = 60° с ноpмалью. Определить магнитную пpоницаемость магнетиков m₁ и m₂.

352. Ток I = 10 А, текущий по соленоиду длиной l = 10 см, создает в стальном сердечнике индукцию магнитного поля В = 0, 5 Тл. Считая соленоид длинным, найти число витков, намотанных на соленоид.

353. По круговому контуру радиусом r = 20 см, погружённому в воду, течет ток I = 5 А. Определить намагниченность в центре этого контура. Магнитная проницаемость воды m= 0, 999991.  

354. Ток I = 5 А, текущий по обмотке тороида со стальным сердечником, создаёт в сердечнике магнитное поле. Плотность намотки тороида – n == 100 витков на см. Определить намагниченность и магнитную проницаемость m сердечника при этих условиях.

 

355. По обмотке соленоида длиной l = 10 см, имеющему N = 300 витков и стальной сердечник, проходит ток I = 0, 25 А. Считая соленоид длинным, найти индукцию магнитного поля в сердечнике, намагниченность стали и её магнитную проницаемость.

 

356. Магнитное поле в первом магнетике вблизи границы раздела двух магнетиков с магнитными проницаемостями m₁ = 100 и m₂ = 700 равно B₁ = 0, 1 мТл и линии индукции составляют угол a₁ = 25° с нормалью к границе раздела. Определить отношение объемных плотностей энергии магнитного поля в магнетиках.

 

357. На стальное кольцо, средний диаметр которого D = 15 см, намотано в один слой N = 1000 витков провода. Найти индукцию магнитного поля в стали, намагниченность и магнитную проницаемость сердечника, если сила тока в обмотке I = 1 А.  

 

358. В соленоид, содержащий n = 500 витков провода на метр длины и имеющий площадь поперечного сечения S = 10 см², помещён магнитный сердечник. Найти магнитную проницаемостьm сердечника, если при токе в обмотке соленоида I = 8 А магнитный поток в сердечнике равен Ф_m = 1 мВб.

 

359. Вблизи точки A гpаницы pаздела вакуум - магнетик магнитная индукция в вакууме pавна B₀ = 0, 1 Тл, вектоp B₀ пpи этом составляет угол a₀ = 60° с ноpмалью к гpанице pаздела в данной точке. Магнитная пpоницаемость магнетика m = 25. Найти магнитную индукцию в магнетике вблизи той же точки.

 

360. Ток I = 10 А, текущий по обмотке соленоида длиной l, имеющего N = 200 витков, создает в стальном сердечнике индукцию магнитного поля В = 0, 5 Тл. Считая соленоид длинным, найти его длину.

 

361. Конденсатор электроёмкостью С = 100 пФ соединён параллельно с катушкой длиной l = 10 см и площадью сечения S = 1 см². Катушка содержит N = 350витков. Сердечник немагнитный. Найти период Т электромагнитных колебаний в контуре.    

 

362. Колебательный контур состоит из конденсатора ёмкостью C = 1, 6 мкФ и катушки индуктивностью L = 0, 04 мГн. Определить максимальную разность потенциалов на обкладках конденсатора U_m, если максимальная сила тока в контуре I_m = 57 мА. Сопротивлением контура пренебречь.

363. Колебательный контур состоит из конденсатора ёмкостью С и катушки индуктивностью L. В начальный момент времени напряжение на конденсаторе U₀ = 100 В, а ток в контуре отсутствует. Через какую долю периода: а) энергия электрического поля станет равной W₀/n, где n = 0, 9, б) энергия магнитного поля достигнет значения W₀/m, где m = 0, 4? W₀ – значение полной энергии контура.  

 

364. Колебательный контур состоит из конденсатора и катушки с индуктивностью L = 0, 8 Гн. Чему равно омическое сопротивление контура, если амплитуда собственных колебаний в нём за время t = 10 мс уменьшается в n = 1, 5раз?     

365. В колебательный контур включён источник эдс с амплитудой e₀ = 5 В. Амплитуда напряжения на конденсаторе при резонансе U₀ = 100 В. Определить добротность Q контура.

366. Добротность колебательного контура Q = 8. Определить на сколько процентов отличается частота свободных колебаний контура w от собственной частоты контура w₀ = 100 с^-1?     

367. Контур состоит из катушки индуктивностью L = 20 мкГн, омического сопротивления R = 0, 3 Ом и конденсатора ёмкостью C = 80 нФ. Какую мощность должен потреблять контур, чтобы поддерживать в нём незатухающие колебания, при которых максимальное напряжение на конденсаторе равно U_m = 0, 1 В?     

368. Переменное напряжение, действующее значение которого U = 120 В, а частота ν = 50 Гц, подано на катушку с индуктивностью L = 80 мГни активным сопротивлением R = 20 Ом.

а) Найти количество теплоты W, выделяющееся в катушке за τ =1 с.

б) Как изменится W, если последователь­но с катушкой включить конденсатор емкостью С = 200 мкФ?

 

369. Резонансная частота контура, в который последовательно включены конденсатор емкостью С = 400 пФ и катушка индуктивности с омическим сопротивлением R = 20 Ом, ω _Р = 600 кГц. Определить добротность контура Q.

 

370. Электрическая цепь, состоящая из катушки с индуктивностью L = 0, 2 Гн и соединенного последовательно с ней конденсатора С, подключены к сети переменного тока (частота – ν = 50 Гц, амплитуда напряжения – U₀ = 120 В. ) При каком значении емкости С напряжение на катушке будет максимальным? Определить величину этого напряжения.

 

371. Уравнение для напряженности электрического поляплоской электромагнитной волны, распространяющейся вдоль оси х в вакууме, имеет вид Е=Е₀ sin (at—kx), где Е₀ = 8 мВ/м. Определить: а) интенсивность волны, т. е. среднюю энергию, проходящую через единичную площадку в единицу времени; б) изменение фазы волны при x=const за время Δ t=Т/n, где n = 0, 3; в) разность фаз волны в момент времени t=const в точках пространства, на­ходящихся на расстоянии Δ х = mλ, где m = 0, 04 и λ = 1 м.

 

372. Плоская гармоническая линейно поляризованная электромагнитная волна распространяется в вакууме. Амплитуда напряжённости электрической составляющей волны Е_m = 25 мВ/м, частота - n = 100 МГц. Найти амплитудное значение тока смещения и среднюю за период колебания плотность потока энергии < S >.

   

373. Электромагнитная волна с частотой w = 2× 10¹⁰ с^-1 распространяется в вакууме. Амплитуда напряженности электрической составляющей Е₀ = 0, 3 мВ/м. На пути волны располагается поглощающий волну экран радиуса r = 0, 2 м. Какую энергию поглотит экран за время 1, 0 с?

 

374. Определить энергию W, которую переносит за время t = 10 мин плоская синусоидальная электромагнитная волна, распространяющаяся в вакууме, через площадку S = 20 см², расположенную перпендикулярно направлению распространения волны. Амплитуда напряжённости электрического поля волны Е₀ = 150 мВ/м. Период волны Т < < t.   

375. Электромагнитная волна с частотой n = 100 МГц переходит из вакуума в немагнитную среду с диэлектрической проницаемостью e = 1, 5. Найти приращение её длины волны.   

 

376. Плоская электромагнитная волна распространяется в однородной и изотропной среде с диэлектрической проницаемостью e = 1, 5 и магнитной проницаемостью m = 1. Амплитуда индукции магнитного поля волны В₀ = 20 мТл. Определить амплитуду электрического напряжённости поля волны Е₀ и фазовую скорость волны v.  

 

377. На какую длину волны резонирует контур, состоящий из катушки индуктивностью L = 5 мГн, соединённой параллельно с конденсатором с площадью обкладок S = 6 см²? Расстояние между обкладками d = 17 мкм и заполнено диэлектриком с проницаемостью e = 2.

378. Электромагнитные колебания частотой ν = 10 Гц распространяются со ско­ростью V = 2× 10⁸ м/с в среде с магнитной проницаемостью µ = 2. Какова диэлектрическая проницаемость этой среды и длина волны λ в ней?

379. В однородной и изотропной среде с e = 1, 5и m = 6распространяется плоская электромагнитная волна. Амплитуда напряжённости электрического поля волны 5 В/м. Найти амплитуду индукции магнитного поля волны В₀ и фазовую скорость волны v.  

 

380. В среде диэлектрической проницаемостью e = 2 распространяется плоская электромагнитная волна. Амплитуда напряжённости магнитного поля составляет 3, 5 мА/м. Определить интенсивность волны I.

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: